基于APOS理論下的初中“函數”概念的教學設計

李璐華

【摘要】 筆者在本文中以北師大版八年級上冊第4章第1節《函數》一課為例，淺談在APOS視角下的數學概念教學設計。

【關鍵詞】 APOS理論 初中 函數概念 教學設計

【中圖分類號】 G633.6 【文獻標識碼】 A 【文章編號】 1992-7711（2015）02-86-01

數學概念是形成數學知識體系、構建數學理論大廈的基石，是導出數學定理和數學法則的邏輯基礎，是進行判斷、推理的依據，是形成數學知識體系的基本要素。數學課程標準在課程目標中指出，要讓學生獲得必要的基礎知識和基本技能，理解基本的數學概念、數學本質。但是目前，在初中數學概念教學中，有兩種傾向：一是大多數教師習慣采用的概念同化教學方式，這種傳統的教學方式偏重概念的邏輯結構，學生對數學概念的學習是靠教師直接或間接的代替而進行的塊體驗、抽象，容易造成一部分中等生和學困生對概念理解不深；二是進行大量“去數學化”的實驗探究，忽略了對思維的鍛煉，結果整節課下來，學生對概念的內涵不能了解透徹。

1 教學背景

《函數》是2013北師大版8年級數學上冊第4章第1節的內容。學生七年級上冊學習了《用字母表示數》，體會了字母表示數的意義；在七年級下冊已學習了《變量之間的關系》，對變量間互相依存的關系有了一定的認識，為學習《函數》知識打下了一定的基礎。教材中從具體實際問題的數量關系和變化規律中抽象出函數的概念，然后讓學生分析了大量的實際問題，感受表示兩個變量之間關系的方式是多樣的，如列表法，圖像法，解析式法，但都有著共性：其中一個變量依賴于另一個變量。函數是研究現實世界變化規律的一個重要模型，對它的學習一直是初中階段數學學習的一個重要內容。本節內容讓學生初步體會函數的概念，為后續學習打下基礎。同時，函數的學習可以使學生體會到數形結合的思想方法，感受事物是相互聯系和規律的變化。

2 教學目標

知識與技能目標：初步掌握函數概念，能判斷兩個變量之間的關系是否可以看作函數；根據兩個變量之間的關系式，給定其中一個變量的值相應的會求出另一個變量的值；會對一個具體實例進行概括抽象成為函數問題。

3 教學重難點

教學重點：掌握函數概念，會判斷兩個變量之間的關系是否可以看作函數。

教學難點：理解函數的概念，能把實際問題抽象概括成函數問題。

4 APOS理論下的教學過程

4.1第1階段：活動階段（Action）

[活動1]問題1：游樂園中的摩天輪

（1）如果你坐在摩天輪上，隨著時間的變化，你離開地面的高度是如何變化的？

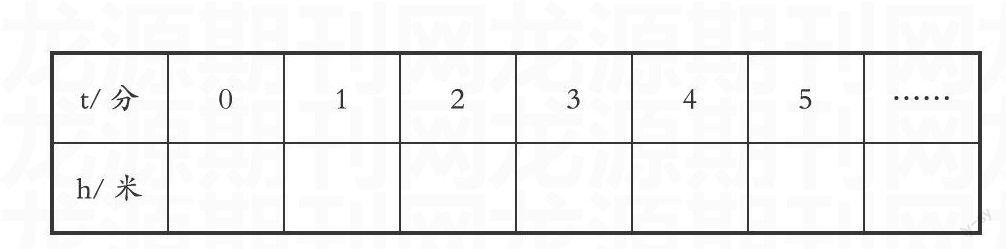
右上圖反映了旋轉時間t（分）與摩天輪上一點的高度h（米）之間的關系。

（2）從圖象上，你能讀出哪些信息？

（3）對于給定的時間t，相應的高度h確定嗎？

根據右上圖進行填表（如表1所示）：

首先由學生分組討論完成，然后相互交流。

4.2第2階段：過程階段（Process）

[活動2]探討：以上三個問題中的共同點是什么？不同點又是什么？

生：相同點是，這三個問題中都研究了兩個變量。不同點是，在第一個問題中，是以圖象的形式表示兩個變量之間的關系；第二個問題中是以表格的形式表示兩個變量間的關系；第三個問題是以關系式來表示兩個變量間的關系的。

4.3第3階段：對象階段（Object）

[活動3]歸納揭示函數的概念：

一般地，在某個變化過程中，有兩個變量x和y，如果給定一個x值，相應地就確定了一個y值，那么我們稱y是x的函數，其中x是自變量，y是因變量。

歸納出函數概念后，留幾分鐘時間給學生消化理解概念，并提出自己不理解的地方，教師再提出：

（1）上面問題中的自變量和因變量是什么？

（2）你能舉出生活中是函數的例子嗎？

（3）你是怎樣理解“確定”這兩個字的含義的？

學生分組討論交流，教師點評總結：理解函數概念應把握三點，一個變化過程；兩個變量；對于一個變量的每一個值，另一個變量都有唯一的值與它對應，即是一種對應關系。判斷兩個量是否具有函數關系就以這三點為依據。

4.4第4階段：圖式階段（Scheme）

通過前三個階段，學生對函數的概念以及常用的三種表示方式有了一定的理解。本階段主要通過練習鞏固，讓學生根據所學的新概念，自主建立函數的心理圖式，對兩個變量之間的關系、函數的概念以及函數的三種表示法構建出自己的“圖式網”；進而，讓學生知道本課主要學習內容是什么，如何應用來解決問題，這節課學到了什么知識。

5 APOS理論應用于概念教學的幾點思考

5.1理解數學，于過程中生成概念

“函數”的概念在歷史上經歷了二百多年、三次修正的過程，才歸納、總結、抽象、概括為現行初中課本中函數的概念，“函數”概念是初中數學最抽象、學生最難學的內容。因此，北師大版教材的編者在編寫教材時，也從分考慮到讓學生參與函數概念形成的全過程，把傳授知識與培養能力兩個目標結合起來。

5.2理解學生，從過程中體驗概念

學生是學習過程的主體，“APOS理論”強調學生的學習是一個主動建構的過程，每個學習者都以自己原有的認知結構為基礎對新的信息進行編碼，構建自己的理解；函數是學生進入初中以來第一次碰到的內容，且概念本身具有高度的抽象性，學生理解和熟悉概念相當的困難。

5.3理解教學，在操作中建構概念

學生對于數學概念的掌握不可能一蹴而就，而是一個從感知到掌握的循序漸進的過程。特別是“函數”這個貫穿于整個中學階段的核心概念，它的教學更應該采用螺旋式的循序漸進的方式。“APOS理論”揭示了概念形成的規律性和學生的認知規律。在這個教學設計中，通過幾個與函數相關的生活中的實例來歸納它們的共同本質特征，符合學生的認知規律，能讓學生體會到函數來源于生活，又服務于生活。