Mathematica在高等數學中的簡單應用

陳靜

【摘要】討論了利用Mathematica軟件畫圖求極限以及單調性等，并用此軟件進行計算.

【關鍵詞】Mathematica;高等數學;畫圖;計算

高等數學是高等教育階段一門重要的基礎課，但由于其知識點多，邏輯性強，計算量大，抽象性高，不少同學覺得高等數學空洞、枯燥、乏味.為了增強同學們學習高等數學的興趣，平時教學過程中結合現代信息技術教學，已成為一個必然趨勢.而Mathematica軟件使用簡單，功能強大，借助它可以使課程更加形象化、生動化.

一、借助Mathematica軟件畫圖解決問題

1.在極限中的應用

利用極限的定義來求極限的關鍵是先要畫出函數的圖像，對于畫一些稍微復雜的函數的圖像，我們就可以借助Mathematica軟件來解決.

例1 求limx→0e1x.

解 Plot[Exp[1/x]，{x，-2，1}]

圖 1

由此圖觀察，發現當x從0的左側趨向于0時，函數值無限接近于0，當x從0的右側趨向于0時，函數值無限增大，所以此函數在0處的極限不存在.

例2 利用極限的定義，通過畫圖來驗證兩個重要極限.

解 Plot[sin[x]/x，{x，-1，1}]

圖 2

由此圖可以看出，與第一個重要極限limx→0sinxx=1結論符合.

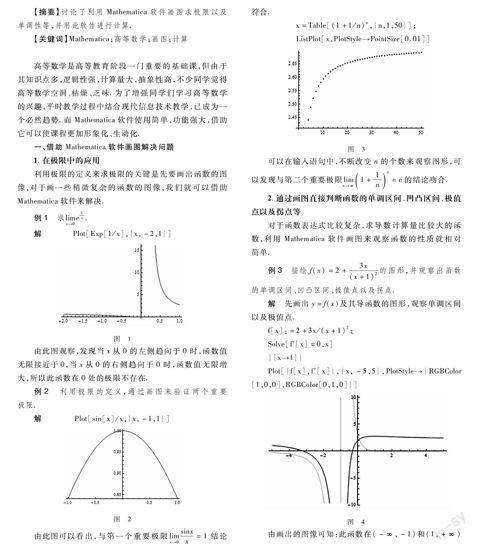
x=Table[（1+1/n）n，{n，1，50}];

ListPlot[x，PlotStyle→PointSize[0.01]]

圖 3

可以在輸入語句中，不斷改變n的個數來觀察圖形，可以發現與第二個重要極限limn→∞1+1nn=e的結論吻合.

2.通過畫圖直接判斷函數的單調區間、凹凸區間、極值點以及拐點等

對于函數表達式比較復雜，求導數計算量比較大的函數，利用Mathematica軟件畫圖來觀察函數的性質就相對簡單.

例3 描繪f（x）=2+3x（x+1）2的圖形，并觀察出函數的單調區間、凹凸區間、極值點以及拐點.

解 先畫出y=f（x）及其導函數的圖形，觀察單調區間以及極值點.

f[x]：=2+3x/（x+1）2;

Solve[f′[x]=0，x]

{{x→1}}

Plot[{f[x]，f′[x]}，{x，-5，5}，PlotStyle→{RGBColor[1，0，0]，RGBColor[0，1，0]}]

圖 4

由畫出的圖像可知：此函數在（-∞，-1）和（1，+∞）上單調遞減，在（-1，1）上單調遞增;x=1為極大值點.

再畫出y=f（x）及其二階導函數的圖形，觀察其凹凸區間和拐點.

f[x_]：=2+3x（x+1）^2;

g[x_]=D[f[x]，{x，2}]

18x（1+x）4-12（1+x）3

Slove[g[x]=0，x]

{{x→2}}

Plot[{f[x]，g[x]}，{x，-5，5}，PlotStyle→{RGBColor[1，0，0]，RGBColor[0，0，1]}]

圖 5

此函數在（-∞，-1）和（-1，2）上是凸的，在（2，+∞）上是凹的;拐點是x=2.

二、利用Mathematica軟件計算，提高解題速度

1.求極限

Limit[f[x]，x->x0];

Limit[f[x]，x->x0，Direction->-1];Limit[f[x]，x->x0，Direction->1].

上述三個命令分別表示求函數在x0處的極限、左極限和右極限.

例4 求limx→∞sinxx2-π2.

解 ln[3]：=Limitsin[x]x2-π2，x→π

Out[3]=-12π

2.求導數

D[f[x]，x]——求函數的導數;D[f[x]，{x，n}]——求函數的n階導數.

例5 求y=（1+cosx）1x的導數.

解 ln[4]：=D[（1+cos[x]）1x，x]

Out[4]=（1+cos[x]）1x-log[1-cos[x]]x2-sin[x]x（1+cos[x]）

3.求極小值

FindMinimum[f[x]，{x，x0}]——求函數在點x0附近的極小值.

例6 求函數f（x）=x3（6x+7）2的極小值.

解 ln[6]：=FindMinimum[x3（6x+7）2，{x，-1}]

Out[6]={-1.3906，{x→-0.7}}

即：在x=-0.7處取得極小值-1.3906.

4.求積分

Integrate[f[x]，x]——計算不定積分∫f（x）dx;

Integrate[f[x]，{x，a，b}]——計算定積分∫baf（x）dx.

例7 求解不定積分∫sin（lnx）dx.

解 ln[1]：=Integrate[sin[log[x]]，x]

Out[1]=-12xcos[log[x]]-12xsin[log[x]]

5.求微分方程

DSolve[方程，y，x]——求以x為自變量的方程的解;

DSolve[{方程1，方程2，…}，y，{x，xmin，xmax}]——求函數y的數值解，x屬于[xmin，xmax];

DSolve[{方程1，方程2，…}，{y1，y2，…}，{x，xmin，xmax}]——求多個函數yi的數值解.

例8 求微分方程y″-2y′+5y=exsin2x的通解.

解 ln[1]：=DSolve[y″[x]-2y′[x]+5y[x]==ex*sin[x]，y[x]，x]

Out[1]={{y[x]-exC[2]cos[2x]+exC[1]sin[2x]-112ex（4cos[2x]sin[x]3-3cos[x]sin[2x]+cos[3x]sin[2x]）}}

Mathematica軟件具有強大的計算功能，便捷的使用方法，在高等數學中使用廣泛，具有很強的應用性.在高等數學的教學中穿插Mathematica軟件的學習，可以提高學生的學習興趣，培養學生會用數學知識，借助計算機，提高分析和計算應用問題的能力.

【參考文獻】

[1]汪曉虹.高等數學實驗——學軟件 做數學[M].北京：國防工業出版社，2010.

[2]蔡俊娟.Mathematica在高等數學教學中的應用[J].長江大學學報（自然科學版），2009（4）：346-348.

[3]紀宏偉，蘇瑩，高金新.Mathematica在高等數學中的典型問題應用探索[J].貴州師院學院學報，2011（3）：20-23.

[4]曹瑞成，姜海勤.高等數學[M].北京：化學工業出版社，2007.