二次函數(shù)在平面幾何的應(yīng)用

翁怡玲

【摘要】 平面幾何圖形是初中的一大重點，而二次函數(shù)也是初中的重點知識之一，然而把這兩者結(jié)合在一起，就變成了大難點. 初中的平面幾何主要涉及到直線、三角形、四邊形和圓，本文也將對前面三種類型來談?wù)劧魏瘮?shù)在平面幾何的應(yīng)用.

【關(guān)鍵詞】 二次函數(shù)；平面幾何；應(yīng)用

初中平面幾何圖形是高中空間幾何的鋪墊，如果無法掌握初中平面幾何題目的解答方法，將來學(xué)習(xí)高中空間幾何就難上加難. 近年來，中考特愛把二次函數(shù)與平面幾何結(jié)合在一起，因此本文將對二次函數(shù)在平面幾何中的直線、三角形、四邊形的應(yīng)用進(jìn)行分析.

一、二次函數(shù)與直線

二次函數(shù)與直線應(yīng)該是除了二次函數(shù)與點之外第二簡單的了. 但是有時候二次函數(shù)與直線也是可以很復(fù)制的，而且還會涉及到三角形的面積. 根據(jù)筆者的教學(xué)經(jīng)驗，建議教師在講解這部分知識點還是選擇簡單一點的題型進(jìn)行講解，這樣可以照顧到大部分的學(xué)生. 因為在考試中，簡單中等的題型所占的比例還是比復(fù)雜的題型要大.

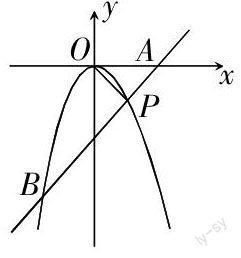
例：如圖，拋物線y = ax2（a ≠ 0）與直線AB交于點P（4，-4），連接OP，則OP = AP，求二次函數(shù)的解析式及拋物線與直線AB另一個交點B的坐標(biāo)

解這道題的關(guān)鍵在于2個坐標(biāo)點，就是點A和點P，尤其是點P是最關(guān)鍵的. 在解題之前，教師應(yīng)當(dāng)引導(dǎo)學(xué)生觀察圖像，找出解題的突破口，這樣才省時，而且方向也是正確的. 通常什么東西同時跟另外兩者都有關(guān)系，這個東西就是解題的關(guān)鍵. 一眼看過去，很明顯，點P既在直線AB上， 同時也在拋物線y = ax2（a ≠ 0）上. 所以要求直線AB的解析式和二次函數(shù)的解析式都必須用到點P的坐標(biāo). 首先要求出直線AB的解析式，現(xiàn)在只知道點P的坐標(biāo)，還要求A、B兩點中其中一個點. 很明顯點A的坐標(biāo)是比較好求出的，由于OP = AP，則點A（8，0）. 再將A、P坐標(biāo)代入直線解析式y(tǒng) = mx + n，求出m，n的值. 再將點P的坐標(biāo)帶入二次函數(shù)中，求出二次函數(shù)的解析式，再和直線AB解析式組成方程組，求出點B的坐標(biāo).

二、二次函數(shù)和三角形

一般，出題者都會考查二次函數(shù)的圖像上是否存在一點使得某三角形存在或者某2個三角形相似，或者考查利用二次函數(shù)求三角形的面積. 相對來說，考查三角形的面積題目占的比例會比較多，而是否存在一個點使得三角形存在通常只在最后一道大題里面進(jìn)行考核. 因此，筆者要分析的是如何利用二次函數(shù)求三角形的面積.

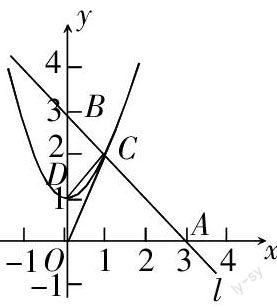
例：如圖，直線l經(jīng)過A（3，0），B（0，3）兩點，且與二次函數(shù)y = x2+1的圖像，在第一象內(nèi)相交于點C，求：

（1）△AOC的面積；

（2）二次函數(shù)圖像的頂點與點A、B組成的三角形的面積

這道題說簡單又不簡單，因為它不單單是求一個三角形的面積，而是兩個三角形的面積. 那面對這樣的題目，我們應(yīng)該如何解決. 方法就是逐一突破. （1）根據(jù)三角形的面積公式，要求△AOC的面積，需求出OA的長度和C點的縱坐標(biāo). 由點A坐標(biāo)，可以得出OA = 3，再利用系數(shù)待定法設(shè)直線AB的解析式為y = kx + b，求出直線AB的解析式，再與二次函數(shù)的解析式聯(lián)立，求出方程組的解，可得C點的縱坐標(biāo)的值. （2）要求二次函數(shù)圖像的頂點與點A、B組成的三角形的面積，就要先求出二次函數(shù)圖像的頂點D的坐標(biāo)，由頂點公式可以求出D的坐標(biāo)（0，1），再根據(jù)三角面積公式即可求出該三角形的面積. 在此處，教師需要提醒學(xué)生，以后遇到點在坐標(biāo)軸上，都可以利用頂點公式求出這些點的坐標(biāo).

三、二次函數(shù)與四邊形

初中所學(xué)的四邊形，包括平行四邊形、梯形、菱形、矩形等. 二次函數(shù)和四邊形的結(jié)合通常考查的也是二次函數(shù)的解析式和四邊形的面積. 通常只要求出四邊形的4個頂點的坐標(biāo)就能求出該圖形的面積. 但是有一種比較特殊的考查方式，就是利用二次函數(shù)求四邊形的面積最大值，這個又涉及到函數(shù)的最值問題，而不單單是幾何面積這么簡單.

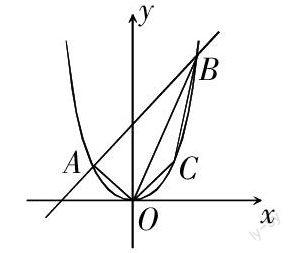
例：如圖，二次函數(shù)y = ax2 + bx的圖像與一次函數(shù)y = x + 2的圖像交于A、B兩點，點A的菁優(yōu)網(wǎng)橫坐標(biāo)是-1，點B的橫坐標(biāo)是2.

（1）求二次函數(shù)的表達(dá)式；

（2）設(shè)點C在二次函數(shù)圖像的OB段上，求四邊形OABC面積的最大值把x = -1和2分別代入y = x + 2，就可以求出A，B的坐標(biāo)分別為（-1，1），（2，4），把這兩點的坐標(biāo)代入二次函數(shù)的解析式，就可以求出二次函數(shù)的解析式y(tǒng) = x2.

由于點C是動點，因此要設(shè)點C的坐標(biāo)為（x，y）. 過點A、B作AM⊥x軸，BN⊥x軸，分別交于M、N.過點C作CP⊥BN于P，這樣四邊形OABC面積就可以用函數(shù)值表示了. 然后分別表示出，梯形AMNB的面積、△AOM的面積、△BCP的面積、四邊形CPNO的面積，則四邊形OABC面積s = 梯形AMNB的面積-△AOM的面積-△BCP的面積-四邊形CPNO的面積 = -x2 + 2x + 3，再求出該二次函數(shù)的最大值即為四邊形OABC面積的最大值. 教師主要引導(dǎo)學(xué)生將面積的最值問題一般要轉(zhuǎn)化為函數(shù)的最值問題，再依據(jù)函數(shù)的性質(zhì)解決.

另外，二次函數(shù)和圓的結(jié)合，也是常考的知識點. 如果考查的是動點的問題，則題目比較復(fù)雜，主要考查學(xué)生的綜合能力，涉及的知識點也是較為廣泛的. 這類的問題需要靠學(xué)生平時的個人積累以及思維能力的培養(yǎng). 通過以上三個例子，可以發(fā)現(xiàn)數(shù)形結(jié)合的思想初中數(shù)學(xué)教與學(xué)可以同時解決函數(shù)問題和幾何問題，也越來越受教師和學(xué)生的青睞. 教師要在平時的課堂中強(qiáng)化數(shù)形結(jié)合的思想觀念，這樣幫助學(xué)生突破函數(shù)難關(guān)，走出困境，更加熱愛數(shù)學(xué).

【參考文獻(xiàn)】

[1]陸文娟.二次函數(shù)圖像中三角形面積計算問題.初中數(shù)學(xué)教與學(xué)，2012（19）：15.

[2]劉洪生.二次函數(shù)解簡單動態(tài)幾何中的面積最值問題. 新課程（下），2013（04）：135.

[3]幸利.利用數(shù)形結(jié)合 突破函數(shù)難關(guān).初中數(shù)學(xué)教與學(xué)，2014（08）：14-16.

[4]王競進(jìn).二次函數(shù)與幾何圖形綜合題例析.初中生世界，2015（23）：39-43.