乘法分配律的教學實踐與思考

鄭德華

【摘要】 乘法分配律的學習是個難點，可以從孕伏中滲透、意義中建構、練習中達成、拓展中提升加以有效突破.

【關鍵詞】 乘法分配律；滲透；意義；練習；拓展

小學階段學習了加法交換律、結合律，乘法交換律、結合律，乘法分配律，簡稱“五律”，是以例題的形式呈現學習的；而“兩性質”即減法性質與除法性質是結合在練習中滲透的. 這“五律”“兩性質”是學生進行簡便運算的依據. 縱觀多年來的教學實踐，學生對于乘法分配律的學習始終是個難點，好些學生總是跨不過這道門檻. 因此筆者多年來一直在探究思考，如何讓學生能自主地跨過學習乘法分配律這道門檻，讓學習真正地發生. 我反復嘗試著、反思著，摸索出了比較可行的方法，現撰寫成文，以期能起到拋磚引玉的效果.

一、孕伏中滲透

乘法分配律的學習是個難點，突破難點的方法之一，就是做好前期孕伏滲透，以便分散難點. 可以從以下方面進行滲透.

1. 學習兩位數乘一位數時孕伏滲透

比如，學習12 × 3，結合情境圖、列豎式計算，讓學生理解把12分成10 + 2的和，先算2個3的積，再算10個3的積，最后把兩積合起來. 關鍵再引導一步讓學生把算式表示出來，得出算式是：12 × 3 = （2 + 10） × 3 = 2 × 3 + 10 × 3.讓學生對著算式讀幾遍，12 × 3等于2加10的和乘3等于2個3的積加上10個3的積，凸顯這一環節，目的就是有意識地滲透乘法分配律的結構.

2. 學習混合運算時孕伏滲透

蘇教版四年級上冊學習乘加、乘減混合運算時，練習中已經安排形如這樣的題組：

36 × 25 + 36 × 75，36 × （25 + 75）.

這里安排這樣的題組練習，目的有二：其一是鞏固混合運算的運算順序，提高運算技能；其二就是編者有意識地孕伏滲透乘法分配律的知識，讓學生通過練習，對比感知這樣的兩個算式是有聯系的，是可以用等號連接起來的了解了編者的良苦用心，那么應該如何滲透呢？筆者是這樣教學的：在學生觀察這兩個算式的基礎上，先讓學生猜想這兩個算式的結果怎樣，有的學生說相等. 接著讓學生通過計算加以驗證，原來兩個算式的結果的確相等，用等號把兩個算式連起來，齊讀一遍. 最后引導學生通過乘法的意義加以解釋為什么兩道題的結果相等. 因為左邊的算式表示25個36加上75個36，也就是（25 + 75）個36，即100個36，而右邊的算式也表示100個36，所以兩道算式的結果是相等的. 那么在計算這兩道時，哪道算起來更方便呢？今后我們在計算36 × 25 + 36 × 75時第一步可以怎樣改寫呢？這就是下學期我們要學習的運算律.

3. 學習長方形的周長時孕伏滲透

學生在建構長方形的周長公式時，會出現長 × 2 + 寬 × 2，也會出現（長 + 寬） × 2. 這時教師就可以引導學生把（長 + 寬） × 2寫成長 × 2 + 寬 × 2，讓學生明白兩者之間的聯系. 為滲透乘法分配律的知識做好鋪墊.

如果我們的老師能在這些知識的建構處有意識地引導、滲透，學生的前期學習中就具備有乘法分配律的影子，到真正學習乘法分配律時就不會感到陌生，有種似曾相識的感覺，學生接納起來就容易得多了.

二、意義中建構

乘法分配律難就難在學生對乘法算式意義的不理解，學生中常出現這樣的錯誤就足以說明這一點. 比如（30 + 2） × 16，有的學生是這樣計算的：（30 + 2） × 16 = 30 × 16 + 2，只把30乘16，而2不乘16，說明學生對算式表示的意義不理解. 因此新知的教學要從乘法的意義入手，讓學生從意義的角度來建構乘法分配律.

從例題中學生得出（6 + 4） × 24 = 6 × 24 + 4 × 24，讓學生從意義的角度解釋兩個算式相等的理由，左邊算式表示（6 + 4）的和個24，即10個24，右邊的算式表示6個24加上4個24，也是10個24. 在學生提出“兩個數的和乘一個數等于兩個數分別乘這個數再求和”的猜想，學生舉例驗證這一猜想時，也讓學生從乘法意義的角度來解釋，觀察眾多例子歸納出乘法分配律的字母表達式（a + b） × c = a × c + b × c，仍讓學生用乘法的意義加以解釋，（a + b）的和個c可以寫成a個c加上b個c；反過來a個c加上b個c可以寫成（a + b）的和個c. 從初步發現（6 + 4） × 24 = 6 × 24 + 4 × 24，到學生提出猜想、舉例驗證、歸納規律，始終以乘法的意義為抓手，觸及問題的實質，有效地避免了有的學生依葫蘆畫瓢，機械記憶， 只知其一不知其二.

三、練習中達成

練習是學生鞏固新知、形成技能、發展思維的有力載體. 針對乘法分配律的特點、學生的易錯點，筆者以教科書的練一練和練習十的練習為載體設計了四個層次的練習.

（一）基本練習

1. 在□里填數，在○里填上運算符號.

本題練習主要是讓學生鞏固乘法分配律的結構，從正用到反用，又從反用到正用，在這個正、反用的有效對接中，掌握乘法分配律的結構. 施教時，先讓學生獨立完成，再選擇一道正用和一道反用的等式讓學生用乘法的意義解釋填寫的理由.

2. 橫著看，在得數相同的算式后畫“？菁”.

本題較上一題有所變化，尤其是第三、第四兩組題，第三組題出現了1個74，第四組題得數不相同，從反例讓學生感受乘法分配律的結構. 教學時，先讓學生獨立完成，再讓學生用乘法的意義解釋 74 × （20 + 1） = 74 × 20 + 74 的理由，40 × 50 + 50 × 90不等于40 × （50 + 90）的理由，從中又讓學生分別寫出40 × 50 + 50 × 90和40 × （50 + 90）的另一半.

（二）對比練習

算一算，比一比，每組中哪一題的計算比較簡便？

第一組：64 × 8 + 36 × 8 （64 + 36） × 8

第二組：25 × 17 + 25 × 3 25 × （17 + 3）

本題練習主要目的是讓學生感受運用乘法分配律能使某些計算簡便. 施教時，筆者先出示第一組，讓學生觀察兩道算式，猜想它們的結果是否相等. 之后，通過計算、用乘法的意義解釋驗證. 從而得出64 × 8 + 36 × 8寫成（64 + 36） × 8 計算較簡便. 獨立完成第二組，感受乘法分配律的價值.

（三）解釋練習

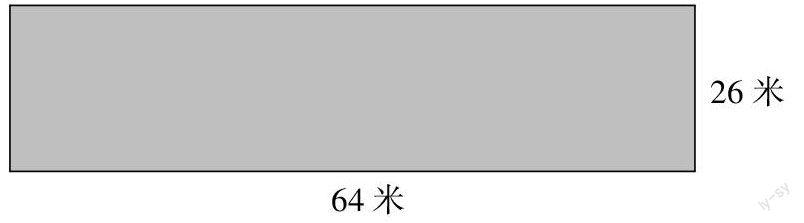
用兩種不同的方法計算長方形菜地（如下圖）的周長，并說說它們之間的聯系.

本題練習主要宗旨是讓學生回顧前面已學的長方形周長的計算方法：（長 + 寬） × 2 = 長 × 2 + 寬 × 2，它們之間的聯系紐帶正是運用了乘法分配律，讓學生感受乘法分配律在以往的學習中已經用過，只不過是當時沒有明晰罷了.

四、拓展中提升

乘法分配律之所以難，還在于它的多變. 有的要先拆數，如102 × 36要把102拆成100 + 2的和；有的是從兩積之和延伸到兩積之差，如25 × 176 - 25 × 76；有的還要制造共同乘數，如330 × 42 + 580 × 33，原式中沒有共同乘數，但根據等積變形的原理可以將原式變為330 × 42 + 58 × 330或33 × 420 + 580 × 33. 因此，為了盤活學生對乘法分配律的真正運用，筆者進行了拓展練習，在練習中提升學生對乘法分配律本質的認識，培養學生透過現象看本質的能力.

總之，對于乘法分配律的教學，要抓住知識的源頭，做好孕伏中的滲透；要以乘法的意義為抓手，運用意義的解釋建構新知；要以練習為主線，在練習中達成，拓展中提升.