意料之外，情理之中
——勾股定理之外的智慧“生成”

☉南京師范大學附屬中學樹人學校 王玉琴

意料之外，情理之中
——勾股定理之外的智慧“生成”

☉南京師范大學附屬中學樹人學校 王玉琴

每個學生都是鮮活靈動的智慧生命個體，并非是按照預設程序機械運動的機器，因而隨機生成的“意外”是課堂上常見的現象.有些意外的生成能夠帶來豐碩的成果，教師如果善用教學智慧，實現師生、生生之間智慧的碰撞，那么很多課堂將演化成師生的一段智慧生命的精神之旅.正如蘇霍姆林斯基說：“教育的技巧并不在于能預見到課堂的細枝末節，而在于根據當時的具體情況，巧妙地在學生不知不覺中做出相應的變動.”但意料之外的智慧生成，也并非完全出于偶然，正如靈感的出現，也是基于學習或研究者一定的知識基礎和對問題的深入思索，而且，由于教學時間的限制，我們不可能對所有課都任由學生自由探索，一個智慧課堂，應更多地探討適合學生知識、能力基礎和學習方式、心理特點的有價值的問題.這就需要我們對一些典型的智慧生成教學案例，做必要的反思、探究，以便在有限的教學時空內，更多地激發學生潛在的智慧和求知熱情.

一、課堂簡錄

筆者平時上兩個班的課，在進行勾股定理新授課教學時，其中一個班的課上出現了一個意外提問.

生1：老師，那么非直角三角形的三邊的平方具有什么關系？

當時筆者聽了之后再想是繼續本節課的教學內容還是解決該生的問題？在筆者任教的兩個班中，這個班的同學基礎好、能力強，平時就有許多同學喜歡鉆研數學問題，也常有不少小發現，而且這位同學提出的問題是剛學的勾股定理的自然拓展，也是思維觸角的自然延伸，從方法、思維上均有貫通之處，既有進一步研究的基礎和價值，又比較適合這個班的學情，相信他們中多數人有能力探究這個問題，這對鼓勵他們的探究熱情、激活他們的思維、鞏固所學的知識均有益處，顯然比課后做幾道勾股定理的應用題更有意義.瞬間猶豫后，筆者決定把時間讓給學生，讓他們在操作、思考中，展現、張揚個體生命中的智慧.如果一個個鮮活靈動而富有個性的智慧生命被完全禁錮在教師事先給定的框架中，這既是教育的悲哀，也是對智慧的漠視.

師：這個問題問得非常好！請同學們分學習小組討論，看哪個小組能幫助他解決這個問題.

這下課堂炸開了鍋，討論氛圍之熱烈超乎筆者的想象，立刻便有人躍躍欲試.

生2：老師，∠C還是最大角嗎？

師：好，為了表達方便，我們不妨規定鈍角△ABC中，a≤b≤c.

生3：構造以a、b為直角邊的直角三角形，如圖1，過頂點C作CD⊥AC，同時取CD=CB=a（這里不夠嚴謹，但容易說明點D在△ABC外——筆者注），在Rt△ACD中，a2+ b2=AD2，而∠ADB＞∠CDB=∠CBD＞∠ABD，所以AB＞AD，即a2+b2＜AB2=c2.（證法1）

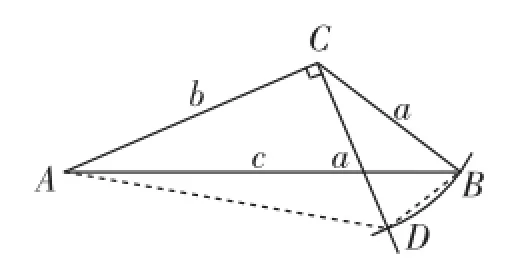
圖1

圖2

生3剛說完，生4迫不及待地舉起了手.

生4：老師，c＞AD還可這樣說理：如圖2，作∠DCB的平分線CE，交AB于點E，連接ED，可得△DCE≌△BCE，于是有ED=EB，而AE+ED＞AD，所以c＞AD.（證法2）

師：很棒！上面的證法構造了以a、b為直角邊的直角三角形，運用勾股定理得到直角三角形的三邊平方關系，然后再將這個直角三角形的斜邊AD與鈍角三角形的最長邊c做比較，最終得出結論.還可以構造怎樣的直角三角形呢？

生5：還可構造以c為斜邊的直角三角形，如圖3（嚴格說來，易證點E在△ABC外），由于∠ACE與∠BCE均為鈍角，即為三角形中的最大角，所以有AE＞AC，BE＞BC，而AE2+BE2=AB2，所以a2+b2＜AB2=c2.（證法3）

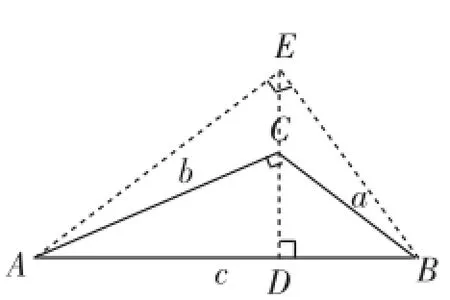
圖3

師：簡潔明了，非常漂亮！可見，欲求鈍角三角形的三邊平方關系，可將鈍角三角形問題轉化為與它相關的直角三角形問題.至于怎樣轉化，怎樣構造直角三角形，方法可以是多種多樣的，大家再試試.

生6：也可以過點B作高線，如圖4，過點B作BE⊥AC交AC的延長線于點E，由勾股定理有x2+y2=a2，（x+b）2+y2= c2，將兩式相減得c2-a2=2xb+ b2，所以a2+b2＜c2.（證法4）

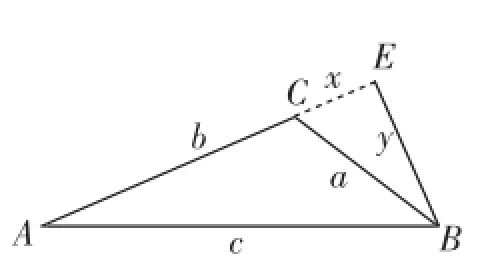
圖4

師：好！通過作高BE，化斜為直，構造了兩個直角三角形：△BEC，△BEA.以上幾種證法的思路，都是構造直角三角形進行轉化，借助于勾股定理的結論解決問題.想一想，從勾股定理的學習過程中我們還能得到什么啟發，還可以找到其他的證明思路嗎？

生7：老師，老師，還可以用圖形的面積來解決！

師：太好了！這是證明勾股定理的主要方法，學習一個定理，我們不僅要知道它的結論和應用，還要理解證明的過程和方法，并學會將方法用于解決其他問題.生7，請把你的面積方法說給大家聽聽.

生7：將△ABC繞著點C逆時針旋轉90°得到△A′B′C，如圖5，連接AA′、A′B、BB′、B′A，因為四邊形AA′BB′的面積為AB· A′B′=c2，同時它又等于△BCB′、△ACA′、△BCA′、△ACB′的面積和，所以所以（.證法5）

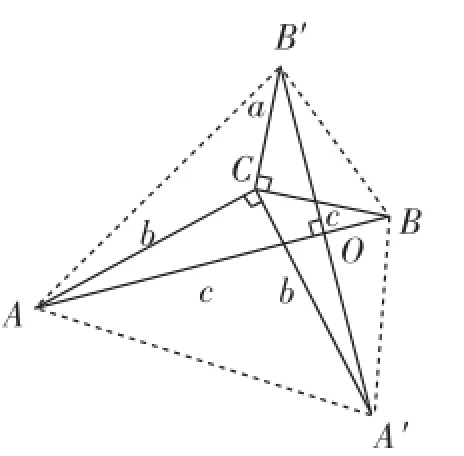
圖5

學生7發現如此精巧的證明方法，贏得了大家的喝彩.這時課堂研討氣氛之熱烈，學生思維之活躍，興趣之濃厚，讓筆者感慨萬分.此法一經說出似乎平易，實為天資聰明的學生靈機一動閃出的智慧火花，多數學生不易想到.

此時，同學們和筆者的臉上都洋溢著收獲的喜悅，下課的鈴聲在不知不覺中已悄然響起，可同學們還意猶未盡.掌聲也在不經意中再次驟然響起，這或許是同學們此時心態的最好呈現.

圖6

二、感悟與反思

這堂課大大超出了筆者的預設，但這樣的意外卻帶來了精彩的智慧生成，不能不反思，自己在課堂上幸運地占有了如此豐富的教學資源（優秀的學生群體，學生的思維、創新方法的多樣性，還包括學生自然生成的有價值的提問等），卻差點扼殺了學生的思維，錯過使學生享受探求知識過程的樂趣和摘到智慧果實的良機.因此，有必要以此為契機，深入探討數學課堂智慧生成的特征和條件.

成尚榮教授曾指出：“智慧是一種整體品質，它在情境中誕生和表現，以美德和創造為方向，以能力為核心，以敏感和頓悟為特征，以機智為主要表現形式，科學素養與人文素養的結合賦予它底蘊和張力.”

數學課堂的智慧生成，是在數學思維的激發態、數學思想火花的靈光乍現中孕育迸發的.

反思這節課上學生的精彩生成，可以發現處于思維激發態的智慧具有以下一些特征，從中也許我們可以悟出一些數學教學的“真經”.

（一）智慧生成的特征

1.借力借法，變形變通

智者不以一己之力蠻干，而善于借助已有成果、方法，或借助于他人的思維、力量進行碰撞、交流；若問題不具備條件，則善于改造、變通，將其轉化為已經解決的問題.這種轉化化歸的思想，在數學解題中屢見不鮮.例如證法1～4，將鈍角三角形中邊的平方關系問題通過構造、分解圖形的方法，轉化為直角三角形問題，從而運用勾股定理獲證.

2.思維靈動，動靜相生

思維靈動而充滿創造性，是智慧課堂的重要特征.幾何學研究運動變化中的不變性，新課程幾何引入旋轉、平移、對稱、相似等變換，借助它們進行線段、角、區域的恒等、放縮轉換，使圖形成為動態的，在分分合合、運動變化中我們抓住不變性（量），給創造帶來更多的空間和靈性.本課的多種證法中，不乏對稱、等積變換的身影.

3.大膽想象，不離本質

證法1中，可以把角C想象成一把開合自如的剪刀，著張角C的減小，剪刀開口兩個尖端的距離也在縮小.股定理的面積法證明，其本質是構造圖形，使其面積含有與三邊a，b，c平方有關的量，其中多數證法是構造正方形、直角三角形、梯形等規則圖形.證法5卻大膽想象，構造了一個不規則四邊形.

4.整體感悟，直覺把握

智慧往往表現為對事物的宏觀的把握，或一種穿越細節和邏輯鏈條的直覺、頓悟，如證法3，學生可以從整體上感悟到當角C為鈍角時，所對的邊c相對于a、b比角C為直角時要大些，因而直覺上感到可與角C為直角時相應的勾股定理的結論聯系起來.當學生7興奮地說：“老師，老師，還可以用圖形的面積來解決！”這時他很可能是由于頓悟而驚喜.

5.整合遷移，融會貫通

智慧常生成于知識交匯處，這里是思想碰撞、知識聯系的沃土，也是創造的源泉之一.如證法5，將面積法和變換法結合起來，顯得新穎別致.智慧也常生成于知識、方法的遷移、類比，如魯班從葉子的銳利類比聯想，發明了鋸子.證法6正是從勾股定理的歐幾里得證法，加以巧妙遷移而得.

（二）智慧生成的條件

本節課上，學生的智慧火花迸發，處于思如涌泉的激發態，我們不妨冷靜地進行理性反思：為何這個問題能產生如此豐富的結果？除了學生的良好素質、教師的熱情鼓勵與適時點撥、平時探究能力和創新意識的培養以外，問題的提出、知識的儲備、方法的掌握、能力的培養等，也為智慧的生成打下了基礎.細思之，本課的智慧生成，既是意料之外，也在情理之中.

綜上所述，把握智慧課堂的特點，了解智慧孕育的條件，可以更好地抓住課堂上稍縱即逝的意外契機，及時促進智慧的生成，有意識地營造智慧的課堂.

1.馬夫.初中數學教學策略［M］.北京：北京師范大學出版社，2010.

2.黃建平.通過巧設橋梁來提升學生的數學說題能力［J］.中學數學（下），2014（9）.W