一道題，三節課
——筆者的習題教學課

☉湖北省武漢市第三寄宿中學 何亞琴

一道題，三節課
——筆者的習題教學課

☉湖北省武漢市第三寄宿中學 何亞琴

數學新課標在原來的培養學生分析和解決問題能力的基礎上，進一步提出培養學生發現和提出問題的能力.我們數學教師如何將這種理念貫穿到我們平常的數學教學中，是我們數學教師應該深入思考和反思的.

近段時間筆者有意在培養學生發現問題的能力上做了一些有意義的嘗試，效果不錯！這里筆者將一道幾何題的教學推進過程呈現如下.

一、第一節課

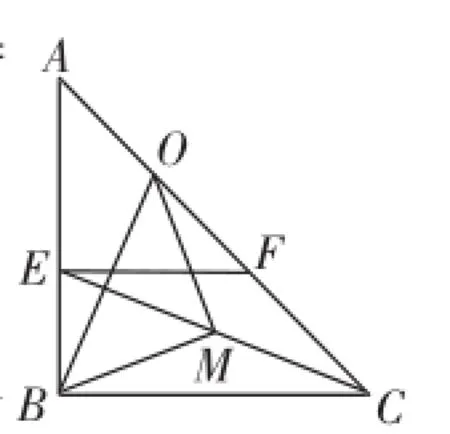
圖1

圖2

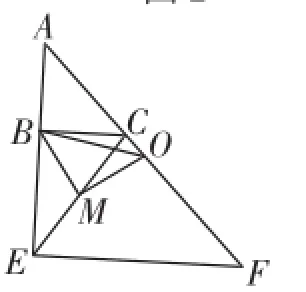
圖3

例題如圖1，在△ABC中，∠ABC＝90°，AB=BC.點E、F分別在邊AB、AC上，且AE=EF，點O、M分別為AF、CE的中點，判斷△MOB的形狀.

本題是在學習了直角三角形斜邊上的中線等于斜邊的一半后配套的練

習題，當然解法也非常簡單，連接EO，在Rt△OEC和Rt△BEC中，直接運用定理不難得出OM=BM，且∠BMO=90°，從而得到△BMO為等腰直角三角形.

如果我們在教學過程中僅僅滿足于學生會解題，以及怎么讓學生更快地了解一道題的解法，并不能達到我們新課標提出的培養學生發現問題的能力，在教學過程中我們可以從最簡單的圖形變換開始入手.

在教學完以上習題后筆者對條件做了如下修改，把“點E、F分別在邊AB、AC上”改成了“點E、F分別在直線AB、AC上”，再追問學生，上述結論還成立嗎？

這個時候學生開始討論起來，有的學生說“可以”，有的學生說“不成立”，還有一部分學生在埋頭畫圖.很快有同學畫出圖2所示的圖形.

有學生說：“還有如圖3所示的圖形.”

這時有學生提出：“這兩個圖形只說明了一種情況，E、F兩點都在線段AB、AC的延長線上，是否會出現一個點在線段上另一個點在線段的延長線上呢？”

筆者及時肯定學生能夠提出這樣的問題，讓學生自己再畫圖說明此種情況是否成立？

當然很明顯是不成立的！以上兩種情況證明方法類似于例題的圖形的證明.有了以上變換的經驗，有學生大膽提出了以下的問題：“其實這里可以去掉‘點E、F分別在邊AB、AC上，且AE=EF’和‘點O為AF的中點’這兩個條件.”這樣的提問讓很多學生馬上反駁起來：“這是不可能的！”此時提問的同學鎮定地說：“只要△AOE為等腰直角三角形就可以！”于是這個學生很快在黑板上畫出了圖形，如圖4.

通過畫出這個圖形，反駁的同學馬上心服口服，這個時候筆者極力肯定這位同學的豐富的想象力和嚴密的邏輯思維能力，以及看問題能看出其中的本質內容.

此時班上的研討氣氛已經非常濃郁了，又有學生提出了更新的見解，他非常肯定地說：“老師！我發現了一個很重要的結論！”其他學生用期待的眼神望著他，他繼續說：“這里只要是兩個等腰直角三角形共一個銳角頂點，另一個銳角頂點的連線的中點和兩個三角形的直角頂點相連所得到的三角形都是等腰直角三角形！”于是他急急忙忙地跑上講臺在黑板上畫出如圖5~圖7所示的圖形.

圖4

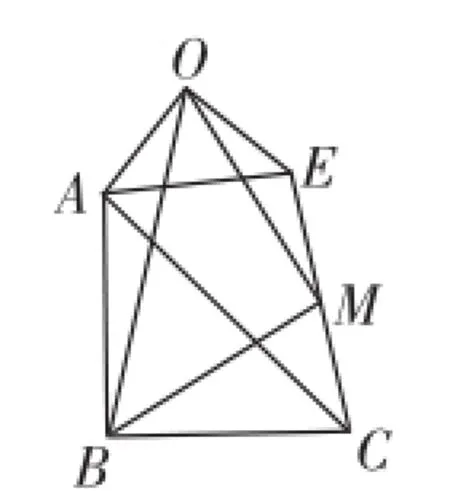
圖5

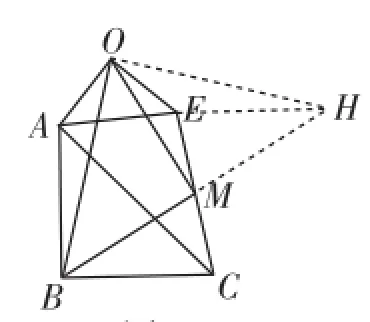
圖6

圖7

如果真是這樣，這個結論怎么證明呢？筆者即時地啟發學生，很快就有學生用下面兩種方法進行了證明.

解法一：（中線倍長法）延長BM到H使MH=BM，連接OH，EH，由△BMC≌△HME得到EH=BC且EH∥BC.而BC=BA，所以EH=BA.已知EO=OA，有∠HEO=360°-∠CEH-∠CEA-45°=315°-∠CEH-∠CEA.而五邊形BCEOA中，∠BAO=540°-∠BCE-（∠CEA+45°）-90°-90°＝315°-∠CEH-∠CEA，即∠HEO=∠BAO，也就是在此處構造了等腰Rt△AOE和等腰Rt△BOH，所以可以得到△BAO≌△HEO，則OB=OH，∠BOA=∠EOA，M為BH的中點，所以△BMO為等腰直角三角形.

解法二：（中位線和斜邊上中線法）分別取AC和AE邊上的中點為G和H，連接MG，BG，MH，OH，根據中位線定理和直角三角形斜邊上的中線等于斜邊的一半可知，MG=OH，BG=MH，其中∠MGB=∠MGC+90°，∠MHO=∠MHE+90°.因為∠MGC=∠GMH=∠MHE，所以∠MGB=∠MHO，因此△MGB≌△MHO.

由∠BMO=∠BMG+∠GMH+∠HMO=∠MOH+∠MHE+∠HMO=90°，得到MB=MO，MB⊥MO，所以△BMO為等腰直角三角形.

這兩種方法對于上述結論的所有變換后的圖形都可證明，但在解法一中證明∠HEO=∠BAO相等時有些微小的變化.筆者在學生證明之后適當地配合著多媒體，利用幾何畫板軟件，很精彩地演示了在其中一個三角形旋轉時，基本圖形變換出來的各種神奇的圖形，讓學生大開眼界.學生驚嘆數學的奇妙，解法的精妙！學生不僅嘗試了解決問題的快樂，還能品嘗到由大膽創新所帶來的感動，這樣的教學使我們的數學教學站到了戰略性的制高點上！

一節課上到這個時候似乎已經非常圓滿了，學生對“兩個等腰直角三角形共一個銳角頂點，另一個銳角頂點的連線的中點和兩個三角形的直角頂點相連所得到的三角形都是等腰直角三角形”深信不疑了，而且還對圖形進行了變換，其實這個結論還有一個很重要的漏洞，學生沒有發現，筆者繼續引導學生發現.這個時候筆者用幾何畫板畫了如圖8所示的圖形.

在這個圖形里很明顯△BMO不是等腰直角三角形，隨著△ABC或者△AEO位置的變換，△BMO的形狀更是跟著變化.問題出在哪里呢？當筆者把這個圖形演示給學生看時，教室里頓時炸開了鍋.這時下課鈴響.筆者故作神秘地跟學生告別，留下了懸疑！

課間操剛結束，就有學生興致勃勃地跑到筆者的辦公室，告訴筆者，他發現了其中的奧秘！并且他手里拿著一大一小兩個等腰直角三角板告訴筆者原因！秘密出在兩個等腰直角三角形的擺放方式不同.當AO、AB重合為一條直線時，兩個三角形的直角如果處在這條直線的兩邊，則上述結論成立，否則不成立！學生還用手中的三角板進行了比劃！

“這真是一個神奇的發現！”筆者由衷地贊嘆！并鼓勵他繼續探索，看還有沒有別的重大發現！

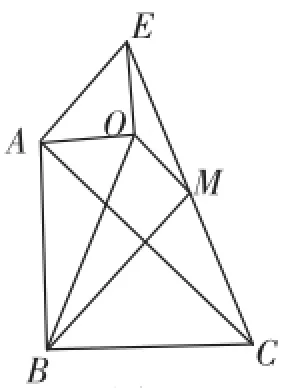
圖8

二、第二節課

第二天筆者繼續帶著電腦進了教室，用幾何畫板作了兩種不同位置擺放的兩個等腰直角三角形，如圖9、圖10所示.

圖9

圖10

其實筆者在這里即時給學生埋下了一個伏筆：等到九年級時我們將研究此時結論不成立的那個圖形！它將會有自己獨特的結論.

教學到這一步，似乎已經功德圓滿了吧.筆者話鋒一轉，提問：“能否把這里的兩個等腰直角三角形換成一般的直角三角形呢？如果換成一般的直角三角形，這兩個直角三角形之間必須有什么樣的聯系呢？”

小組開始了熱烈的討論.

當小組上來展示討論成果時，讓自己對學生的能力刮目相看！

下面是學生代表在黑板上畫出的圖形，如圖11，他們小組討論的結果是：只要∠BAC=∠EAO=α，此時也要注意到兩個三角形擺放的方向性.這時△MBO是等腰三角形，BM= MO，∠BMO=180°-2α，只有當α=45°時∠BMO=90°，也就是等腰直角三角形的情形.

另一個小組特別說明了為什么在這個圖形中不能用解法二來解答的原因.

還有一個小組展示了他們不同的圖形，在證明∠BGM=∠MHO時采用不同的證明方法，這節課學生的學習激情很高，爭先恐后地要求上來講解他們小組的討論結果，課堂氣氛異常活躍！

三、第三節課

圖11

有了前面兩節課的學習，學生對這個圖形已經有了初步的了解，還不能做到隨時隨地從復雜圖形中分辨出來，所以這節課筆者安排了“練就火眼金睛”這個環節.根據幾何畫板的功能筆者將這一基本圖形做了很多的變化，然后不加任何說明，打印了6個不同狀態下的圖形，并復印了人手一份，這里只有8個不同狀態下的圖形，條件結論都沒有，筆者將學生分成6個小組，每組一個圖形開始討論，給這個圖形什么樣的已知條件，得出什么結論！現在將幾個小組編寫的比較經典的習題在這里展示一下，希望能起一個拋磚引玉的作用！

就圖12學生自編了以下幾個不同的習題：

1.在△AEC中，∠A=45°，ED、BC分別為AC、AE邊上的高.

（1）當F為CE邊上的中點時，請判斷△DBF的形狀.

（2）當△DBF為等腰直角三角形時，F是否為EC的中點？

2.D為等腰Rt△ABC的斜邊AC上一點，連接BD，過B點作∠DBF=45°，E為AB延長線上一點，且DE=AD，連接DF，請判斷△DBF的形狀.

3.ED、CB分別為△AEC中AC、AE邊上的高，F是否為EC的中點，連接DF，BF，且△DBF為等腰直角三角形，求∠A的大小.

圖12

圖13

針對圖13學生自編了以下幾道不同的習題：

1.D為等腰Rt△ABC的邊AB上的一點，過D點作DE⊥AB，并截取DE=AD，連接CE，∠ABC的平分線交CE于點F.

（1）求證：F為CE的中點.（2）當D點在AB上移動時，∠FDB的度數是否發生變化？

2.直線AC：y=x+4與x軸交于點A，與y軸交于點C，過點A作AH⊥AC，在AH上任取一點E，連接CE，取CE的中點F，當E點在AH上運動時，∠FBC的度數是否發生變化？若不變，求出角的度數；若變化，求出變化的范圍.

有了以上三節課的教學，讀者試想一下，學生對此類問題還能不認識嗎？而且整個過程中體現了學生獨立的動手能力，培養了學生發現和提出問題的能力，從簡單問題入手，層層推進，推動學生的思維能力，大力加強了學生的數學素養！這樣的習題課學生瘋狂地摯愛著，正是這樣的數學教育，帶來了良好的教學效果！W