洞悉初中數學考題創設的“玄機”

☉江蘇省泰州市孔橋初級中學 田伯青

洞悉初中數學考題創設的“玄機”

☉江蘇省泰州市孔橋初級中學 田伯青

考試是當前檢查學生學習情況和反饋教師教學效果的重要手段之一，試卷中考題的質量顯得十分的重要；新課改要求考題應該在考試大綱的范圍內源自于課本教材，而不拘泥于教材；如何創設能夠讓考生考出“真實水平”的考題是一線教育工作者不斷追求的目標，筆者根據自身多年來對初中數學教育教學的實踐和研究，采取理論與實際案例相結合的方式，揭示初中數學考題創設的“奧秘”，側重于介紹優秀考題創設的有效途徑與處理策略，從而最大程度地發揮初中數學考題的“異向”作用，為廣大初中數學教育工作者提供一點借鑒.

一、緊抓逆向思維，促進初中數學問題的“逆向化”

初中數學概念與運算通常都是成對出現且互逆的，這種對立關系形成思維的可逆性，在初中數學考題的創設中，由正向思維向逆向思維的轉變反映數學問題的題設條件與結論進行位置調換，這樣正、逆數學問題等價性的不確定也激發學生發揮雙向聯想的思維沖動，打破思維定勢的束縛，形成新的思維方法與策略.

例1在△ABC中，AD⊥BC于點D，BE⊥AC于點E，AD與BE相交于點F，如圖1所示，其中∠ABC= 45°，試求證：BF=AC.

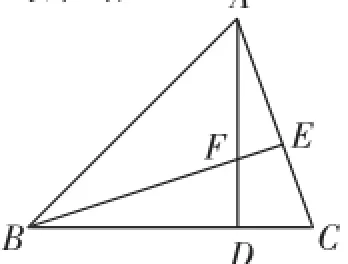
圖1

變式：已知AD與BE是△ABC中 BC與AC兩邊上的高，且交于點F，存在BF=AC，試求：∠ABC為多少？

評析：例1是課本中常見習題，題設中給定圖形，已知的條件和所要求得的結論都是確定好的，學生只要尋找證得△BFD≌△ACD即可完成解題；變式是例1題目的逆問題，要求學生根據題設內容自己思考構思畫圖及探究結論，這種題目要求學生思維的靈活性較大，由于題設中的條件具有一定的隱蔽性和迷惑性，這給學生帶來不小的麻煩，稍微不注意就會出現因疏忽題設條件而導致少解的現象，學生在思考本題時應該考慮圖1和圖2兩種情況，根據△BFD≌△ACD從而得出∠ABC=45°（圖1）和∠ABC=135°（圖2）.

此類考題可以說是源于課本但是又高于課本，學生只有具備靈活調整自身心理過程方向的能力，才能在推理過程中自如地實現反向思維的轉換，在創設逆向聯結的基礎上，實現正向與反向的融為一體化.

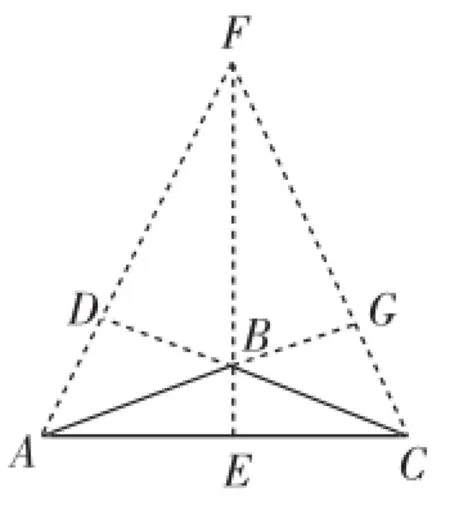
圖2

二、注重等價轉換，實現原有初中數學題型的“改頭換面”

初中數學考題經常會將常見原有題型中的條件或者問題結論，通過等價變換后讓題設條件與背景變得具有一定的隱蔽性，難以直接發現其內涵，主要目的是用來考查學生透過表象洞察初中數學問題本質的能力.

例2如圖3所示，在Rt△BAC中，AB⊥AC，AE⊥BC，∠C=60°，CD=3，則AB=_________.

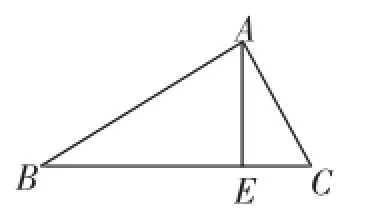
圖3

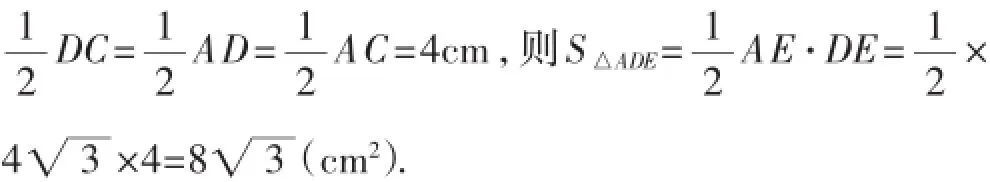
評析：將例2中原來題設中的條件進行了等價的轉

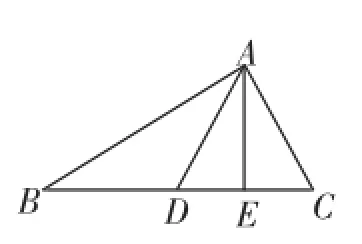
圖4

此類考題創設的目的是為了增強考查學生的思維能力和綜合分析能力，讓學生感受到考題的似曾相識之感，都能在課本試題中追尋到“原貌”，在處理的過程中，通過對這些等價轉化條件的準確辨析，實現“化新為舊、化難為易”，大大提升了數學解題的效率.

三、樹立考題“導向性、探索性”意識，助推初、高中數學的有機銜接

科技進步的過程就是人類不斷探索與創新的過程，初中數學問題的解決過程具有明顯的探索性特征，初中數學探索性問題之所以被命題者所青睞，主要是由于這類題型能夠有效地考查學生的創新思維能力與探究能力.

例3已知點P為等腰△ABC中BC邊上的任意一點，PD⊥AB于點D，PE⊥AC于點E，CF⊥AB于點F，則存在PD+PE=CF；如果點P在BC的反向延長線上，則PD、PE、CF三者之間的關系如何？

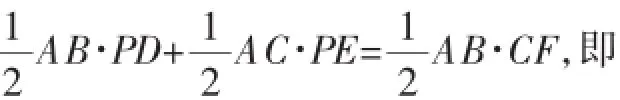
圖5

例4已知P為等邊△ABC內部的任意一點，且PD⊥BC于點D，PE⊥AB于點E，PF⊥AC于點F，則存在PD+ PE+PF等于此等邊三角形的高h；若P在等邊△ABC外部，則PD、PE、PF與高h之間的關系如何？

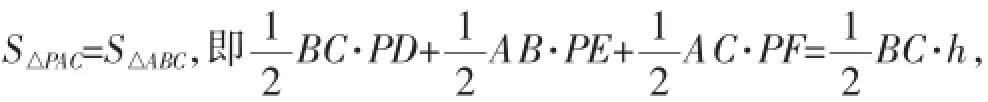
圖6

圖7

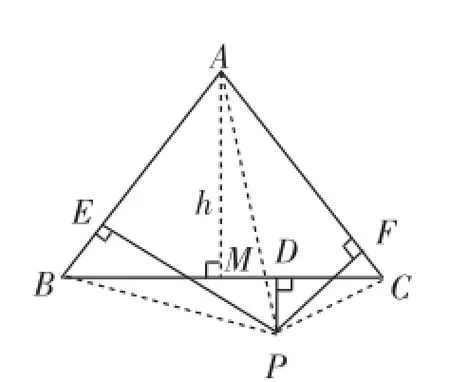
圖8

按照同樣的探索思路可以發現圖8中的面積關系為S△PAB+S△PAC-S△PBC=S△ABC，即PE+PF-PD=h.

例3與例4是兩道比較相似的探索性數學問題，一直是考題創設的熱點類型，側重于檢測學生對數學知識的理解和運用，從表面上看兩道例題具有不同的結論，但是對于高中學生而言就有所不同，由于高中已經接觸到“向量”這一利器，當利用向量來表示有向線段后就很容易發現兩道例題的結論可以進行統一；可見，此類考題中滲透著初、高中數學知識的有機銜接的氣息，體現了運動與變化、聯系與轉化、對立與統一等辯證唯物主義思想，具有很強的導向性意味和示范性作用.

總而言之，考題的創設是建立在教學大綱要求與課本教材資源相結合的基礎之上進行的，在平凡的數學知識考查中制造形式與手段、背景與情境的“奇巧與新意”，在注重考題創設的立意思想的同時，更加注重所創設的考題有助于考查學生在獨立思考的前提下創造性地分析與解決問題的能力，從而促進個性化教育、素質教育的快速形成，作為一線的初中數學教師應該在平時的教學實踐中不斷地思考與探索考題創設的方式與方法，幫助學生不斷地總結與反思，從而提升初中學生的數學解題能力.W