認知在何處？生成在何方？
——與錢德春老師商榷

☉上海市嶺南中學 劉華為

認知在何處？生成在何方？
——與錢德春老師商榷

☉上海市嶺南中學 劉華為

拜讀了錢德春老師發表在《中學數學》（下）（2014年3月）上《基于認知與生成的數學思維教學——以“三角形內角和定理”一節課為例》（以下簡稱文1）一文后，深受啟發，特別對如何從學生的認知基礎出發、從操作經驗入手、從思維受阻處突破、從“死結”打開處尋求生長點等教學智慧、技巧與方法，有了深刻認識.但也有一些不同的想法，愿與錢老師商榷.

一、商榷之點

1.學生的錯誤是否有必要逐一辨析

文1指出：“執教老師只是從圖1、圖2兩種拼圖入手，引導學生得出添輔助線的正確方法，證明了三角形內角和定理.但沒有展示圖3、圖4的拼圖，漠視了學生由這兩種拼圖得不到正確輔助線添法的困惑，失去了培養學生思維調控力的大好機遇.”

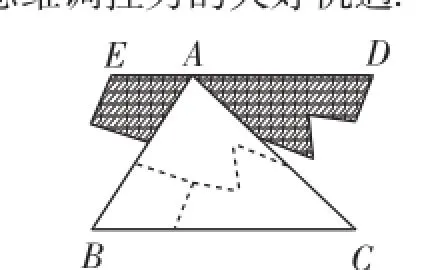
圖1

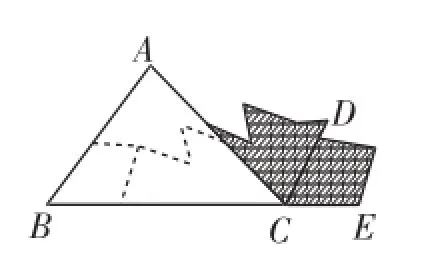
圖2

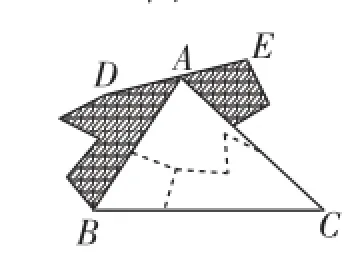
圖3

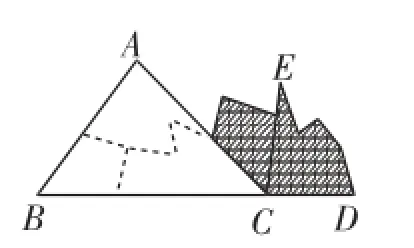
圖4

誠然，當學生在課堂上出現錯誤時，教師置之不理是教學失誤.但這是指這類錯誤已呈現在眾生面前，是一個“顯性錯誤”.根據文1可知，圖3、圖4的拼圖并沒有顯性化，是個別學生的“個性化”困惑.那么，針對這些隱性失誤，教師有沒有必要把它們一一呈現在課堂上，然后引導學生逐一辨析呢？

首先，不必說由于教學進度和時間安排引發的可行性之爭，單就必要性而言，展示、辨析圖3、圖4的拼圖也有畫蛇添足之嫌.

筆者以為，教師有必要當堂講解在巡視中發現的學生“失誤”，必須具備如下特征：第一，代表性，非少數學生的個性化行為；第二，不可解性，通過教師對問題正確處理后，其失誤學生仍然無法自悟解決；第三，可研究性，即通過進一步研究，可挖掘其“閃光點”，得到問題的不同解決方法.

顯然，圖3、圖4的“失誤”不屬此列.

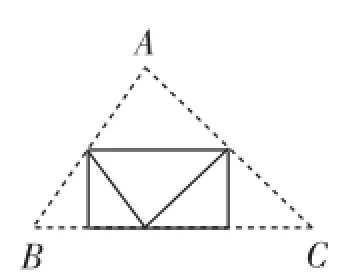
圖5

2.拼圖是本節課的重點嗎

為了能讓學生自己展示圖3、圖4，文1的建議是：給學生足夠的時間，讓學生拼圖，并充分展示他們的作品，從而歸納出圖1～圖5共五種拼圖，再逐一剖析.

其實，按照文1的拼圖要求，學生是拼不出這五種圖形的（特別地，圖5本身就不是拼出來的），因為擺在學生面前的就是從△ABC上撕下的三個角按六種方式拼成的平角圖（原△ABC已被“肢解”），對添輔助線無任何啟發，更不用說困惑了？

倒是筆者作為評委曾見過一位申報中學高級的小學老師的做法值得借鑒.執教老師在黑板上先畫出△ABC，再把與之全等的三角形紙板一分為三，涂上不同的顏色，引導學生在黑板上的△ABC處拼出了六種圖形；又引導學生用手中的三角形紙片，折疊出類似圖5的三種圖形.

理所當然，本節課獲得評委的一致好評，因為對于處于實驗幾何學習階段的小學生來說，把重點放在拼圖驗證上是亮點（特別是教師的拼圖設計為學生進入初中階段的后續學習，悄然埋下了添輔助線的伏筆，值得稱贊）.但到了突出推理的演繹幾何之初中，不惜重墨重復小學老師的做法，把拼圖仍作為教學重點是否欠妥？

當然，文1認為拼圖是教學重點還因為它是學生的認知點和添輔助線的生成點，事實果真如此嗎？

3.認知點在何處

一方面，演繹推理強調從已知條件出發，運用所學過的定義、公理和定理進行論證；另一方面，轉化思想則強調運用所學過的知識來解決新問題.因此，學生之前所學過的與180°有關的知識源于“平角的意義”和“兩直線平行同旁內角互補”才是“證明三角形內角和定理”的認知點. 4.輔助線生成在何方

若從“兩直線平行同旁內角互補”的認知點出發，作出圖6中的平行線AD是必然的.

若從“平角的意義”的認知點出發，如何利用等量轉化把∠A、∠B和∠C轉化到同一平角內是證明的突破口，而常見的等量轉化有“平移、翻折和旋轉”.因此，如何通過平移、翻折和旋轉進行角的等量轉化，才是輔助線的生成方向！據此可得圖7（旋轉——將∠B繞線段AB的中點旋轉至∠EAB處，或將∠C旋轉至∠DAC處）、圖8（平移——把∠B平移至∠EAD處）、圖9（翻折）的輔助線添法.

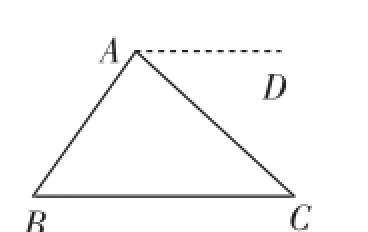
圖6

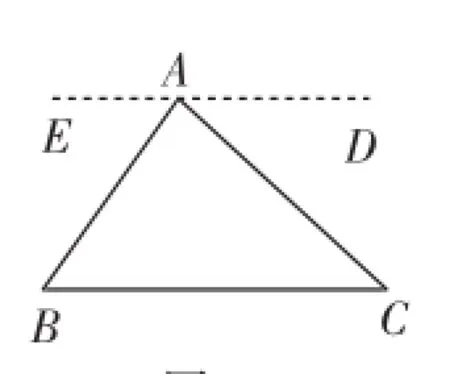
圖7

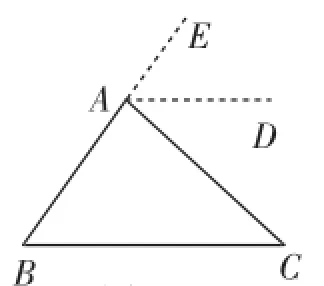
圖8

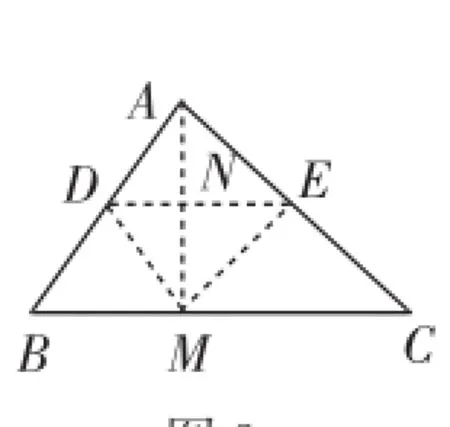
圖9

應當指出的是平移、翻折和旋轉是指效果而已，具體作輔助線時可靈活操作，否則會弄巧成拙.

如圖9的輔助線作法及其證明如下：

過點A作AM⊥BC于點M，過AM的中點N作AM的垂線，分別交邊AB、AC于點D、E，連接MD、ME.把△ADE沿直線DE翻折，由對稱性可知，點A與M重合，則∠ADE=∠MDE、∠BAC=∠DME.易知∠DNM+∠BMN=90°+90°= 180°，所以DE∥BC.得∠B=∠ADE、∠DMB=∠MDE.故∠B=∠DMB.同理可得∠C=∠EMC.又∠DMB+∠DME+∠EMC=180°，所以∠BAC+∠B+∠C=180°.

二、設計之筆

據以上，筆者認為“三角形內角和定理”的課堂教學可通過下列問題驅動：

問題1：三角形內角和是多少度？

問題2：你是怎么知道的？（度量和拼圖）

問題3：如何證明呢？（若學生難以回答，教師可作如下引導）

問題4：一般的，數學問題都是運用所學過的知識來解決的.那么，我們學過的與180°有關的知識點有哪些呢？（“平角的意義”和“兩直線平行同旁內角互補”）

至此，過頂點作其對邊的平行線，運用“兩直線平行同旁內角互補”來證明“三角形內角和定理”已是手到擒來之舉；而如何運用“平角的意義”來證明還需教師進一步啟發.

問題5：如何運用“平角的意義”來證明三角形內角和定理呢？拼圖給你什么樣的啟發？（把三角形三個內角等量轉化到同一平角內）

問題6：如何進行角的等量轉化？（教師可從角的位置變化引出圖形變換，從而得出“平移、翻折和旋轉”）

運用轉化思想來驅動問題解決的最大益處是讓學生學會如何思考，不僅知道怎樣做，更知道為什么這樣做！從而有效地突出了學法指導，強化了解決問題能力的培養.

三、題外之語

鑒于錢老師是一市之教研員，統領著一市課堂研究之方向，關于“教學失誤”，雖然形成的原因眾多，但作為一線教師，筆者想談兩點拙見，不當之處，歡迎錢老師和廣大同仁批評指正.

眾所周知，新課程實施中需突出三個力——教師課程執行力、校長課程領導力和教研員課程指導力.這三者之間的關系一目了然，既然教師執行力出現偏差，那么我們不禁要問：

1.校長的課程領導力去哪兒了

毋庸諱言，不少學校課程管理者在接待上級部門的課程調研排課時，關注點更多地落在執教人員的選擇上，常常安排一些骨干教師上展示課.殊不知，如此“精心”安排卻錯失了提升其他教師課堂教學能力的大好時機！

課程管理者若能明晰“好課是磨出來”的道理，把工作重心放在課的精心準備上，聘請學科專家引領全校同學科教師積極參與磨課，營造“暢所欲言、大膽質疑”的研討氛圍，落實“反復修改、不斷完善”的研討流程，追求“精益求精、力求完美”的研討境界，從“學情分析、教材處理、教法設計、學法指導、課堂組織和習題精選”等細節入手，把磨課真正落到實處，把好課磨到每一位教師的心里，又何必擔心由誰來執教呢？

2.教研員的課程指導力去哪兒了

據筆者所知，教研員對負責區域內教師課堂教學能力的培訓存在兩個“單一”傾向.

第一，到學校調研時，不僅獨自聽課，而且反饋也往往只與授課教師個別交流.若能拋開傳統觀念，組織區域內各校教研組長一起聽課，并進行反思性的集體研討，不僅能讓授課教師獲益匪淺，而且還能通過教研組長把研討效果輻射到轄區內的每一所學校，從而把課程指導力最大化.

第二，開展區域內公開課活動時，喜歡獨自過早地參與到課前指導中.其弊端有二：首先，束縛了授課教師及其團隊的創新力，由于教研員的特殊身份，其指導之處必然是授課教師的盲從之點；其次，阻礙了課后研討的深入交流，不難想像，教研員指導過的課，區域內的老師還敢有什么不同想法！即便有，又怎能說出口！研討活動常常會在一片叫好聲中草草收場.

筆者的想法是，既然是區域內公開課，教研員當然要參與磨課.但磨課初期，教研員應積極發揮授課教師及其團隊的作用，放任他們大膽磨課，自己只是聆聽者和思索者.等到團隊達成共識后，再組織區域內有經驗的教師或專家進行新一輪的磨課，最后展示.展示后，教研員應把整個磨課過程，結合調研時發現的問題，輔以多媒體開展一次專題講座，著重介紹磨課過程中一些教學設計取舍的背景和緣由，初稿、修改稿和定稿的優劣，本節課還可怎么處理等熱點話題.目的在于：讓教師不僅從優質課的展示中學會怎么做，還要從好課形成過程中懂得哪些不能做，以及為什么不能做.倘若如此開展公開課活動，錢老師在原文中所提到的種種“教學失誤”是否會大大減少呢？

眾所周知，突出過程教學的課程改革已如火如荼地開展了十幾年，那么，身為教研員是否也該反思：公開課活動不僅要展示結果，更要展示過程呢？

總之，當課堂教學出現“失誤”時，需反思的不應只是授課老師，還有學校的團隊、課程管理者和課程指導者.只有我們靜下心來，從學法、教法、管理和指導全方位地進行反思，積極研究對策，打造優質師資隊伍、創建高效課堂才能成為現實.如此，受益的不僅僅是老師，更有那些依在“題海”中苦苦掙扎的莘莘學子！

1.錢德春.基于認知與生成的數學思維教學——以“三角形內角和定理”一節課為例［J］.中學數學（下），2014（3）.W