靠近“最近發展區”，聚焦初中幾何特點*
——以七年級“直線、射線、線段”教學為例

☉江蘇省南通市啟秀中學 馬公仕

靠近“最近發展區”，聚焦初中幾何特點*
——以七年級“直線、射線、線段”教學為例

☉江蘇省南通市啟秀中學 馬公仕

在最近一次李庾南實驗學校教學觀摩研討活動上，筆者有幸執教了七年級“直線、射線、線段”（第1課時），得到與會老師和評課專家的贊譽，認為這節課是一節很有數學味的幾何課，靠近了學生的“最近發展區”，又體現了初中幾何的學段特點.本文整理該課的教學流程、教學片斷，并對整節課的教學立意做出闡釋，提供研討.

一、教學流程

活動一：畫圖并定義

（1）學生畫出直線、射線、線段的圖形，并研究特征.

直線：沒有端點，向兩個方向無限延伸，不能用長度單位表示長度.

射線：一個端點，能向一個方向無限延伸，不能用長度單位表示長度.

線段：有兩個端點，能用長度單位表示長度.

（2）結合圖形特征，在直線概念的基礎上定義射線、線段.

直線上的點和它一旁的部分是射線.

直線上兩點和它們之間的部分是線段.

（3）研究直線、射線、線段的表示法.

直線：直線a或直線AB（或直線BA）；

射線：射線a或射線OA（射線的端點寫在前面）；

線段：線段a或線段AB（或線段BA）.

（4）通過實踐概括直線性質和線段公理，例舉現實生活中直線性質和線段公理的例子.

學生活動，教師用PPT配合并板書，形成圖表.

活動二：練習與議論

（1）已知三點A、B、C.

①畫線段AB；②畫射線AC；③畫直線BC；④在線段BC上取一點D，連接AD.

（2）用簡潔的語言描述圖1~圖4.

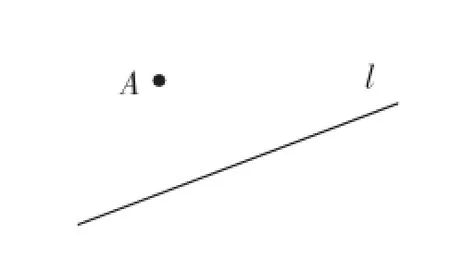
圖1

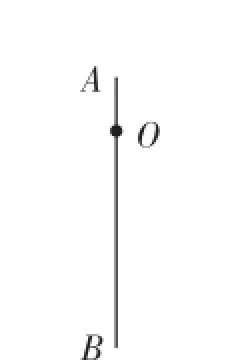
圖2

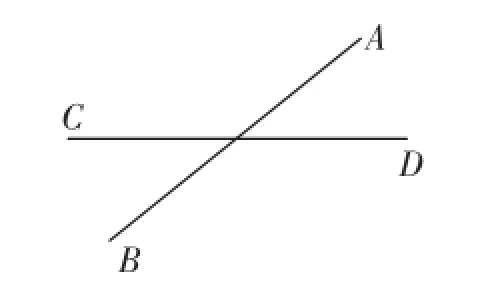
圖3

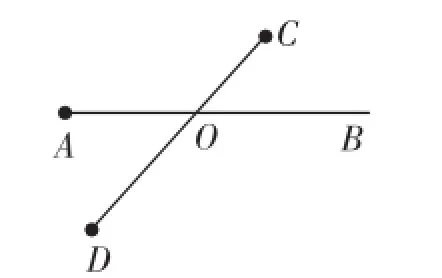
圖4

活動三：回顧與思考

（1）我們研究了哪些知識？

（2）你能體會到研究幾何圖形的方法嗎？

二、課堂片斷

片斷一：開課階段

師：上課！同學們好！我們在小學里已經對直線、射線、線段有了初步了解，今天老師將和同學們一起進一步來研究這三種圖形.（課題板書）

學生在本上畫出這三種圖形.（請一名同學上黑板，在指定區域畫，畫好回座位）

師：你說，這畫的三種圖形有什么不同？我們先來看看這條直線，所以直線是沒有界的，也就是沒有端點的，可以向兩邊無限延伸（板書：沒有端點；注意：延長和延伸不同，延伸是圖形本身，延長的部分不是圖形本身）.射線呢？（眾生：可以向一邊無限延伸）（眾生：另一邊有一個端點）線段呢？（眾生：它的兩端都有端點）所以線段是可以量出長度的，而直線與射線是不可度量的.

師：剛才我們分析了直線、射線、線段這三種圖形的不同點，其實就是它們各自的特點（板書：特點）.現在我們來研究研究這三種圖形之間有沒有聯系.（學生思考）

師：請同學們先看老師畫的圖（邊說邊演示），這是一條直線，如何表示，一般情況下，可以用一個小寫字母表示，例如直線a（標出，板書直線a）；直線a上有兩點，在平面上點用一個大寫字母表示，點A，點B，直線也可以用兩個大寫字母表示，例如：直線AB（標出AB，板書直線AB），或直線BA，當點A在直線上時，圖中除點A、點B和直線a外，有沒有出現新的幾何圖形？（有）（學生上臺講解）

學生1：線段.

師：端點是什么？這條線段如何表示？類似于直線：①用一個小寫字母表示；②用兩個大寫字母表示，所以線段也是直線的一部分，是哪一部分？

學生1：直線上兩點和它們之間的部分.

學生2：還有射線，直線上一點和它一旁的部分.

片斷二：思考三種圖形的區別和聯系

師：我們除了能表示這些圖形，知道它們的區別和聯系，還要會按要求畫圖.下面請同學們根據老師的話來畫圖，準備好了吧？

（一同學上黑板畫）①畫點A，畫直線a不過點A，在直線a上畫點O.

師：同學們看看，在同一平面內，點和直線有幾種位置關系？點A和直線a有何位置關系？點O呢？（學生分別講解）

師：繼續在這個圖上根據老師的要求畫，過點O再畫直線b，過點O再畫直線c，同學們過點O還能畫多少條直線？（無數條）.

……

片斷三：線段公理的教學

師：有A、B兩地，小明想從A地到B地，他有多少種走法？試著畫畫.哪一種走法最好？為什么？

學生公認連接兩點之間的直線段最短.

師：所有連接兩點的線中，線段最短，這是公認的（簡單的說成：兩點之間，線段最短）.我們還把連接兩點的線段的長度叫做這兩點的距離.

師：在日常生活中有哪些事例體現了線段公理.有些是正確的運用，也有一些是違反公德地運用這條性質的.你能不能舉例？（小組交流）

學生3：踐踏草坪現象.

師：古代園林建筑時，總喜歡建造曲橋，你覺得這與修建一座直的橋比，對游人觀賞湖面風光起到什么作用呢？

學生4：這樣做增加了橋的長度，一方面使這座橋能容納更多的游人來觀光，另一方面也增加了游人在橋上的行走路程，有利于游人更好地觀賞湖面風光.

三、關于教學立意的進一步闡釋

以上簡介了課例流程與課堂生成的片斷，下面就該課的備課設想再從整體上闡釋相關教學立意.

1.辨別學段特點，確立教學目標

研讀《義務教育階段數學課程標準（2011年版）》就會發現，直線、射線、線段這三種圖形在小學階段就有學習，學生并不是一張白紙走進初中幾何學習，所以辨別小學、初中不同學段對于這個教學內容的區別成為第一要務，正是基于此，我們擬定了如下的教學目標、重點及難點.

（1）了解直線、射線和線段的特征，會畫圖、會識別、會用符號表示.

（2）掌握直線的性質、線段公理和相交線，兩點間的距離等概念，并能與生活實際聯系.

（3）在訓練幾何文字語言、符號語言、畫圖語言和圖形的互化能力的過程中，體會幾何學習方法，激發學習興趣.

教學重點：直線、射線和線段的表示法、畫法和性質.

教學難點：訓練幾何文字語言、符號語言、畫圖語言和圖形的互化能力.

2.重視幾何起始教學，促進學生對幾何概念的深刻理解

眾所周知，初中幾何源于《幾何原本》，“萬丈高樓平地起”，需要重視幾何起始教學，而這個環節中，對于幾何概念（如本課時中的直線、射線、線段）的教學就需要促進學生追求深刻理解.具體來說，第一，讓學生學會用圖形語言、符號語言（包括同一種圖形的不同表征方法），并善于在不同語言之間靈活地切換、轉譯；第二，讓學生辨析直線、射線、線段之間的相同點、不同點，區別與聯系等；第三，這些概念的深刻理解，有一個表征就是學生能讀句畫圖，能根據文字語言或符號描述準確地畫出符合要求的圖形.從上面的課例中來看，我們正是在上述方向用力、花時間，而沒有過分追求所謂的練習題類型的“面面俱到”，順便提及，網上傳播的有些該課時的導學案中就常常出現學段特點辨析不清的習題（如下面的兩類題）.

習題1在邊長都是1的正方形方格紙上畫有如圖5所示的折線，它們的各段依次標著①，②，③，④，…，的序號.那么序號為24的線段長度是_________.

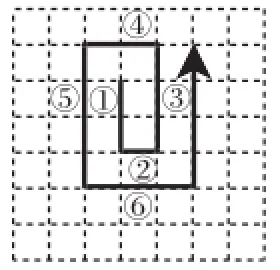
圖5

習題2某公司員工分別住在A、B、C三個住宅區，A區有30人，B區有15人，C區有10人，三個區在同一條直線上，如圖6所示，該公司的接送車打算在此間只設一個停靠點，為了使所有員工步行到停靠點的路程之和最小，那么停靠點的位置應設在（）.

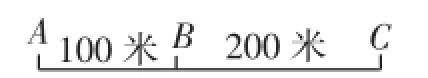
圖6

A.A區B.B區

C.C區D.A、B兩區之間

四、寫在最后

坦率地說，筆者從教二十多年，直線、射線、線段也執教過不下十次，然而這次對教學內容的定位仍然讓自己感覺到一種“常教常新”的感覺，而教學內容或重點的定位、課堂例習題或練習的精選，無不需要基于我們對幾何的深刻理解，所以“教者有怎樣的數學理解高度，就會帶給學生怎樣的數學”，這永遠不是一句空話！

致謝：本課課例從備課、試教、開課到課后反思成文，都在師傅李庾南老師的全程指導下完成的，謹致謝意！

1.中華人民共和國教育部制定.義務教育數學課程標準（2011年版）［M］.北京：北京師范大學出版社，2012.

2.李庾南.自學·議論·引導教學論［M］.北京：人民教育出版社，2013.

3.【日】佐滕學.21世紀學校改革的方向［J］.人民教育，2014（1）.

4.王光明，廖晶.“探索世界”范式及其對數學教育的啟示——ICME12獲獎報告述評［J］.課程·教材·教法，2013（12）.

5.章建躍.構建邏輯連貫的學習過程使學生學會思考［J］.數學通報，2013（6）.

*本文為江蘇省教育科學“十二五”規劃2013年度重點資助課題《“自學·議論·引導”教學生態中的學生發展質態研究》（課題編號為E-a/2013/001）的階段性成果之一，課題主持人為李庾南、王笑君．