基于初、高中銜接的“二次函數”教學

☉江蘇省徐州市第五中學 王運思

基于初、高中銜接的“二次函數”教學

☉江蘇省徐州市第五中學 王運思

函數是初等數學主要學習內容之一，它貫穿了整個中學階段的數學學習.初中數學主要學習一次函數（正比例函數）、反比例函數和二次函數，其中二次函數是初、高中函數學習的一個重要銜接點，因此做好二次函數的初、高中銜接教學至關重要.初中階段對二次函數的要求，還是立足于用代數方法來研究，比如配方、結合頂點式描述函數圖像的某些特征（開口方向、頂點坐標、對稱軸、最值）等；再比如待定系數法，通過解方程組的形式來求二次函數的解析式.少量涉及了數形結合內容，如通過畫圖像找增減性、開口方向、最大或最小值，以及通過圖像了解二次函數與坐標軸的交點及一元二次方程的根之間的關系等.可見初中對二次函數的要求相對較低，而高中的函數立足于“集合說”，函數的概念更為抽象，對函數的研究更為深入和廣泛.進入高中后，對二次函數的學習要求明顯較高，對二次函數的研究更側重于數形結合，通過圖像來研究性質，要求“數化形”及“形化數”的能力較強.那么，究竟該如何銜接好初、高中二次函數的教學，讓學生進入高中以后，能夠很快適應高中的大容量、快節奏教學方式？為此，筆者進行了一些思考與嘗試，現舉例說明如下.

一、函數圖像的平移

例1把二次函數y=x2+bx+c的圖像向上平移2個單位，再向左平移4個單位，得到函數y=x2的圖像，求b、c的值.

解法2：把二次函數y=x2+bx+c的圖像向上平移2個單位，再向左平移4個單位，得到函數y=x2的圖像，等價于把二次函數y=x2的圖像向下平移2個單位，再向右平移4個單位，得到函數y=x2+bx+c的圖像.

由于把二次函數y=x2的圖像向下平移2個單位，再向右平移4個單位，得到函數y=（x-4）2-2的圖像，即y=x2-8x+14的圖像，則函數y=x2-8x+14與函數y=x2+bx+c表示同一個函數，則b=-8，c=14.

總結：這兩種解法反映了兩種不同的思維方式，解法1是直接利用條件進行正向的思維來解決的，其運算量相對較大，解法2則是利用逆向思維，將原來的問題進行等價轉化，計算量減小，難度大大降低.“正難則反”是高中數學解題的一種技巧.

二、分類討論

例2說說二次函數y=-2x2-4x+6的圖像的相關性質.

（1）它有最值嗎？求出它的最值.

（2）當-4≤x≤-2時，求出函數的最值.

（4）通過前面三問，你能得出什么結論？

分析：此處設計是先復習基礎知識，既可以通過配方化為頂點式，說明圖像的性質，也可以畫出函數圖像，通過圖像來說性質.（1）、（2）、（3）三問分別是整個定義域、單調區間及不單調區間三種情況，讓學生感受數形結合的思想，即討論二次函數的性質，常常要借助于圖像來進行研究.而第四問，則是對上述結論作個總結.讓學生再次感受分類討論思想和數形結合思想，而這正是高中數學最常用的兩種思想.

解：（1）y=-2x2-4x+6=-2（x2+2x）+6=-2（x+1）2+8.

由-2＜0，得函數有最大值8.

（2）當-4≤x≤-2時，函數的圖像為對稱軸左邊的一段（如圖1），通過圖像可以發現，函數值是隨著自變量的增大而增大的（即是單調遞增的）.

當x=-4時，y有最小值-10；當x=-2時，y有最大值6.

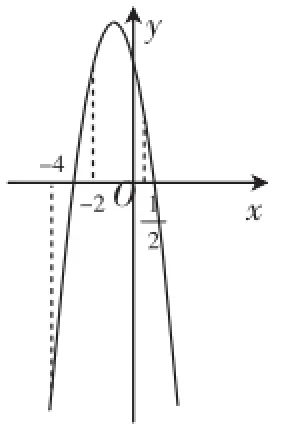
圖1

延伸：已知（-5，y1）、（-4，y2）、（-1-，y3）、（-1，y4）、（-1+，y5）、（3，y6）是函數圖像上的六點，試比較y1、y2、y3、y4、y5、y6的大小（.用“＜”連接）

例3已知函數y=x2，-2≤x≤a，其中a＞-2，求該函數的最大值與最小值，并求出函數取最大值和最小值時所對應的自變量x的值.

分析：根據函數圖像的最高點確定最大值，根據最低點確定最小值，根據最高點、最低點以及連續狀況確定y的范圍.本例中函數自變量的范圍是一個變化的范圍，圖像就是一個變化的曲線，我們需要對a的取值進行討論，來確定函數圖像的最高點與最低點.

解：（1）當-2＜a＜0時，由圖2可知：當x=-2時，函數取得最大值4；當x=a時，函數取得最小值a2.

（2）當0≤a＜2時，由圖3可知：當x=-2時，函數取得最大值4；當x=0時，函數取得最小值0.

（3）當a≥2時，由圖4可知：當x=a時，函數取得最大值a2；當x=0時，函數取得最小值0.

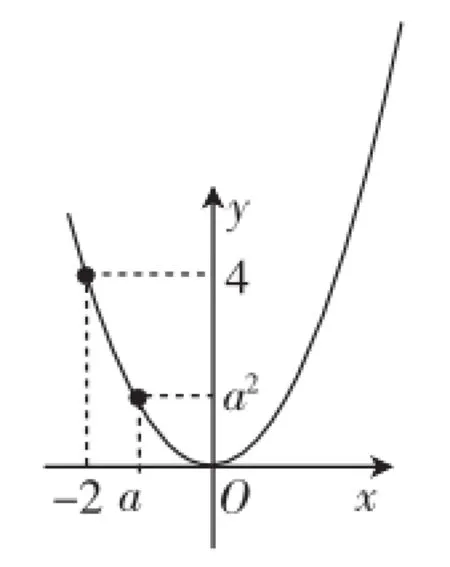
圖2

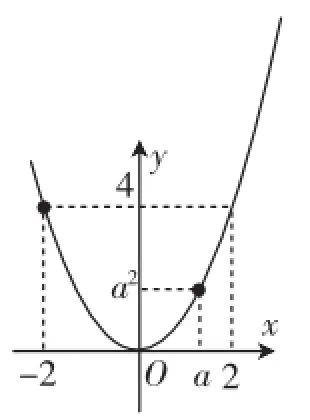
圖3

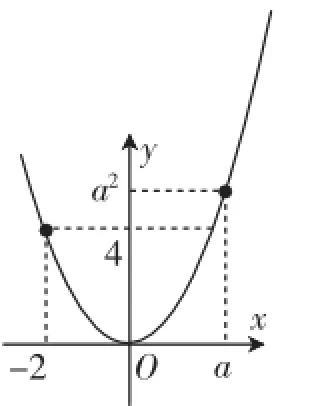
圖4

變式：已知函數y=4x2-4ax+a2-2a+2，當0≤x≤2時，函數取得最小值3，求a的值.

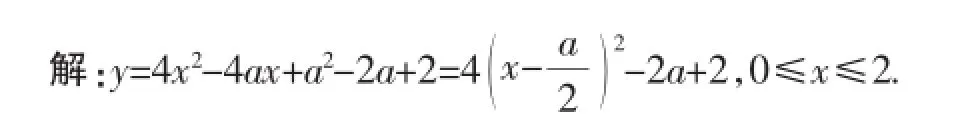
總結：高中階段對于二次函數的研究，自變量的取值往往都不是取遍所有的實數，而是在部分實數范圍內來研究.在本例中，利用了分類討論的思想，對a的所有可能情形進行討論.在解決這一類問題時，通常需要借助于函數圖像來直觀地解決問題.以開口向上的二次函數為例，根據對稱軸與x的范圍之間的關系來劃分，區間上的二次函數圖像有四種情況，如圖5.

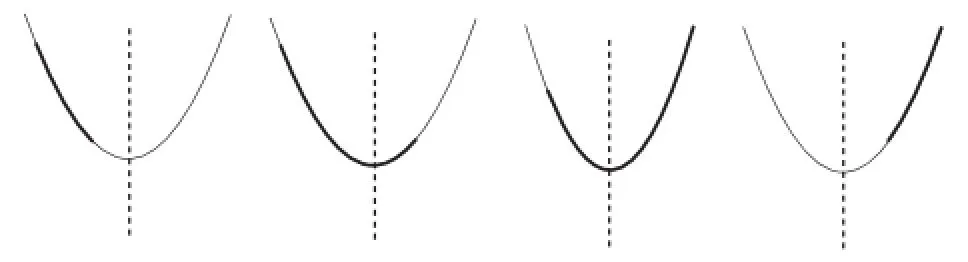
圖5

總之，二次函數在初、高中的數學教學中，具有重要地位，只有做好銜接工作，才能使學生的函數學習順暢，才能更好地進行后續的學習.