從“學不得法”談從條件尋找思維起點
——以一道試題的一題多解為例

☉江蘇省海門市貨隆初級中學 陳宏亮

從“學不得法”談從條件尋找思維起點
——以一道試題的一題多解為例

☉江蘇省海門市貨隆初級中學 陳宏亮

筆者任教的農村初中有部分學生平時學習很努力，學習習慣也很好，練習時準確率也很高，但是到考試時就是不盡如人意.這部分學生學習表現為記憶力較好，擅長文科，其學習特征是機械、呆板，理解慢，知識點總是死記硬背.因此他們基礎非常扎實，但遇到綜合性的題目就無從下手.我們總是評價他們“學不得法”，其實，這是學生思維能力欠缺的一種表現.“課程標準”指出，數學課程內容要反映社會的需要、數學的特點，要符合學生的認知規律，它不僅包括數學的結果，也包括數學結果的形成過程.同時要求教師教學時應該以學生的認知發展水平和已有的經驗為基礎.這一要求就決定了教師的教學應該注重發展學生的思維能力.本文筆者嘗試在課堂教學中利用綜合題的條件分析逐漸培養學生從條件尋找思維起點的能力，進而提高學生的思維能力.

一、例題教學過程

1.教學背景

例題是筆者所在學校初三中考一模的第27題，此題是純幾何證明（計算）題，分值為12分，班級平均得分只有1.3分，高分也只有6分.考試結束后通過與學生的交流以及對題目進行分析，發現知識點運用靈活性較大，學生的思維障礙在于做第一問時無法準確添加輔助線，而部分同學進行“嘗試性”添輔助線，嘗試很多次也無法解決，時間花了很多，但是效果不佳，因此筆者決定把例題的第一問作為突破口，引導學生從不同條件中尋找問題解決的思維切入點，達到一題多解的效果，訓練學生這方面的能力.

2.例題展示

在△ABC中，AC=BC，∠ACB=120°，點D在AB邊上，∠EDF=60°.

（1）當點D為AB的中點且∠EDF的兩邊分別交線段AC、BC于點E、F時，如圖1，求證：DE=DF.

（2）當點D不是AB的中點，且AD∶AB=1∶3時，

①若∠EDF的兩邊分別交線段AC、BC于點E、F，如圖2，求DE∶DF；

②若∠EDF的邊DE交線段AC于點E、邊DF交BC的延長線于點F，如圖3，直接寫出DE∶DF的值.

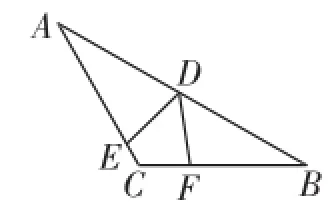
圖1

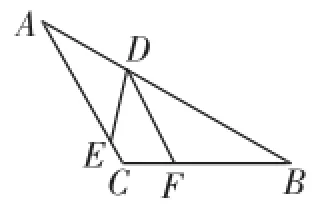
圖2

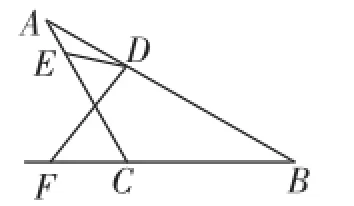
圖3

3.例題分析

幾何證明（計算）是根據一定的規則或標準，由公理和定理推導出某些命題的過程.其過程分為分析、證明、整理三個過程.分析：分析圖形的切入點及所證（求）.證明：作出輔助線，綜合運用定理、模型等方法，找出已知和未知的聯系，或推翻否定命題不成立的假設.整理：規范作答.分析過程是問題解決的重中之重，因此思維的切入點的選擇至關重要，思維起點有很多種，例如：從問題目標的特征選擇；從問題結論和解法選擇；從觀察和實驗中尋找等.而問題條件構成了問題分析的背景，通過對背景的分析還原出問題的初始形態，因此問題的條件分析是一個重要的思維起點，從這一入口進入問題的證明（計算）過程，最終得出相關結論，到達思維的終點.

問題（1）的分析如下所示.

思維起點1：在△ABC中，AC=BC，∠ACB=120°以及D為AB的中點.

分析過程：由已知條件得到∠A=∠B=30°，引導學生考慮到三角函數，但是本題中沒有直角三角形，因此需要構造，如何構造？觀察結論要證得DE=DF，需要相等