尋常之中透著不尋常
——對高中導數恒成立問題的思考

☉安徽省全椒中學 胡宗興

尋常之中透著不尋常
——對高中導數恒成立問題的思考

☉安徽省全椒中學 胡宗興

對于不等式恒成立問題，經常會涉及求參數范圍，常常需要對變量分離并將其轉化為以下兩個思路進行求解.

思路1：若m≥f（x）在x∈D上恒成立，則m≥f（x）max.

思路2：若m≤f（x）在x∈D上恒成立，則m≤f（x）min.

可見利用導數求參數范圍是不等式恒成立問題的一種重要的應用，［1］但是在解題中經常被解題人忽視，筆者由課堂上一個學生的提問，引起筆者對近幾年導數恒成立問題重新思考.

例1（2013年新課標I卷21題）已知函數f（x）=x2+ ax+b，g（x）=ex（cx+d），若曲線y=f（x）和曲線y=g（x）都過點P（0，2），且在點P處有相同的切線y=4x+2.

（Ⅰ）求a，b，c，d的值；

（Ⅱ）若x≥-2時，f（x）≤kg（x），求k的取值范圍.

解析：（I）略.

（Ⅱ）由（Ι）知a=4，b=2，c=2，d=2，所以f（x）=x2+4x+2，g（x）=2ex（x+1）.設F（x）=kg（x）-f（x）=2kex（x+1）-x2-4x-2（x≥-2），則F′（x）=2kex（x+2）-2x-4=2（x+2）（kex-1）.由題設可得F（0）≥0，即k≥1.

①若1≤k＜e2，則-2＜x1≤0.所以當x∈（-2，x1）時，F′（x）＜0；當x∈（x1，+∞）時，F′（x）＞0.即F（x）在（-2，x1）上單調遞減，在（x1，+∞）上單調遞增，故F（x）在x=x1時取得最小值，即

所以當x≥-2時，F（x）≥0，即f（x）≤kg（x）恒成立.

②若k=e2，F′（x）=2e2（x+2）（ex-e2）.所以當x≥-2時，F′（x）＞0，即F（x）在（-2，+∞）上單調遞增.又F（-2）=0，故當x≥-2時，F（x）≥0，即f（x）≤kg（x）恒成立.

③若k＞e2，則F（-2）=-2ke-2+2=-2e-2（k-e2）＜0.所以當x≥-2時，f（x）≤kg（x）不可能恒成立.綜上，k的取值范圍是［1，e2］.

說明：此解法是標準答案給出的解法，屬于構造法，學生也易想，但是對于“由題設可得F（0）≥0，即k≥1”這個問題，學生都認為考慮不到，以致問題無法進行，于是在課堂上，筆者提出這是怎么想出來的呢？緊接著就有一位同學提出想法：“可否分離參數”，筆者當時也沒有在意，隨口說了句“可以試試”，心想“答案給出是用構造法取特殊值肯定有它獨到的地方，但是既然學生提出來，又不可回避，怎么辦？”于是筆者決定在課堂上和學生一起從恒成立角度去解決，解答過程如下.

另解：（Ⅱ）由（Ι）知a=4，b=2，c=2，d=2，所以f（x）=x2+ 4x+2，g（x）=2ex（x+1）.所以f（x）≤kg（x）?2kex（x+1）≥x2+ 4x+2（x≥-2）.

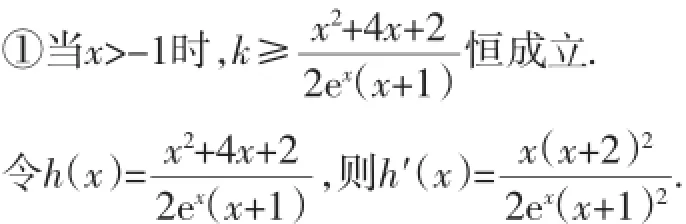
當-1＜x＜0時，h′（x）＞0，y=h（x）在（-1，0）上單調遞增；當x＞0時，h′（x）＜0，y=h（x）在（0，+∞）上單調遞減.

所以h（x）≤h（0）=1，即k≥1.

②當x=-1時，0≥-1，k∈R.

所以當-2≤x≤-1時，h′（x）＞0，y=h（x）在（-2，-1）上單調遞增，所以解得k≤e2.

綜上：1≤k≤e2.

在筆者和學生一起推理完時，教室里頓時響起了掌聲，都認為此解法符合學生的認知，且易于接受，于是筆者將其整理出來以供參考，無獨有偶，筆者在教學時又遇到一道類似的模擬題.

（Ι）如果存在x1，x2∈［0，2］，使得g（x1）-g（x2）≥M，求滿足該不等式的最大整數M.

解析：（Ι）存在x1，x2∈［0，2］，使得g（x1）-g（x2）≥M?x1，x2∈［0，2］，［g（x1）-g（x2）］max≥M.

因為g′（x）=3x2-2x-1=（3x+1）（x-1），所以當0＜x＜1時，g′（x）＜0，y=g（x）在（0，1）上單調遞減；當1＜x＜2時，g′（x）＞0，y=g（x）在（0，1）上單調遞增.

所以g（x）max=max｛g（0），g（2）｝=g（2）=1，g（x）min=g（1）=-2.所以［g（x1）-g（x2）］max=g（x）max-g（x）min=3，即M=3.

所以當a≥2時，原不等式成立，故a≥2.

所以a≥h（1）=2.

總結：以上兩題都是筆者在教學中，對區間內取特殊值問題通過轉化為恒成立問題來加以解決，其實在每年的高考中，都會有這樣的例子，例如在2014年的高考試卷中又見此類型問題，詳見如下.

例3（2014年陜西卷21題）設函數f（x）=ln（1+x），g（x）=xf′（x），x≥0，其中，f′（x）是f（x）的導函數.

（Ι）令g1（x）=g（x），gn+2（x）=g（gn（x）），n∈N+，求gn（x）的表達式；

（Ⅱ）若f（x）≥ag（x）恒成立，求實數a的取值范圍.

解析：（Ι）略.

另解：（Ⅱ）已知f（x）≥ag（x）在［0，+∞）上恒成立，所恒成立.當x=0時，滿足上式，所以a∈R.當x＞0時，恒成立.令h（x）=

筆者認為在高三正常的課堂教學中，教師不僅要關注教師的“給”，更需關注學生的“得”，要給機會讓學生大膽的講，老師充當引導者、合作者、探究者的角色，也許學生一個不經意的提問便會引起一個深刻的問題.同樣在解決問題的過程中，學生不僅要關注技巧，更應掌握通法、通解，這是提高課堂教學有效性的必備要素.