試析小學(xué)數(shù)學(xué)教學(xué)的概念引入方法

徐海燕

摘 要：小學(xué)數(shù)學(xué)教學(xué)重點在于為高層次數(shù)學(xué)學(xué)習(xí)打下堅實基礎(chǔ)，引導(dǎo)學(xué)生構(gòu)建數(shù)學(xué)思維模式，培養(yǎng)良好的數(shù)學(xué)學(xué)習(xí)習(xí)慣。概念引入方法作為小學(xué)數(shù)學(xué)教學(xué)的重點，是指導(dǎo)學(xué)生掌握正確數(shù)學(xué)知識的保障。本文筆者將結(jié)合小學(xué)數(shù)學(xué)教學(xué)過程中概念引入的重要性，探究小學(xué)數(shù)學(xué)教學(xué)的概念引入方法，以供相關(guān)人士參考。

關(guān)鍵詞：小學(xué)數(shù)學(xué);概念引入; 方法

數(shù)學(xué)概念是數(shù)學(xué)教學(xué)的基礎(chǔ)，是學(xué)生掌握知識的保障，因此，概念引入逐步成為小學(xué)數(shù)學(xué)教學(xué)中的重要環(huán)節(jié)。數(shù)學(xué)概念是影響學(xué)生整體把握知識點的關(guān)鍵，直接關(guān)系著學(xué)生思維能力、認(rèn)知能力的發(fā)展。由此可見，概念引入在小學(xué)數(shù)學(xué)教學(xué)過程中的重要性。

一、小學(xué)數(shù)學(xué)教學(xué)過程中概念引入重要性分析

一方面，概念引入可引導(dǎo)小學(xué)生正確理解和掌握數(shù)學(xué)概念，為數(shù)學(xué)學(xué)習(xí)打下堅實基礎(chǔ)。小學(xué)生好奇心強烈，欲求探索身邊的奧秘。因此小學(xué)階段是培養(yǎng)小學(xué)生數(shù)學(xué)學(xué)習(xí)興趣與良好學(xué)習(xí)習(xí)慣的關(guān)鍵時期，是引導(dǎo)學(xué)生掌握數(shù)學(xué)學(xué)習(xí)方法的重要階段。概念引入屬于概念學(xué)習(xí)的重要環(huán)節(jié)，是激發(fā)學(xué)生學(xué)習(xí)興趣的有效手段，具有承上啟下的作用，為開展有目的、有準(zhǔn)備的課堂教學(xué)提供基礎(chǔ)。

另一方面，概念引入是提高教學(xué)效率的重要措施。正確的概念引入是課堂教學(xué)活動順利、有序開展的保障，迫使學(xué)生達(dá)到融會貫通的效果。與此同時，采用適當(dāng)?shù)母拍钜敕椒ǎ粌H有利于學(xué)生掌握概念知識，提高教學(xué)效率，而且可縮短教學(xué)時間。

二、探究小學(xué)數(shù)學(xué)教學(xué)的概念引入方法

不同階段學(xué)生的認(rèn)知水平存在差異，小學(xué)數(shù)學(xué)老師應(yīng)以學(xué)生認(rèn)知水平為基礎(chǔ)，以概念形式為依據(jù)，選擇科學(xué)、合理的概念引入方法，達(dá)到教學(xué)目標(biāo)，促進(jìn)學(xué)生全面發(fā)展。

（一）觀察概念引入法

觀察概念引入法指正視概念，以觀察的視角引入概念，指導(dǎo)學(xué)生掌握概念。眾所周知，諸多小學(xué)數(shù)數(shù)學(xué)概念屬于抽象概念，學(xué)生不易掌握，但其與實際生活存在諸多聯(lián)系。因此，小學(xué)數(shù)學(xué)老師在教授相關(guān)概念時，可借助學(xué)生熟知的實物、實例等，引導(dǎo)學(xué)生仔細(xì)觀察，實現(xiàn)抽象概念具體化效果。在此基礎(chǔ)上，學(xué)生的學(xué)習(xí)積極性得以提升，致使概念學(xué)習(xí)不再受空間限制，為學(xué)生理解概念精髓提供保障。例如，在引入“角”的概念時，可借助教室里的桌子角、墻角等實物作為概念引入的媒介。在老師的指導(dǎo)下，學(xué)生通過觀察直觀形象的事物，感受“角”的特點，為學(xué)生更好的理解、掌握“角”的概念打下基礎(chǔ)，達(dá)到概念引入效果。

（二）直接概念引入法

直接概念引入法指將概念學(xué)習(xí)視為課堂教學(xué)的一個環(huán)節(jié)，直接對概念進(jìn)行講解，不需設(shè)計過多形式，主要適用于簡單概念。針對簡單概念，若過多采用生活化、情境化方式，效果并不佳，甚至出現(xiàn)適得其反，導(dǎo)致學(xué)生概念掌握模糊，造成概念間的混淆。例如，引入“有限小數(shù)”概念時，小學(xué)數(shù)學(xué)課本中對有限小數(shù)的定義如下：小數(shù)的小數(shù)部分的位數(shù)是有限的，即為有限小數(shù)。針對課本中的有限小數(shù)概念，學(xué)生通過已有知識，可準(zhǔn)確理解有限小數(shù)，進(jìn)而掌握有限小數(shù)的概念。因此，在引入有限小數(shù)概念時，老師不需設(shè)計過多教學(xué)活動。

（三）對比概念引入法

對比概念引入法，即通過對比兩個或兩個以上的概念，達(dá)到區(qū)分概念的目的，從而掌握概念含義，主要適用于易混淆概念中。在小學(xué)數(shù)學(xué)教學(xué)概念引入過程中，針對易混淆的數(shù)學(xué)概念，老師可采用對比分析的方式引入，幫助學(xué)生準(zhǔn)確掌握概念含義，避免出現(xiàn)概念混淆的狀況。例如，引入“正比例”概念與“反比例”概念時，老師采用對比分析的方式開展概念引入教學(xué)活動，引導(dǎo)學(xué)生發(fā)現(xiàn)“正比例”與“反比例”的異同點，幫助學(xué)生掌握兩者的含義，避免造成兩者混淆，使學(xué)生的區(qū)分能力得到提升。

（四）剖析概念引入法

剖析概念引入法主要適用于較復(fù)雜的概念，即在數(shù)學(xué)老師的指導(dǎo)下，深入剖析概念，緊扣概念核心和性質(zhì)特征，做到循序漸進(jìn)，引導(dǎo)學(xué)生理清思路，掌握概念。針對“四則運算”概念，屬于小學(xué)數(shù)學(xué)相對復(fù)雜的概念。因此，在引入四則運算概念時，避免好高騖遠(yuǎn)，堅持循序漸進(jìn)的原則，緊扣“一級運算”、“二級運算”以及“括號”，把握三者的內(nèi)在關(guān)系，進(jìn)而分析、理解四則運算概念。

（五）圖解概念引入法

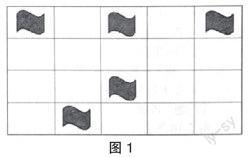
圖解概念引入法主要針對抽象概念而言，借助具體圖形，變抽象為具體，幫助學(xué)生掌握抽象概念。數(shù)學(xué)學(xué)科具有抽象性強、邏輯性高的特點，要求學(xué)生具備較高的抽象思維能力。針對小學(xué)生而言，其抽象思維能力發(fā)展尚不完善，仍以形象思維為主，導(dǎo)致學(xué)生理解抽象數(shù)學(xué)概念存在較大困難。因此，小學(xué)數(shù)學(xué)引入抽象概念時，老師應(yīng)適當(dāng)轉(zhuǎn)換抽象概念，借助具體可感的圖形，幫助學(xué)生理解概念，進(jìn)而達(dá)到掌握抽象概念的目的。例如，引入“平移”概念時，平移屬于“圖形與變換”單元，在引入該概念時，可借助圖形，老師在黑板上上畫一個格子圖（如圖1），并在格子中畫幾個旗子，讓學(xué)生思考如何平移旗子以達(dá)到幾個旗子重合。在具體演示基礎(chǔ)上，學(xué)生經(jīng)過觀察和討論，得到并理解平移的概念，即物體沿著一條直線移動，方向并未發(fā)生變化。

圖1

三、結(jié)語

總而言之，概念教學(xué)是小學(xué)數(shù)學(xué)教學(xué)的重難點，是促使學(xué)生掌握數(shù)學(xué)學(xué)習(xí)方法的有效手段，有利于提高學(xué)生解決問題的能力。與此同時，數(shù)學(xué)概念作為小學(xué)數(shù)學(xué)學(xué)習(xí)的基礎(chǔ)，是學(xué)生高層次數(shù)學(xué)學(xué)習(xí)的前提。因此，小學(xué)數(shù)學(xué)教學(xué)概念引入過程中，小學(xué)數(shù)學(xué)老師應(yīng)以學(xué)生認(rèn)知水平為依據(jù)，選擇科學(xué)的概念引入方法，激發(fā)學(xué)生數(shù)學(xué)學(xué)習(xí)積極性，促使學(xué)生養(yǎng)成良好的數(shù)學(xué)學(xué)習(xí)習(xí)慣，引導(dǎo)學(xué)生掌握正確的數(shù)學(xué)學(xué)習(xí)方法，促進(jìn)學(xué)生全面發(fā)展。

參考文獻(xiàn)：

[1]李曉. 小學(xué)數(shù)學(xué)教學(xué)中概念引入的方法探究[J]. 科學(xué)中國人，2015，06：196.

[2]于慧. 小學(xué)數(shù)學(xué)教學(xué)中概念引入的方法探究[J]. 讀書文摘，2015，16：164.

[3]黃海云. 小學(xué)數(shù)學(xué)教學(xué)中概念引入的方法探究[J]. 考試周刊，2015，52：65.

[4]馮常艷. 小學(xué)數(shù)學(xué)教學(xué)中概念引入的方法探究[J]. 基礎(chǔ)教育研究，2013，03：40-41..