一道高中數學聯賽試題的探究與發現

●吳建山 (龍海市第二中學 福建龍海 363110)

一道高中數學聯賽試題的探究與發現

●吳建山 (龍海市第二中學 福建龍海 363110)

題目給定橢圓C：⊙O：x2+y2=b2，自橢圓上異于其頂點的任意一點P作⊙O的2條切線，切點分別為M，N，若直線MN在x軸、y軸上的截距分別為m，n，證明

(2010年全國高中數學聯賽江西省預賽試題)

1 探索

試卷提供的解法較為繁瑣，且技巧性較高.其實，運用“設而不求”的數學思想，容易得到本題的如下簡潔證法.

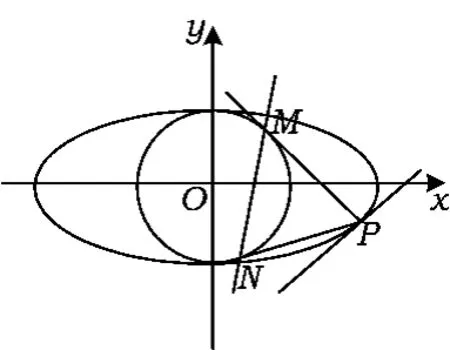
圖1

證明如圖1，設 P(x0，y0)，M(x1，y1)，N(x2，y2)，則2條切線PM，PN的方程分別為

x1x+y1y=b2，x2x+y2y=b2.由點P在2條切線上，知

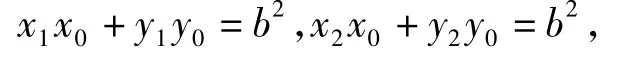
因此直線MN的方程為

2 發現

若對圖形作探究，不難發現，隨著點P的運動，橢圓在點P處的切線與切點弦都作相應變化，它們的斜率之間是否存在某種內在聯系呢?由以上的證明可知，切點弦MN的斜率為而橢圓在點P處的切線方程為

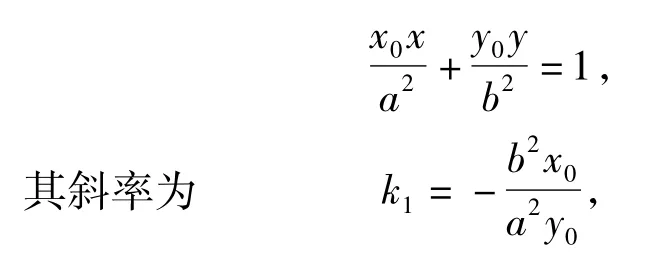
3 拓展

將上述結論拓廣至橢圓與雙曲線，以及圓與雙曲線，可得如下有趣性質.

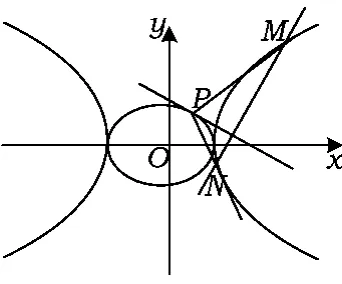
圖2

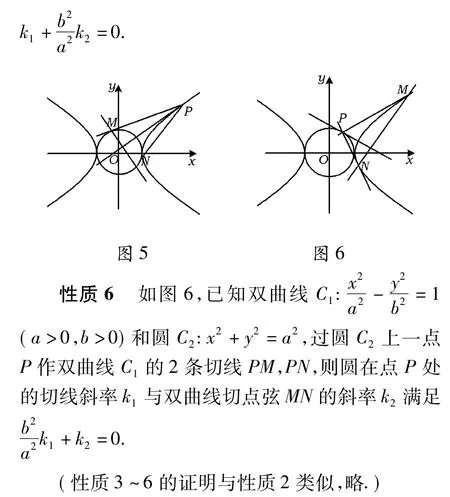
［1］林新建.“情侶圓錐曲線”的有趣性質及其拓廣［J］.數學通報，2010(7)：58-60.

［2］玉云化.共焦點的圓錐曲線的切線性質［J］.數學通訊，2009(3)：27-28.