一道競賽題的探究

●徐文春 (常州高級中學 江蘇常州 213003)

一道競賽題的探究

●徐文春 (常州高級中學 江蘇常州 213003)

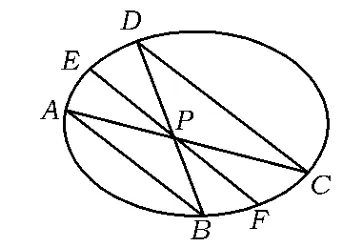
圖1

(1)證明：直線AB的斜率為定值;

(2)過點P作AB的平行線，與橢圓交于點E，F，證明：點P平分EF.

(2013年全國高中數學聯賽湖北省預賽高二試題)

1 本質解讀

此題考查橢圓中相交弦的性質，滲透著圓錐曲線與直線的基本知識和方法，試題簡潔，結論優美且具一般性.試題第(2)小題與圓錐曲線中的坎迪定理相關，筆者猜想試題的命制是以坎迪定理為背景.

在文獻［1］中，坎迪定理在橢圓中有如下推廣：

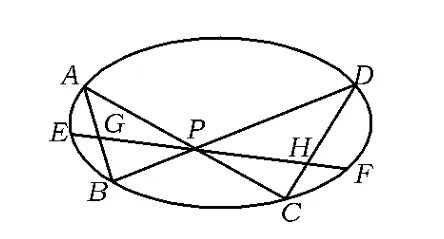
圖2

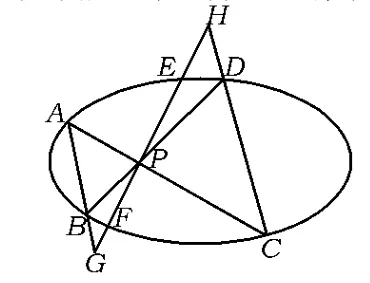
圖3

定理如圖2，蝶形ABCD內接于橢圓Γ，BD，AC的相交于點P，過點P作直線EF分別交AB，CD于點 G，H，交橢圓Γ 于點 E，F，則

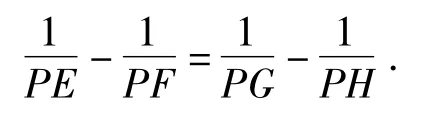
由定理的證明可知，當AB∥CD時，直線EF位置如圖3所示時，結論仍成立.若直線EF繼續旋轉至與AB，CD平行，此時可看作它們交于無窮遠處，也即PG，PH為無窮大，得PE=PF.該題本質上是圓錐曲線中坎迪定理的一種極限情形，在第(2)小題基礎上由圓錐曲線的中點弦性質也可得出第(1)小題的結論，或許為了降低難度，命題時添加了第(1)小題.

實際上，與EF平行的弦都被直線PO平分，再由平行線性質知，圖4中夾在直線與橢圓間的線段EM=FN，結合平面上的祖暅原理立得如下有趣性質：

性質2 如圖4，條件同性質1，則曲邊三角形PAD與PBC面積相等.

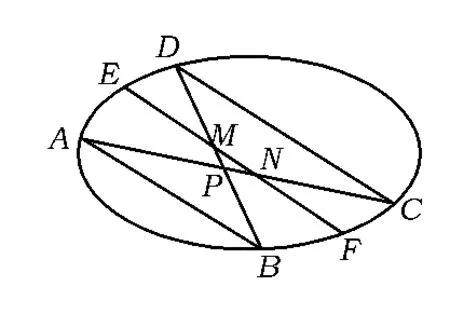
圖4

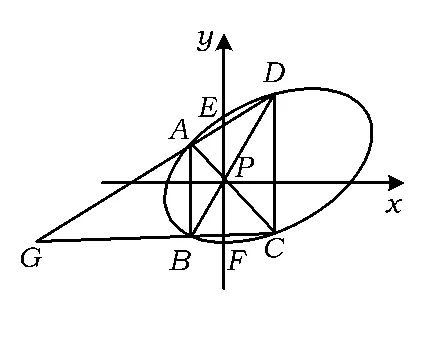
圖5

性質3如圖5，設P為橢圓Γ內一定點(非橢圓中心)，過點P的2條直線分別與橢圓交于點A，C 和 B，D，若 AB∥CD，則直線 BC，AD 的交點為定點.

證明為了簡化證明過程，以P為原點、以EF所在直線為y軸建立如圖5所示的直角坐標系.設橢圓的方程為

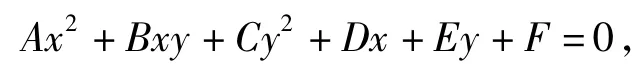
設 E(0，t)，F(0，－t)知 t，－t是 Cy2+Ey+F=0的2個根，從而E=0.

一方面，由題知直線AC，BD的斜率存在，可設A(x1，k1x1)，B(x1，k2x1)，C(x2，k1x2) 和 D(x2，

k2x2)，則直線DA的方程為

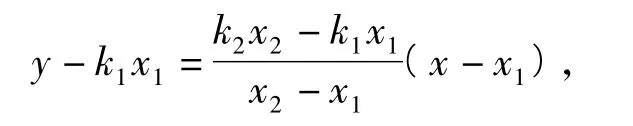
直線CB的方程為

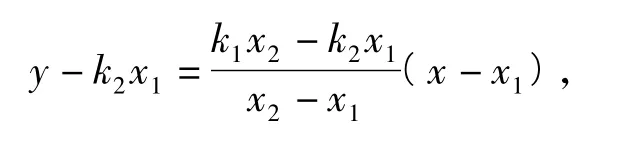
聯立方程消去y，化簡整理得

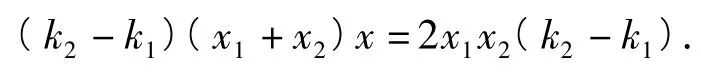
又由題設條件和橢圓對稱性知

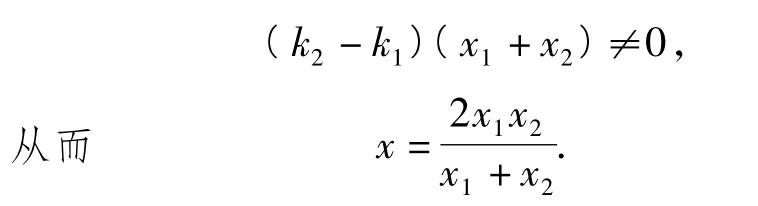
另聯立橢圓方程Ax2+Bxy+Cy2+Dx+F=0和直線AC方程y=k1x，得

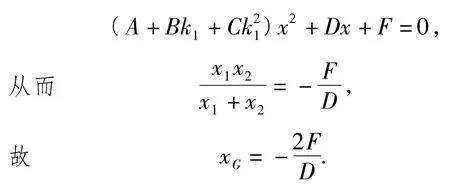
另一方面，因為A(x1，k1x1)在橢圓上，所以

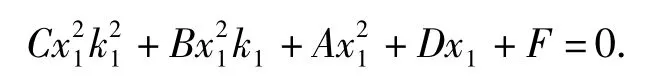
同理 B(x1，k2x1)也在橢圓上，得

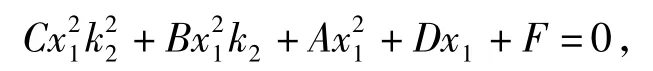
故k1，k2可看作關于k的方程

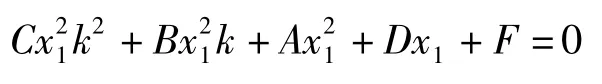
的2個根，即得

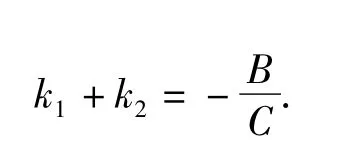
又由平行線性質知點G，P與線段AB，CD的中點共線，也即點G在直線上，從而

在性質3中，當點A，D無限接近時，橢圓的割線就變為在點E處的切線，因此上述中的定點G即是橢圓在點E，F處切線的交點.

［1］段惠民，饒慶生.坎迪定理在圓錐曲線上的推廣［J］.中學數學研究，2007(3)：17.