2014年高考復(fù)習(xí)中空間幾何體的關(guān)注點

●楊 平 胡 芳 楊海蘭 (日壇中學(xué) 北京 100025)

2014年高考復(fù)習(xí)中空間幾何體的關(guān)注點

●楊 平 胡 芳 楊海蘭 (日壇中學(xué) 北京 100025)

高考中的多面體考什么?《普通高中數(shù)學(xué)課程標(biāo)準(zhǔn)》指出，幾何學(xué)是研究現(xiàn)實世界中物體的形狀、大小與位置關(guān)系的學(xué)科.人們通常采用直觀感知、操作確認(rèn)、思辨論證、度量計算等方法認(rèn)識和探索幾何圖形及其性質(zhì).三維空間是人類生存的現(xiàn)實空間，認(rèn)識空間圖形，并培養(yǎng)和發(fā)展學(xué)生的空間想像能力、推理論證能力、運用圖形語言進(jìn)行交流的能力以及幾何直觀能力，是高中階段數(shù)學(xué)課程的基本要求.影響幾何體形狀的垂直與平行及其大小的面積與體積、角與距離是必考的內(nèi)容.

1 影響幾何體形狀的元素——垂直與平行

在空間點、線、面位置關(guān)系問題中，涉及到的垂直與平行元素很多，如線線垂直(有相交線垂直，還有異面直線垂直)、線面垂直、面面垂直;有線線平行、線面平行和面面平行，這些垂直與平行元素又導(dǎo)致幾何體的形狀特征很特殊，因此，在幾何體中研究垂直與平行的價值也就顯得更有意義了.

在歷年數(shù)學(xué)高考中，垂直與平行元素是必考的內(nèi)容之一.

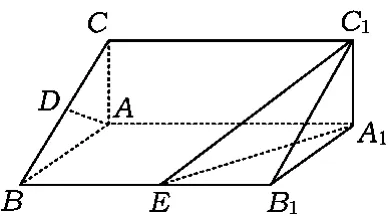
圖1

例1如圖1，在直棱柱ABC-A1B1C1中，是BC的中點，點 E在棱BB1上運動.證明：AD⊥C1E.

(2013年湖南省數(shù)學(xué)高考文科試題改編)

解因為 E為動點，所以需證 AD⊥平面CBB1C1.因為 ABC-A1B1C1是直棱柱，所以 BB1⊥平面ABC，且AD?平面ABC，得BB1⊥AD.又因為△ABC是等腰直角三角形且D為BC的中點，所以BC⊥AD，從而 AD⊥平面 CBB1C1，又 C1E?面CBB1C1，得 AD⊥C1E.

評注此題背景是直三棱柱，直接問題是直線與直線垂直問題，一般通過直線與平面垂直來解決，尤其是異面直線的垂直問題.另外，此題有個隱含條件，即點E在棱BB1上運動，說明C1E是動直線，若要AD與動直線C1E垂直，則AD就需與C1E掃過的平面BCC1B1垂直.

例2如圖2，在四棱錐P-ABCD中，∠ABC=∠BAD=90°，BC=2AD，△PAB與△PAD都是邊長為2的等邊三角形.證明：PB⊥CD.

(2013年全國數(shù)學(xué)高考大綱卷文科試題改編)

證明取BC的中點E，聯(lián)結(jié)DE，則ABED為正方形.過點P作PO⊥平面ABCD，垂足為O.

聯(lián)結(jié)OA，OB，OD，OE，因為△PAB 和△PAD 都是等邊三角形，知PA=PB=PD，所以O(shè)A=OB=OD，即點 O為正方形 ABED對角線的交點，故OE⊥BD，從而PB⊥OE.因為O是BD的中點，E是BC的中點，所以O(shè)E∥CD，從而PB⊥CD.

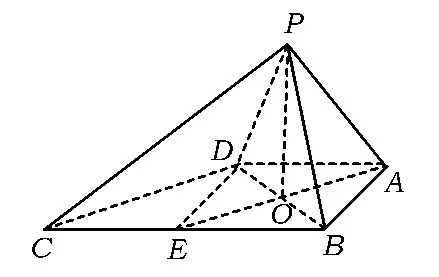
圖2

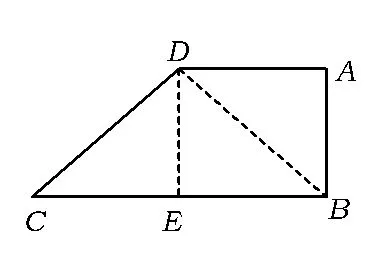
圖3

評注這個幾何體看似不規(guī)則，也沒有一條側(cè)棱垂直于底面的特征.我們先研究一下底面(如圖3)，這是一個特殊的直角梯形，有垂直、平行的元素，還有正方形、等腰直角三角形等信息;另外，由題意可得，PA=PB=PD，說明點P在平面ABD上的射影落在△ABD的外心，即Rt△ABD的斜邊的中點O.

這個四棱錐P-ABCD也可以是由一個正四棱錐P-ABED和一個三棱錐P-CDE組合而成.

例3如圖4，在等腰直角三角形ABC中，∠A=90°，BC=6，D，E 分別是 AC，AB 上的點，，O為BC的中點.將△ADE沿DE折起，得到如圖5所示的四棱錐A'-BCDE，其中A'O=.證明：A'O⊥平面 BCDE.

(2013年廣東省數(shù)學(xué)高考理科試題改編)

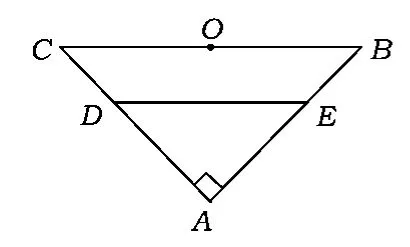
圖4

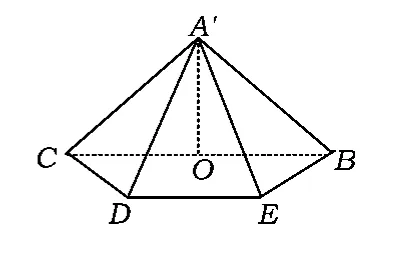
圖5

分析這是一個翻折問題，翻折后得到四棱錐A'-BCDE，翻折后的最終結(jié)果是側(cè)面 A'CB⊥面BCDE，怎樣才能保證平面與平面垂直呢?這里隱含著A'O⊥平面BCDE，也就是點A'在平面BCDE上的射影落在BC的中點O上.

在翻折前后的不變量有：

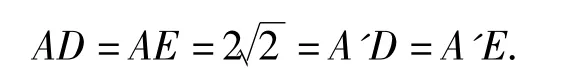
因為O是BC的中點，故等腰直角三角形△ABC中，OE=OD，所以△A'OD≌△A'OE.如圖 4，在，由余弦定理可得所以

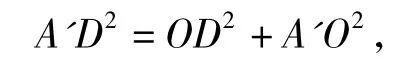
得A'O⊥OD，同理可得 A'O⊥OE，故 A'O⊥平面BCDE.

不難發(fā)現(xiàn)，考題中給出的幾何體中有三棱錐、四棱錐、三棱柱、四棱柱，有的棱錐有一條側(cè)棱垂直于底面，有的棱錐是正棱錐與其他棱錐的組合體;柱體中有直棱柱，還有斜棱柱;幾何體的底面也是形形色色的.這些都只是載體而已，在內(nèi)涵豐富的幾何體中，巧妙地把影響空間幾何體形狀的垂直和平行元素蘊含其中，既能考查空間想象能力，又能考查推理論證能力.

2 幾何體大小的研究對象——面積與體積、角與距離

除了關(guān)心幾何體的形狀外，我們還關(guān)心其大小，常見的大小就是面積與體積、角與距離，涉及到的幾何體均為柱、錐、臺體或其簡單的組合體.

2.1 面積與體積

準(zhǔn)確記憶體積公式并觀察幾何體的特征(形狀)，進(jìn)而找到相應(yīng)的數(shù)量關(guān)系，是準(zhǔn)確求解面積與體積問題的關(guān)鍵.

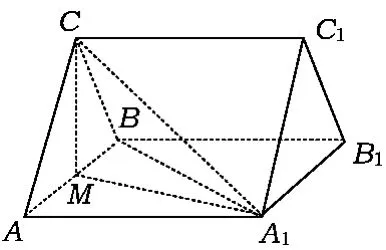
圖6

例4如圖6，在三棱柱 ABC-A1B1C1中，CA=CB，AB=AA1，∠BAA1=60°.

(1)證明：AB⊥A1C;

(2013年數(shù)學(xué)高考課標(biāo)卷文科試題)

(1)略.

(2)解取 AB的中點 M，聯(lián)結(jié) MC，MA1，△ABC與△A1AB都是邊長為2的等邊三角形，故

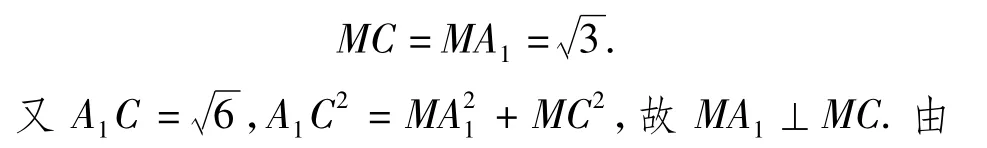
評注此題的背景為斜三棱柱，由于有第(1)小題的鋪墊，即垂直的元素很多，故找此三棱柱的高相對容易一些.而三棱錐C-ABA1是一個常見的空間四邊形模型，即共底等腰三角形，CA=CB，A1A=A1B，常見的處理方法是取底邊AB的中點M，聯(lián)結(jié) MC，MA1，進(jìn)而證明 AB⊥平面 MCA1.

2.2 角與距離

由于向量的引入，使得空間的角(線線角、線面角、面面角)，以及距離就顯得輕松了.

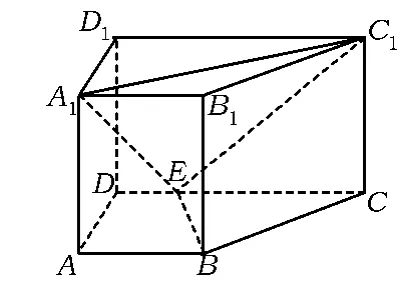
圖7

例5如圖7，在直四棱柱 ABCD-A1B1C1D1中，AB∥CD，AD⊥AB，AB=2，AD=，AA1=3，E 為 CD 上一點，DE=1，EC=3.求點 B1到平面EA1C1的距離.

(2013年江西省數(shù)學(xué)高考文科試題改編)

評注這是一個空間點到平面的距離問題，通常的方法為等體積法或向量法，因為此三棱錐恰好在直三棱柱中，且一個面A1B1C1恰位于棱柱的底面，頂點E在另一個底面上，故易求體積，可以考慮用等體積方法;另外，這個幾何體為直四棱柱，且，適合建立空間直角坐標(biāo)系，用向量法求解亦很簡單.

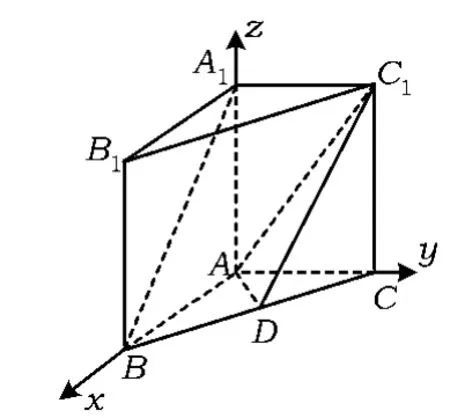
圖8

例6如圖8，在直三棱柱 A1B1C1-ABC中，AB⊥AC，AB=AC=2，AA1=4，點D是BC的中點.

(1)求異面直線 A1B與C1D所成角的余弦值;

(2)求平面ADC1與平面ABA1所成二面角的正弦值.

(2013年江蘇省數(shù)學(xué)高考試題)

分析此幾何體為直三棱柱，且 AB⊥AC，AB=AC=2，AA1=4，適合建立空間直角坐標(biāo)系，并且圖中各點均易得到坐標(biāo).

解(1)以A為原點、AB所在直線為x軸、AC所在直線為y軸、AA1所在直線為z軸建立空間直角坐標(biāo)系，則 A1(0，0，4)，C1(0，2，4)，A(0，0，0)，B(2，0，0)，C(0，2，0)，D(1，1，0)，故

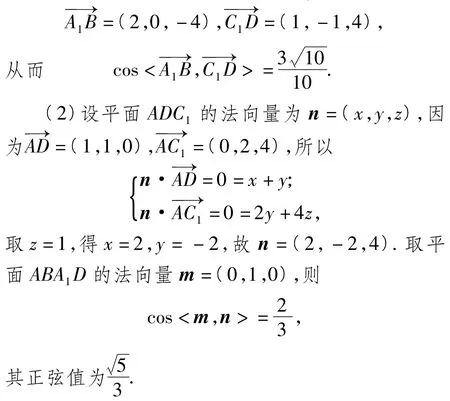
評注向量法是求解立體幾何中的角的問題、距離問題的好方法，思路簡潔清晰，建立恰當(dāng)?shù)目臻g直角坐標(biāo)系是關(guān)鍵.

3 空間直角坐標(biāo)系中幾何體的點的坐標(biāo)與法向量

用向量法求解固然簡單，但建立空間直角坐標(biāo)系后，有些運算需要用到的點卻不易求出，導(dǎo)致相應(yīng)的向量求不出，影響了解題，怎么辦?其實解決起來很簡單，即利用向量相等的定義，找到與所求向量相等且易求的向量坐標(biāo)，而有些動點的坐標(biāo)可利用向量共線的充要條件求解.

例 7如圖 9，在三棱柱ABC-A1B1C1中，AA1C1C是邊長為4的正方形，平面 ABC⊥平面AA1C1C，AB=3，BC=5.

(1)求證：AA1⊥平面ABC;

(2)求二面角A1-BC1-B1的余弦值;

(3)證明：在線段BC1上存在點D，使得AD⊥A1B，并求的值.

(2013年北京市數(shù)學(xué)高考理科試題)

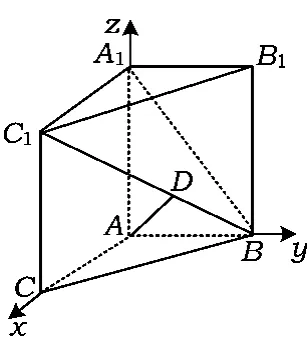
圖9

(1)(2)略.

(3)證明以A為原點、AC所在直線為x軸、AB所在直線為y軸、AA1所在直線為z軸建立空間直角坐標(biāo)系，則B(0，3，0)，C1(4，0，4)，A1(0，0，4).設(shè)D(x，y，z)是直線 BC1上的一點，

如何找空間一點的坐標(biāo)呢?點 A1，C1，B，B1均在坐標(biāo)平面上，其坐標(biāo)相對容易找到，而點D不在坐標(biāo)平面上，就不易找了.注意到一個重要條件：即點D是線段BC1上的動點，由此確定求點D的方案.

方案1求出BC1的方程，進(jìn)而表示出點D的坐標(biāo)，但不易實施，因為空間直線方程不好求，需找平面的交線.

方案2利用點D在BC1上，利用三點共線的充要條件，以向量法求解.

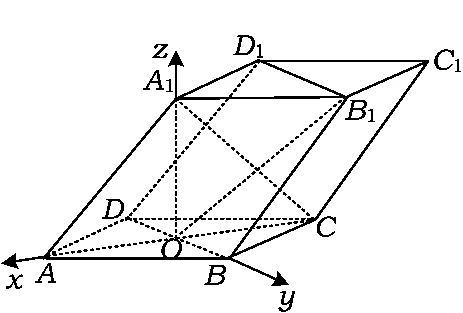
圖10

例8如圖10，四棱柱ABCD-A1B1C1D1的底面ABCD是正方形，O為底面中心，A1O⊥平面

(1)證明：A1C⊥平面BB1D1D;

(2)求平面OCB1與平面BB1D1D的夾角θ的大小.

(2013年陜西省數(shù)學(xué)高考理科試題)

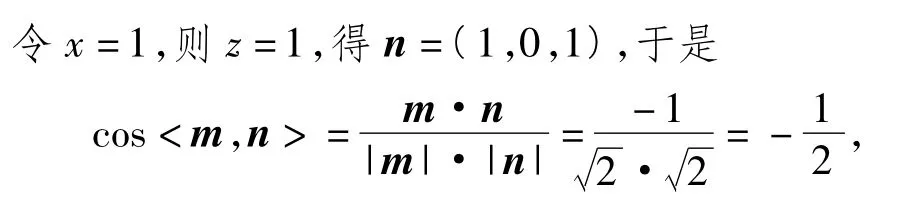
易知平面OCB1與平面BB1D1D的夾角θ為銳角，因此 θ=60°.

評注此幾何體中，點 O，A，B，C，D，A1的坐標(biāo)易求，但點B1的坐標(biāo)不易求，而在找平面OCB1的法向量時，必須用到點B1的坐標(biāo)，這個問題是好解決的，因為求法向量時真正用的是向量而不是點B1的坐標(biāo)，我們發(fā)現(xiàn)的坐標(biāo)易求，同理可得可以用來求.

為了準(zhǔn)確快速求解幾何體問題，筆者建議：(1)要對形形色色的底面多邊形注意研究，如常見的梯形、菱形、等腰三角形，解題時可以將此多邊形移出幾何體，畫出平面圖形，找到涉及的平行與垂直元素、數(shù)量關(guān)系;(2)熟練掌握常見幾何體的性質(zhì)，如正棱錐、直棱柱、正方體、正四面體以及4個面都是直角三角形的四面體;(3)理解概念本質(zhì)，才能以不變的知識應(yīng)對百變的試題.