基于奇異值分解和相關峭度的滾動軸承故障診斷方法研究

張永祥，王孝霖，張 帥，朱杰平

(海軍工程大學 動力工程學院, 武漢 430033)

滾動軸承在各類旋轉機械中應用廣泛，是機械設備的關鍵零部件，也是易損元件。振動監測法適用于各種類型和工況的軸承，且適于早期故障監測和在線監測，是常用的滾動軸承故障監測診斷方法。滾動軸承的工作環境一般包含很多其它機械零部件，檢測信號中存在諸如機器不平衡產生的振動、齒輪嚙合振動等強背景噪聲，滾動軸承輕微故障的特征信息往往淹沒在背景噪聲中，很難被發現和提取出來。

近年來，眾多學者對軸承的故障診斷進行了廣泛研究[1]，常用方法的核心集中于消噪和特征提取。小波分析在原信號中故障沖擊相對明顯時，可以獲得更為明顯、可以確認的時域沖擊特征，但是小波分析的頻帶特性使其難以對微弱故障特征進行有效提取[2]。奇異值分解(SVD)近年來在信號的處理分析中獲得了重要的應用，在特征信息分離和弱信號提取方面取得了良好的效果[2-3]。Hankel矩陣方式下的SVD分量信號具有線性疊加特性，通過選取感興趣的分量進行疊加，可以實現對信號特征信息的提取[4]。利用SVD分離出的分量信號進行特征提取時，關鍵在于有用分量的確定，分量的選擇影響信號處理的效果。

本文首先分析了Hankel矩陣方式下SVD的信號分解原理，指出其信號分解的實質是一種線性疊加分解[4]。隨后，引入了相關峭度的概念，并對相關峭度的定義進行了闡述[5]。對SVD的特征提取方法進行研究，結合軸承振動信號的特點，提出了根據相關峭度進行SVD分量信號選擇的軸承故障特征提取方法。對滾動軸承故障沖擊振動信號展開研究，通過仿真信號和工程實測的滾動軸承振動信號對該方法的有效性進行驗證。

1 SVD的信號分解和特征提取

1.1 SVD的信號分解原理

奇異值分解是指[6]：對于一個實矩陣A∈Rm×n，必定存在正交矩陣U∈Rm×n和正交矩陣V∈Rn×n，使得(1)成立

A=UDVT

(1)

式中，D為對角陣，D∈Rm×n，可表示為D=[diag(σ1,σ2,…,σq)O]或者其轉置，這取決于m≤n還是m>n，O表示零矩陣，q=min(m,n)，且有σ1≥σ2≥…≥σq≥0，它們稱為矩陣A的奇異值。

對于一個一維信號序列，為了利用SVD對其進行處理，必須先利用信號構造出一個矩陣。設有離散數字信號X=[x(1),x(2),…,x(N)]，利用此信號可以構造Hankel矩陣[7]。

為了利用SVD實現信號的分離，需將式(1)改寫成用列向量ui和vi表示的形式

(2)

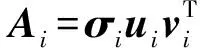
(3)

從Hankel矩陣的構造過程可知，只要將Ai的第一個行向量Pi,1=[xi(1)xi(2) …xi(n)]和最后一個列向量中第2行至m行元素組成的向量Hi,n=[xi(n+1)xi(n+2) …xi(N)]首尾相接，就可以構成一個分量信號Si，寫成向量形式為

Si=[Pi,1Hi,n]Pi,1∈R1×n,Hi,1∈R1×(m-1)

(4)

全部Ai(i=1,2,…,1)按照此方式構成的分量Si就形成了對原始信號的一種分解，分量信號的順序根據相應奇異值σi的大小從高到底依次排列。這q個分量信號的線性疊加的結果就是原始信號，即

S1+S2+…+Sq=X

(5)

由以上過程可知，SVD可以將原始信號分解為一系列分量信號的簡單線性疊加。利用這種線性疊加關系，通過選取合適的分量，可以實現對信號特征信息的提取。

1.2 矩陣結構的確定

Hankel矩陣構造時，m和n的取值不同，SVD的信號分解效果會有很大區別。可以通過對信息量變化趨勢進行分析，進而確定合理的矩陣結構。

各分量信號Si包含的信息量是彼此不同的，具體由相應奇異值大小決定，σi越小，則相應Si的信息量越小，Si的信息量可由下式綜合衡量[8]：

(6)

實際上，信息量過小的信號分量的意義不大，據此可以合理地確定矩陣行列。方法如下：取一系列不同的行數m構造Hankel矩陣，利用相應矩陣的奇異值計算各分量信號的信息量，并觀察它們的變化趨勢。若不論m取何值，從某一信息量ηi開始的后續信息量都趨于零，則表明第i個分量之后的其它分量并沒有多大意義，此時可以確定矩陣行數m=i，而列數為n=N-m+1。

1.3 相關峭度

峭度指標能有效地反映機械設備中的沖擊信號，峭度越大，沖擊越強。所以，很多學者利用峭度來提取滾動軸承由故障引起的沖擊信號[9]。但機械設備中沖擊源較多，如齒輪點蝕、滾動軸承表面損傷、泵中滾體氣蝕等。因此，僅用峭度來提取(或衡量)滾動軸承故障信號，有時有效性顯得不足。相關峭度(Correlated Kurtosis)CK既保留了峭度的特性，也具有相關函數的特性，它能提取一些特定周期的沖擊信號。相關峭度的計算公式為[5]：

(7)

式中，xn為信號序列，N為采樣長度，T為感興趣脈沖信號的周期，M為偏移的周期個數。

相關峭度是反映振動信號中特定周期脈沖信號強度的參數，它與脈沖信號的周期相關。相關峭度能夠準確反映出信號中故障沖擊信號的強度，因此特別適用于軸承表面損傷類故障。應用于滾動軸承時，給定偏移故障周期T，如果軸承存在故障，則與軸承故障周期相同的沖擊信號相關峭度較大，而其它沖擊信號的相關峭度很小。并且，相關峭度值越大，說明信號中故障沖擊信號所占的比重越多。所以，利用相關峭度能更加有效地提取故障信號。

1.4 基于SVD和相關峭度的特征提取方法

如上所述，當分量信號的相關峭度比較大時，可以判斷此分量的沖擊成分最為明顯，包含的軸承故障信息較多。利用SVD進行滾動軸承故障特征提取時，可以將相關峭度作為SVD分量的選擇依據。基于SVD和相關峭度的特征提取方法可以總結為以下幾個步驟：

(1)根據信號構造Hankel矩陣，對行數m取不同值時SVD分量信號的信息量變化趨勢進行分析，確定合理的矩陣結構。

(2)由確定的行列數構造出矩陣，通過SVD將原始信號分解為一系列分量信號的簡單線性疊加。

(3)求出每個SVD分量信號的相關峭度值，選取相關峭度值最大的分量，從而實現對原信號中故障特征的提取。

(4)對提取信號進行平方包絡解調分析，從而獲得信號的包絡譜，根據包絡譜中特征頻率對滾動軸承故障類型進行判斷。

2 仿真研究

為了驗證基于SVD和相關峭度的滾動軸承故障診斷方法的正確性和有效性，首先利用滾動軸承內圈故障的仿真信號進行研究分析。

2.1 信號仿真

滾動軸承發生早期故障時，測得的振動信號中既有弱故障信號，還包含齒輪嚙合、軸不對中等產生的諧波信號以及其它背景噪聲，可得滾動軸承內圈單個損傷點引起的振動模型如下[10]:

(8)

式中，Ai為以1/fr為周期的幅值調制，fr為軸的轉頻；B(t)為背景諧波分量，fm為齒輪嚙合頻率；s(t)為指數衰減脈沖，兩相鄰沖擊的間隔為T，τi為滑移引起的第i個脈沖的周期延遲；n(t)為白噪聲；A0、B0、CA為常數，CA>A0；R為由系統決定的衰減系數，fn為系統的自然頻率。

2.2 驗證與分析

設采樣頻率fs為16 384 Hz，轉頻fr為52 Hz，故障頻率fi為180 Hz，信號時長0.5 s。由(8)式可得仿真信號波形如圖1(a)所示，圖中顯示了局部放大后的一段時域波形，時域波形圖中包含明顯的諧波分量，故障信號微弱，再加上噪聲的干擾，很難看到故障沖擊。仿真信號的平方包絡譜分析結果如圖1(b)所示，可以看出解調診斷的效果欠佳，軸承轉頻譜線不明顯，故障特征頻率180 Hz雖能解調出來，但軸承內圈故障信號的調制特征沒有解調出來。由仿真信號的波形和平方包絡譜不能對故障進行有效診斷。

圖1 仿真信號

對長度N=8 192的仿真信號進行處理分析，先通過取一系列不同的行數m構造Hankel矩陣，利用相應矩陣的奇異值計算各分量信號的信息量，對分量信息量變化趨勢進行分析，可以確定矩陣行數m=20，列數n=8 173，然后進行SVD分解可得到20個分量信號。由感興趣分量周期T=1/fi，利用相關峭度公式(7)可得各分量的相關峭度值，峭度值曲線如圖2所示。由圖2可以看出，第4個分量信號的相關峭度值最大，進而對第4個分量信號進行提取。提取信號波形如圖3(a)所示，從其時域波形中能看到比較明顯的故障沖擊及幅值調制。對提取信號作平方包絡分析如圖3(b)所示，包絡譜圖能精確地指示故障特征頻率180 Hz及其各階倍頻分量，同時以各階倍頻為中心在其兩旁有間隔等于旋轉頻率的調制譜線。由平方包絡譜圖和軸承內圈故障信號的特征，能夠有效診斷出軸承內圈故障，這驗證了本文提出的基于SVD和相關峭度的滾動軸承故障特征提取方法的有效性。

圖2 相關峭度值曲線

3 實驗研究

3.1 實驗裝置

滾動軸承的實際振動信號來自實驗室的滾動軸承故障模擬平臺，實驗裝置如圖4(a)所示，故障軸承安裝在左端。實驗采用6 010型滾動軸承，滾動軸承的結構參數：軸承節徑D=65 mm，滾動體直徑d=9 mm，滾動體數目Z=13，接觸角為α=0°。該滾動軸承為內圈故障。實驗中使用加速度傳感器采集振動信號，測量點的布置如圖4(b)所示，傳感器采用鋼制螺栓固定，分別安放在軸承近端(測點1)和遠端(測點2)，并同時測量徑向和軸向的振動。

本文采用軸承遠端測得的軸向振動信號，軸承振動信號用B&K3560C振動噪聲分析系統測量獲得，采樣頻率為16 384 Hz。實驗轉速為2 022 r/min，即轉頻fr為33.70 Hz，由軸承幾何參數及各特征頻率與轉頻的關系[8]，可得內圈特征頻率fi=249.38 Hz。

圖4 滾動軸承模擬實驗臺

3.2 實驗數據及分析

實測振動信號的波形如圖5(a)所示，軸承故障信號從軸承到遠端測點，經傳遞過程產生衰減，加上機體振動、皮帶輪不平衡產生的振動等背景噪聲，可以看到皮帶輪處產生的明顯周期沖擊，而故障周期沖擊脈沖不明顯。實測振動信號的平方包絡譜如圖5(b)所示，可以看到由于背景噪聲的干擾，解調診斷的效果欠佳，只有34 Hz處近似轉頻譜線清晰可見，故障特征頻率250 Hz雖能解調出來，但軸承內圈故障信號的調制特征沒有解調出來。由實測信號的波形和平方包絡譜，無法對軸承故障進行有效判斷。

取實測信號的8 192個數據點進行處理分析，通過取一系列不同的行數m構造Hankel矩陣，利用相應矩陣的奇異值計算各分量信號的信息量，對分量信息量變化趨勢進行分析，可以確定矩陣行數m=50，列數n=8 143，然后進行SVD分解得到50個分量信號。構造Hankel矩陣，根據經驗對信號進行SVD分解得到50個分量。由感興趣分量周期T=1/fi，利用相關峭度公式(7)可得各分量的相關峭度值，相關峭度值曲線如圖6所示。由圖6可以看出，第12個分量信號的相關峭度值最大，進而對第12個分量信號進行提取。提取信號的波形如圖7(a)所示，圖中可以看出明顯的故障沖擊及轉頻的幅值調制。對提取信號進行平方包絡分析得到的包絡譜如圖7(b)所示，圖中可以看到內圈故障特征頻率250 Hz(理論計算值249.38 Hz)及其倍頻，且譜線較為明顯。包絡譜中也可看到轉頻34 Hz(理論計算值33.70 Hz)，以及圍繞內圈通過頻率及其諧波、間距為轉頻的調制邊帶。根據軸承內圈故障轉頻調制特點，由平方包絡譜結果能夠診斷軸承故障為內圈故障。

通過對實測信號運用基于SVD和相關峭度的滾動軸承故障特征提取方法，有效提取了軸承弱故障信號，通過進一步的包絡分析，準確地對軸承故障的類型和位置作出了判斷，證明了該診斷方法是有其優越性的。

圖5 實測信號

圖7 提取信號

4 結 論

本文在分析了SVD的信號分解原理和周期脈沖信號相關峭度定義的基礎上，提出了結合SVD信號分解和相關峭度的滾動軸承弱故障特征提取方法，即首先通過SVD對信號進行分解，然后通過選擇相關峭度最大的分量信號，提取出軸承弱故障信號。利用該方法對軸承內圈故障仿真信號進行處理，驗證了該方法的有效性。為了檢驗它的實際效果，本文將此方法應用到實測信號中進行了檢驗，結果表明：該方法能夠有效提取軸承弱故障信號，對于軸承故障的監測和故障診斷是可行的。

[1]周智，張優云，朱永生，等．基于MMSE和譜峭度的滾動軸承故障診斷方法[J]．振動與沖擊，2013，32(6)：73-77．

ZHOU Zhi, ZHANG You-yun, ZHU Yong-sheng, et al. Fault diagnosis method for rolling bearings based on MMSE and spectral kurtosis[J]. Journal of Vibration and Shock, 2013, 32(6): 73-77.

[2]趙學智，葉邦彥，陳統堅．基于小波-奇異值分解差分譜的弱故障特征提取方法[J]．機械工程學報，2012，48(7)：37-48．

ZHAO Xue-zhi, YE Bang-yan, CHEN Tong-jian. Extraction method of faint fault feature based on wavelet-SVD difference spectrum[J]. Journal of Mechanical Engineering, 2012,48(7): 37-48.

[3]趙學智，陳統堅，葉邦彥．基于奇異值分解的銑削力信號處理與銑床狀態信息分離[J]．機械工程學報，2007，43(6)：169-174．

ZHAO Xue-zhi, CHEN Tong-jian, YE Bang-yan. Processing of milling force signal and isolation of state information of milling machine based on singular value decomposition [J]. Journal of Mechanical Engineering, 2007,43(6)：169-174．

[4]趙學智，葉邦彥，陳統堅．基于SVD的奇異性信號檢測原理及其應用[J]．振動與沖擊，2008，27 (6)：11-14．

ZHAO Xue-zhi, YE Bang-yan, CHEN Tong-jian. Piezoelecric shunt damping for vibration control of a precisemens system [J]. Journal of Vibration and Shock. 2008，27 (6)：11-14．

[5]McDonald G L，Zhao Q，Zuo M J．Maximum correlated kurtosis deconvolution and application on gear tooth chip fault detection[J]．Machanical Systems and Signal Processing，2012，33：237-255．

[6]Golub G H，Van Loan C F．袁亞湘，譯．矩陣計算[M]．北京：科學出版社，2001．

[7]Akitas A G，Malaschonok G I．Application of singular value decomposition (SVD) [J]．Mathematics and Computers in Simulation，2004，67(1)：15-31．

[8]趙學智，葉邦彥，陳統堅．矩陣構造對奇異值分解信號處理效果的影響[J]．華南理工大學學報(自然科學版)，2008，36 (9)：86-93．

ZHAO Xue-zhi, YE Bang-yan, CHEN Tong-jian. Influence of matrix creation way on signal processing effect of singular value decomposition [J]. Journal of South China University of Technology(Natural Science Edition) . 2008, 36 (9): 86-93.

[9]胡愛軍，馬萬里，唐貴基．基于集成經驗模態分解和峭度準則的滾動軸承故障特征提取方法[J]．中國電機工程學報，2012，32 (11)：106-111．

HU Ai-jun, MA Wan-li, TANG Gui-ji. Rolling bearing fault feature extraction method based on ensemble empirical mode decomposition and kurtosis criterion [J]. Proceedings of the CSEE. 2012, 32 (11): 106-111.

[10]MING Yang，CHEN Jin，DONG Guang-ming．Weak fault feature extraction of rolling bearing based on cyclic Wiener filter and envelope spectrum [J]．Machanical Systems and Signal Processing, 2011, 25(5): 1773-1785.