隨機失諧周期壓電Timoshenko 梁的波動局部化研究

丁 蘭，尹 濤，朱宏平

(1.華中科技大學 土木工程與力學學院，武漢 430074;2.武漢大學 土木建筑工程學院，武漢 430072)

智能材料和結構在使用過程中能夠感知外界環境的變化，并能針對這種變化做出適當的反應。因其具有自感應和主動控制的能力，所以被廣泛應用于各種工程領域。在各種智能材料中，壓電材料在今后的智能結構振動控制研究和工程應用中占有極其重要的地位，特別是壓電周期結構得到了越來越廣泛的應用［1］。周期結構具有通頻和禁頻等特殊的力學性質，而失諧周期結構還會表現出振動及波的局部化特性［2］。局部化導致波動幅值沿失諧周期結構以空間指數形式衰減，利用此性質即可有效控制結構振動在特定頻率范圍內的傳播。

由于力電耦合效應的影響，壓電周期結構將呈現一些新的物理性質，對其進行的研究也會變得復雜。以往的研究多局限在純彈性周期結構方面，近年來一些學者開始著手研究周期壓電結構中的振動波傳播及局部化問題。Baz等［2］對周期壓電質量－彈簧系統的振動主動控制進行了研究;Li等［3］研究了層狀周期壓電復合材料結構中的波動局部化問題，并利用Lyapunov指數方法給出了結構中局部化因子的表達式。Wang等［4］研究了Rayleigh表面波在隨機失諧壓電聲子晶體中的傳播，得出了一些有意義的結論。上述研究對象都是針對周期性地嵌有壓電材料的結構，而就目前的研究現狀來看，對其它類型的周期壓電智能結構的相關研究，僅有為數不多的報道，如 Thorp等［1，5］分別針對周期壓電貼片桿結構中的振動波傳播與局部化以及板結構的振動主動控制等問題進行了研究。顯然，對此種表面粘貼壓電片的周期結構的波傳播及其局部化問題的研究尚不夠深入，有待更進一步地開展。自從Lin等［6］首次利用傳遞矩陣方法研究了波在加固板結構中的傳播特性，大部分學者直接求解結構的運動方程得到傳遞矩陣，對于大型復雜結構運動方程的求解相對困難，而 Solaroli等［7－8］則采用有限單元方法得到周期加固殼和疊合梁結構的傳遞矩陣，為本文分析周期性地粘貼壓電片的Timoshenko梁結構提供了參考。

本文基于Timoshenko梁理論，考慮基梁和壓電片的轉動慣量和剪切效應，研究了軸－彎耦合隨機失諧壓電Timoshenko梁中的波動局部化問題。采用有限單元法和傳遞矩陣法相結合，提取了結構的動剛度矩陣，推導了結構相鄰胞元間的傳遞矩陣，并給出了局部化因子的表達式，進而分析了幾何尺寸和材料特性失諧對周期壓電結構波動局部化的影響，對失諧壓電周期結構振動控制研究提供了理論參考。

1 軸－彎耦合壓電Timoshenko梁的傳遞矩陣

圖1所示為一周期性粘貼壓電片的彈性梁。設壓電周期結構中含有n個胞元，每個胞元中含有兩個子結構，分別稱為子結構1和子結構2。為使問題簡化，假設壓電層和基梁完好聯結無滑移，且具有相同的橫向位移w1(x，t)和轉角ψ1(x，t)，其中下標1代表子結構1。

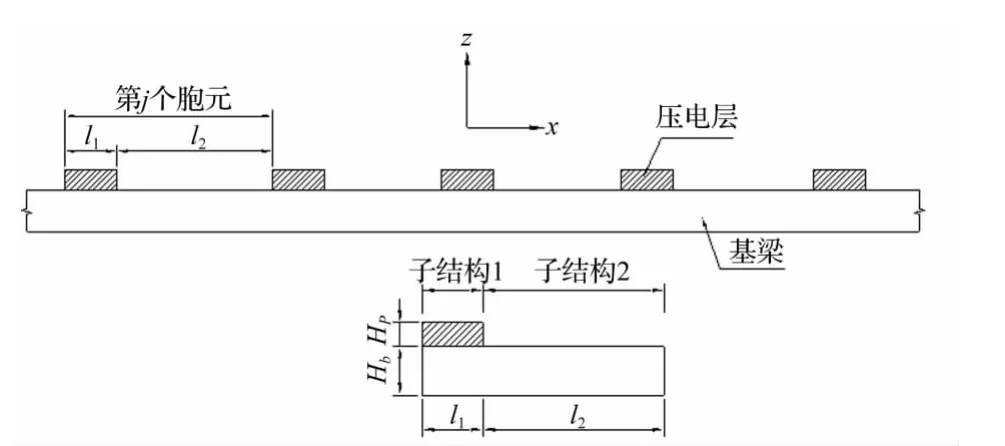
圖1 周期壓電梁的結構簡圖Fig.1 Schematic diagram of the periodic piezoelectric beam

將每層均作為Timoshenko梁考慮，彈性－壓電雙層梁(子結構1)的變形見圖2。

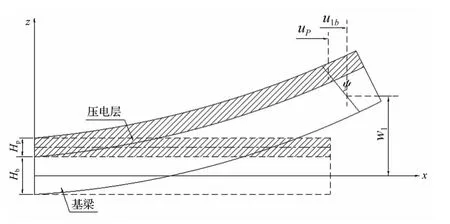
圖2 彈性－壓電雙層梁的變形示意圖Fig.2 Deformation of the elastic-piezoelectric two-layer beam

對于界面層完好聯結的情況，

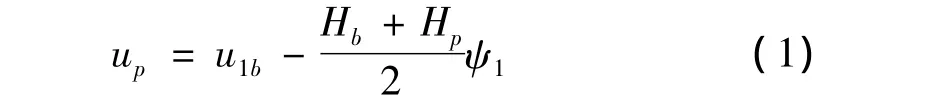
式中，u1b、up、Hb和Hp分別為基梁和壓電層的軸向位移和厚度;下標b和p分別表示基梁層和壓電層。

壓電材料在軸向荷載作用下的本構方程為［9］

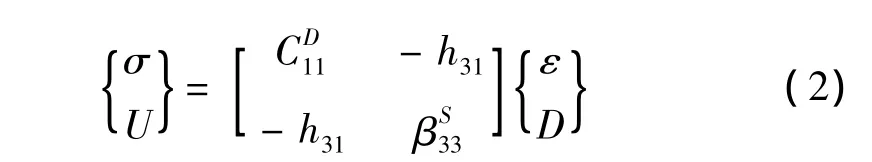
式中，σ和ε分別為x方向的應力和應變;D和U分別為電位移和電場強度;CD11、βS33和h31分別為彈性剛度、介電常數和壓電常數。

在閉路狀態下，運用方程(2)中的本構關系，子結構1的勢能V1和動能T1可表示為

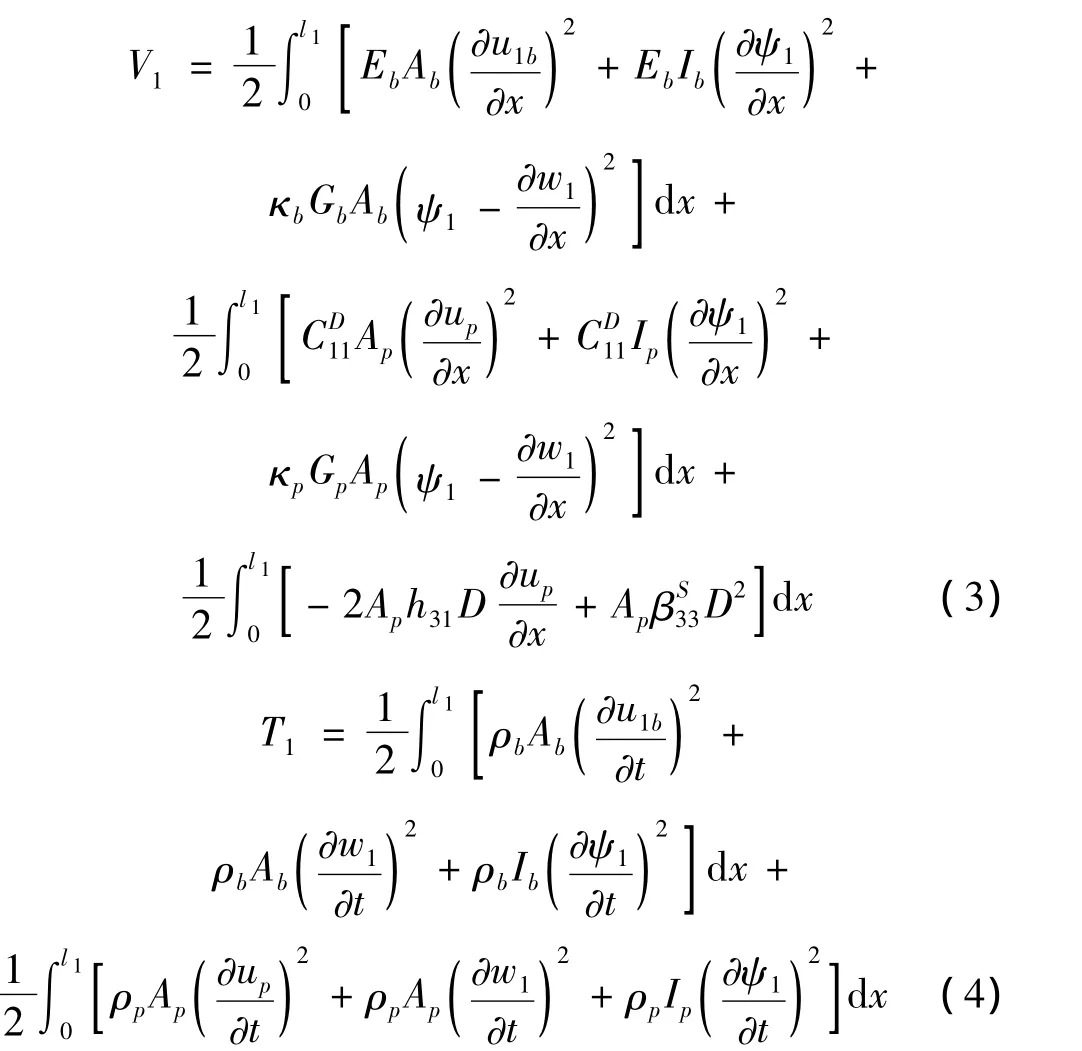
其中，E、G、A、I、κ 和 ρ分別為壓電層和基梁的楊氏模量、剪切模量、橫截面面積、慣性矩、橫截面抗剪形狀系數和密度。

子結構2的勢能V2和動能T2可分別表達為

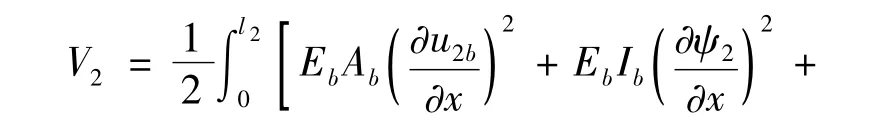
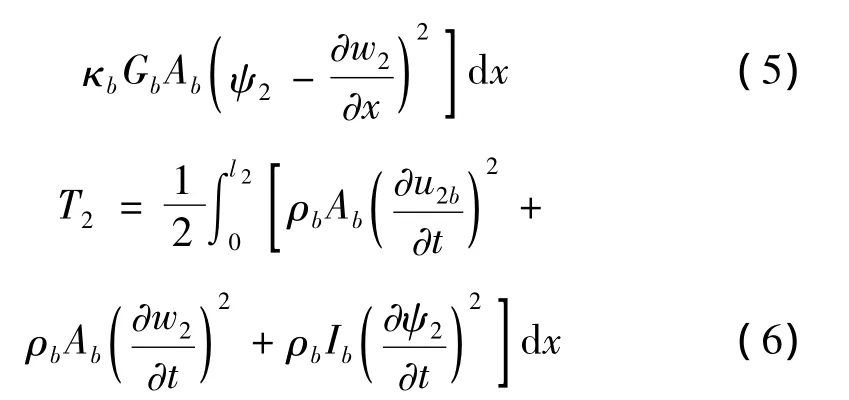
其中，u2b、ψ2和w2分別為子結構2的軸向位移、轉角和橫向位移。

將各子結構的運動表示為位移自由度和形函數的級數:

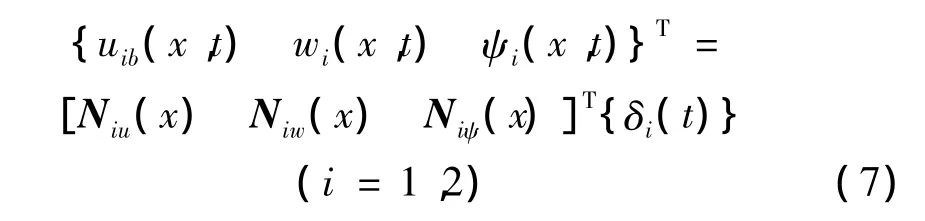
式中，i代表子結構編號。形函數 Niu(x)、Niw(x)、Niψ(x)分別表示為［10］

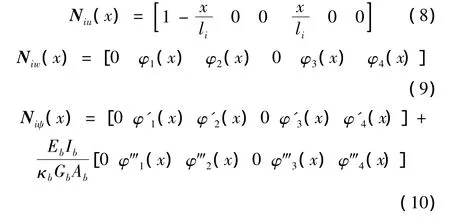
式中

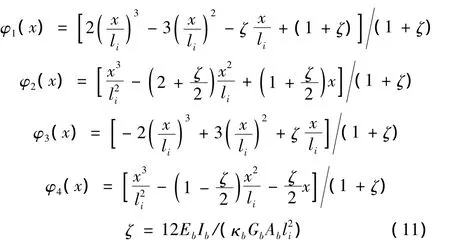
節點自由度向量為

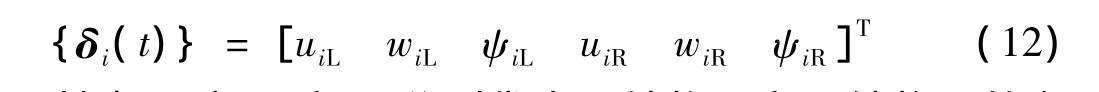
其中，下標L和R分別代表子結構1和子結構2的左右節點。

將式(7)代入式(3)和(4)，并利用式(1)消除up，可得子結構1的勢能和動能

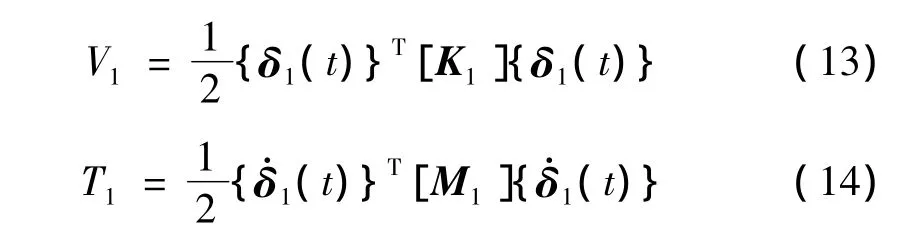
同理，將式(7)代入式(5)和(6)可得子結構2的勢能和動能

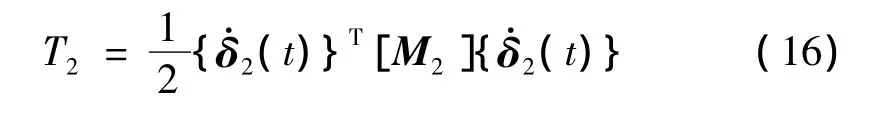
式中，［K1］、［K2］、［M1］和［M2］分別為子結構 1 和子結構2的剛度矩陣和質量矩陣:

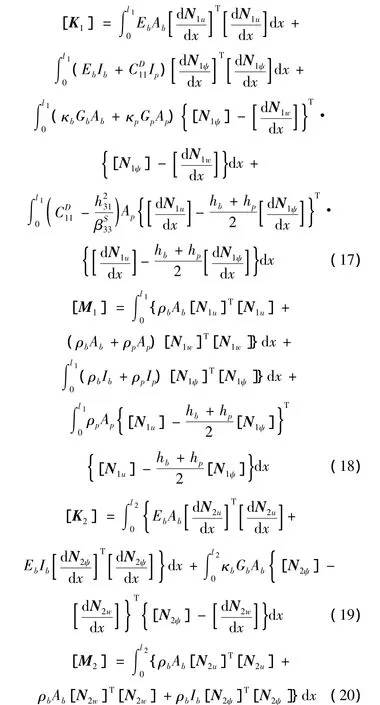
當周期結構以頻率ω振動時，利用上式(17)－(20)可得子結構1和子結構2的動剛度矩陣

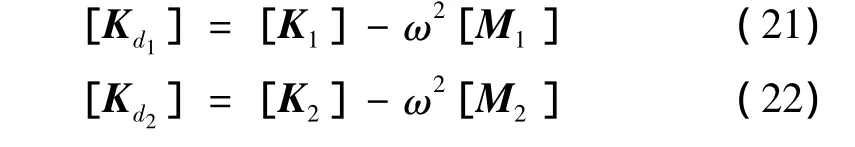
根據動剛度矩陣，第j個胞元中各個子結構的動態運動方程可表示為

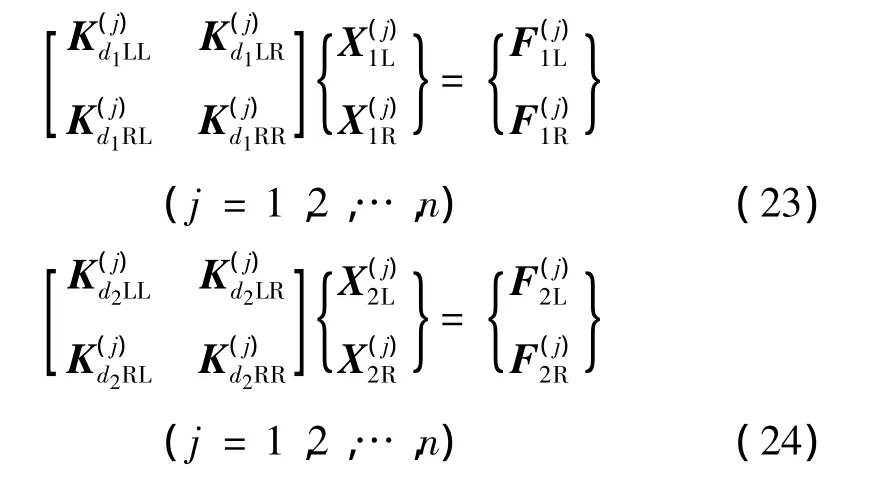
經調整，式(23)和(24)可表達為

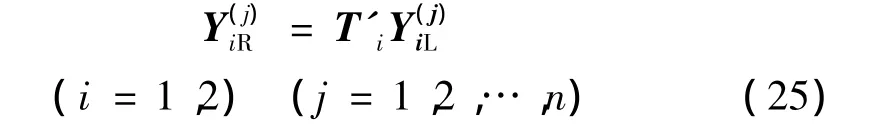
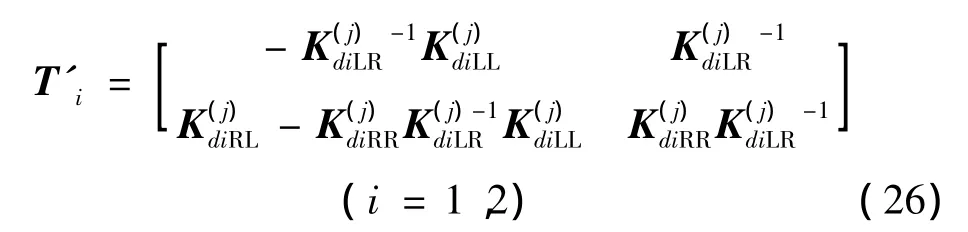
兩個子結構界面處滿足

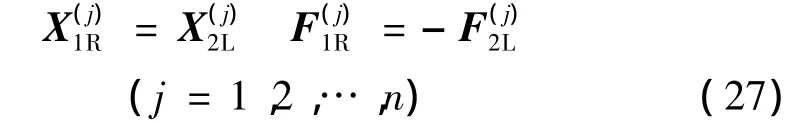
式(27)可以表示為如下矩陣形式

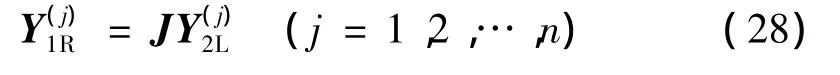
其中，

I為3階單位矩陣。

利用式(25)和(28)，得到第j個胞元左右兩端狀態向量間的關系式為

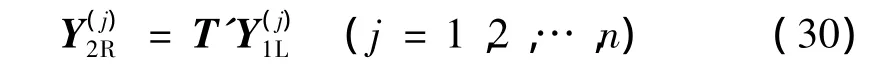
式中T'=T'2J－1T'1為第j個胞元中的傳遞矩陣。

第(j－1)個胞元右端和第j個胞元左端界面處滿足

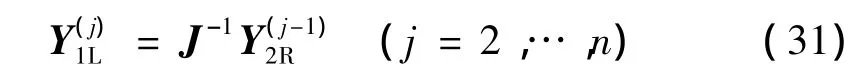
代入(30)得第(j－1)個胞元和第j個胞元狀態向量間的關系式為

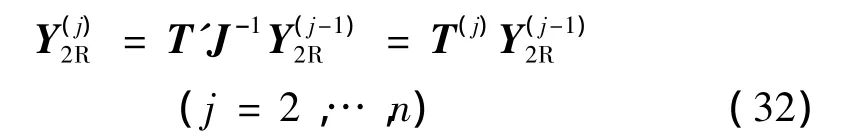
由上式可見，T(j)=T'J－1=T'2J－1T'1J－1即為兩相鄰胞元間的傳遞矩陣。

2 波動局部化

Lyapunov指數是對相空間中相鄰相軌線的平均指數發散程度或收斂程度的度量，它定性地和定量地對動力系統的力學行為進行了有力的描述［11］。研究周期結構中彈性波的傳播和局部化時，引用Lyapunov指數的概念，可以提供一種關于彈性波幅值衰減程度的度量指標。局部化導致波動幅值沿失諧周期結構漸近地以空間指數形式衰減，而相應的波動幅值的空間指數衰減常數稱為局部化因子。因此，局部化因子用來表示彈性波沿周期結構傳播時，波動幅值的空間指數衰減程度［11］。

根據周期結構的對稱性，可以證明，Lyapunov指數總是以互為相反數的關系成對出現。若結構傳遞矩陣的階數2d×2d，(d＞1)，則可將Lyapunov指數按從大到小的順序排列為

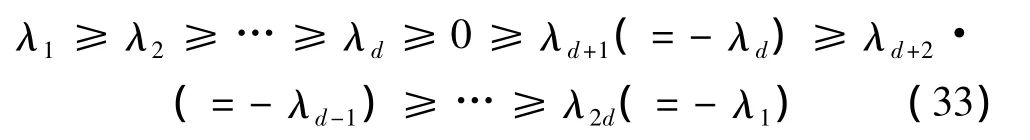
Lyapunov指數中的最小正值λd代表了幅值衰減程度最小的波，它在結構中傳播的距離最遠，沿結構傳輸的能量也最遠，刻畫了系統中彈性波和振動的主要衰減特性。因此，最小正的Lyapunov指數定義為局部化因子［3－4］。

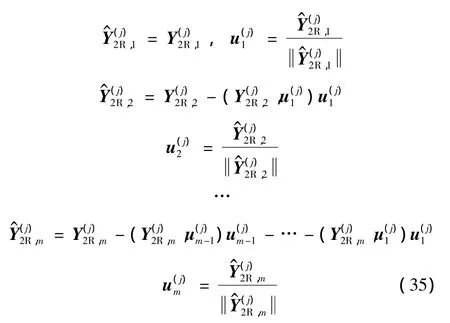
Wolf［12］給出了計算連續型動力系統中 Lyapunov指數的方法，借鑒此方法，可以給出離散型系統中Lyapunov指數的計算方法。對于傳遞矩陣階數為2d×2d的結構，為了計算第m(1≤m≤2d)個Lyapunov指數，需選擇m個正交的2d階初始單位狀態向量u(0)1，u(0)2，…，u(0)m，利用式(32)可計算出每次迭代的狀態向量。對于第j次迭代

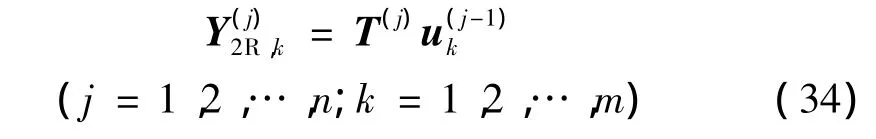
根據Wolf算法，第m(1≤m≤2d)個Lyapunov指數的表達式為:

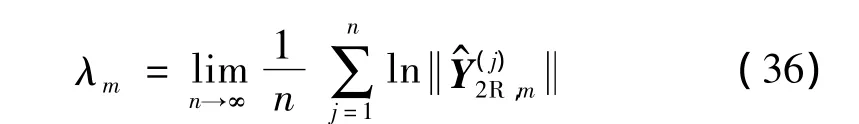
式中n為周期結構的胞元數。

利用式(36)，可以計算出 d對互為相反的 Lyapunov指數，第d個Lyapunov指數λd即為局部化因子。對于本文中的諧和周期結構，相鄰胞元間的傳遞矩陣T(j)保持不變，且其維數為6×6，因此局部化因子為λ3。利用局部化因子即可分析失諧周期結構的波動局部化現象。

3 算例及分析討論

根據上述理論模型，本文考慮不同結構尺寸和材料參數失諧對結構局部化的影響。其中，基梁彈性材料采用鋁和鋼兩種，壓電材料采用 PKI 502［9，13］，子結構的長度l2=5l1=0.5 m，所用到的材料參數如表1所示。計算過程中取無量綱頻率作為自變量。

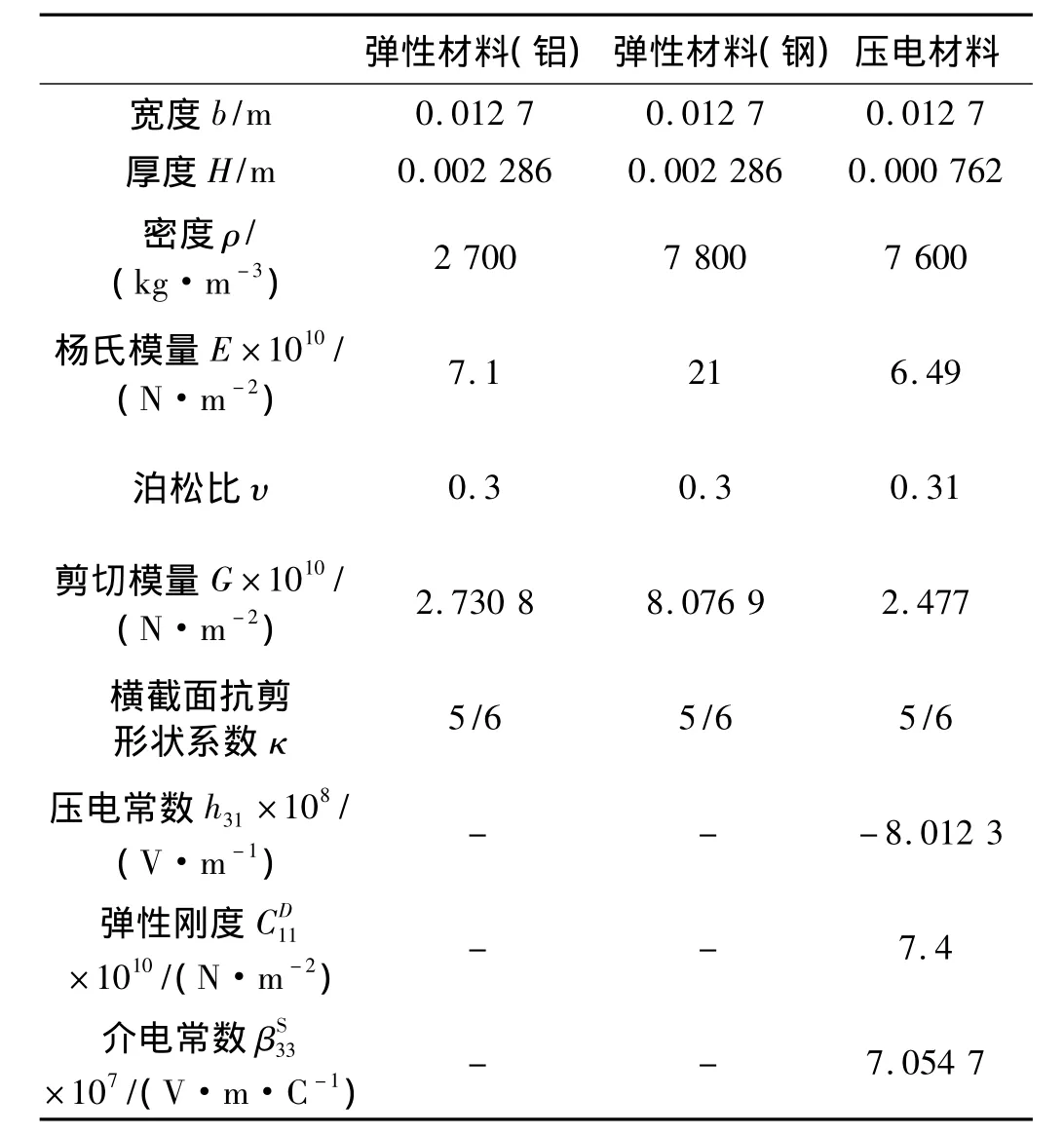
表1 基梁和壓電層的材料常數表Tab.1 Material properties of the base beam and piezoelectric layer

3.1 長度l2失諧

基梁彈性材料為鋁，考慮子結構2的長度l2失諧，設其服從均值為l'2=0.5 m，變異系數為δ的均勻分布，則 l2的取值范圍可表示為［3－4］

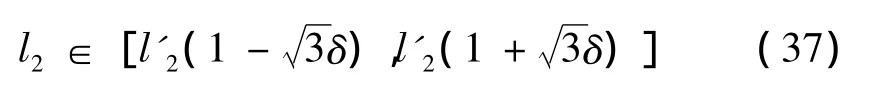
引入一服從標準均勻分布的隨機變量η∈(0，1)，則l2可表示為

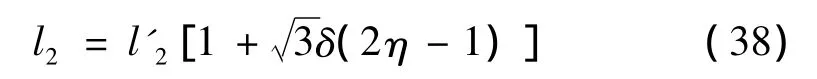
圖3給出了長度l2失諧，變異系數δ取不同值時，局部化因子隨無量綱頻率的變化曲線。

由圖3可觀察到，當變異系數δ=0時，諧調周期結構存在明顯的頻率通帶和禁帶，在無量綱頻率區間Ω∈(0，71.5)內，局部化因子 λ3=0，該區間即為頻率通帶;在頻率范圍 Ω∈(71.5，145.7)內，局部化因子λ3＞0，該區間即為頻率禁帶。當變異系數δ＞0時，對應δ=0為頻率通帶的邊界區間，局部化因子也大于零，出現波動局部化現象，表明失諧周期結構在特定頻率范圍內能控制波在結構中的傳播。隨著變異系數的增加，禁帶的寬度和局部化因子的幅值逐漸增加，該區間的局部化程度相應地增強。因此可以設計不同的變異系數來微調結構的頻帶區間和局部化程度。

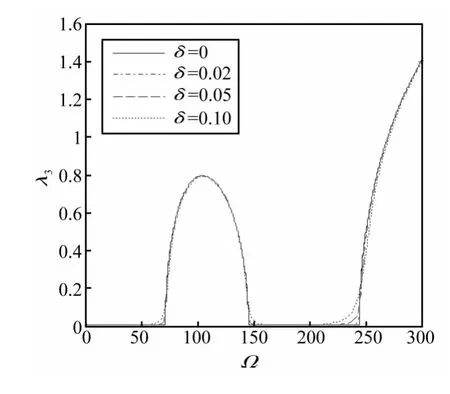
圖3 長度失諧下局部化因子隨無量綱頻率的變化Fig.3 Localization factors versus dimensionless frequencies for disordered length of the purely elastic beam

3.2 壓電材料彈性剛度失諧

基梁彈性材料分別為鋁和鋼，考慮壓電材料的彈性剛度失諧，即，此時，彈性剛度均值仍取，分析變異系數不同時壓電材料的彈性剛度失諧對周期結構波動局部化的影響，計算結果見圖4。

由圖4可知，不同的基梁彈性材料對周期壓電結構頻帶特性影響顯著，盡管曲線形狀類似，但在第一個禁帶區間，鋼梁的禁帶帶寬和局部化因子幅值都小于鋁梁，表明在此頻率范圍內，波動在鋁梁中的衰減程度更大。因此，可以根據實際需要選擇不同的基梁彈性材料，以達到對結構進行有效的振動控制。比較圖4中的四個子圖可以發現，周期壓電結構的局部化行為對壓電材料彈性剛度失諧不夠敏感，在特定頻率范圍內，彈性波不僅可以在諧調周期結構中傳播，也可在失諧周期結構中傳播。這種現象可能是由于壓電材料為壓電陶瓷材料，其彈性模量和密度等參數都較大，在此周期結構中占彈性剛度較大的組分，因此其變化對結構的局部化影響很小，可以通過調整基梁及壓電材料的彈性剛度比以使得振動控制效應顯著。

3.3 壓電參數對波動局部化的影響

基梁彈性材料為鋁，當長度l2失諧且其變異系數δ=0.10，壓電材料的壓電參數變化，即壓電常數h31及介電常數βS33分別選取不同值時，局部化因子隨頻率的變化曲線如圖5所示。

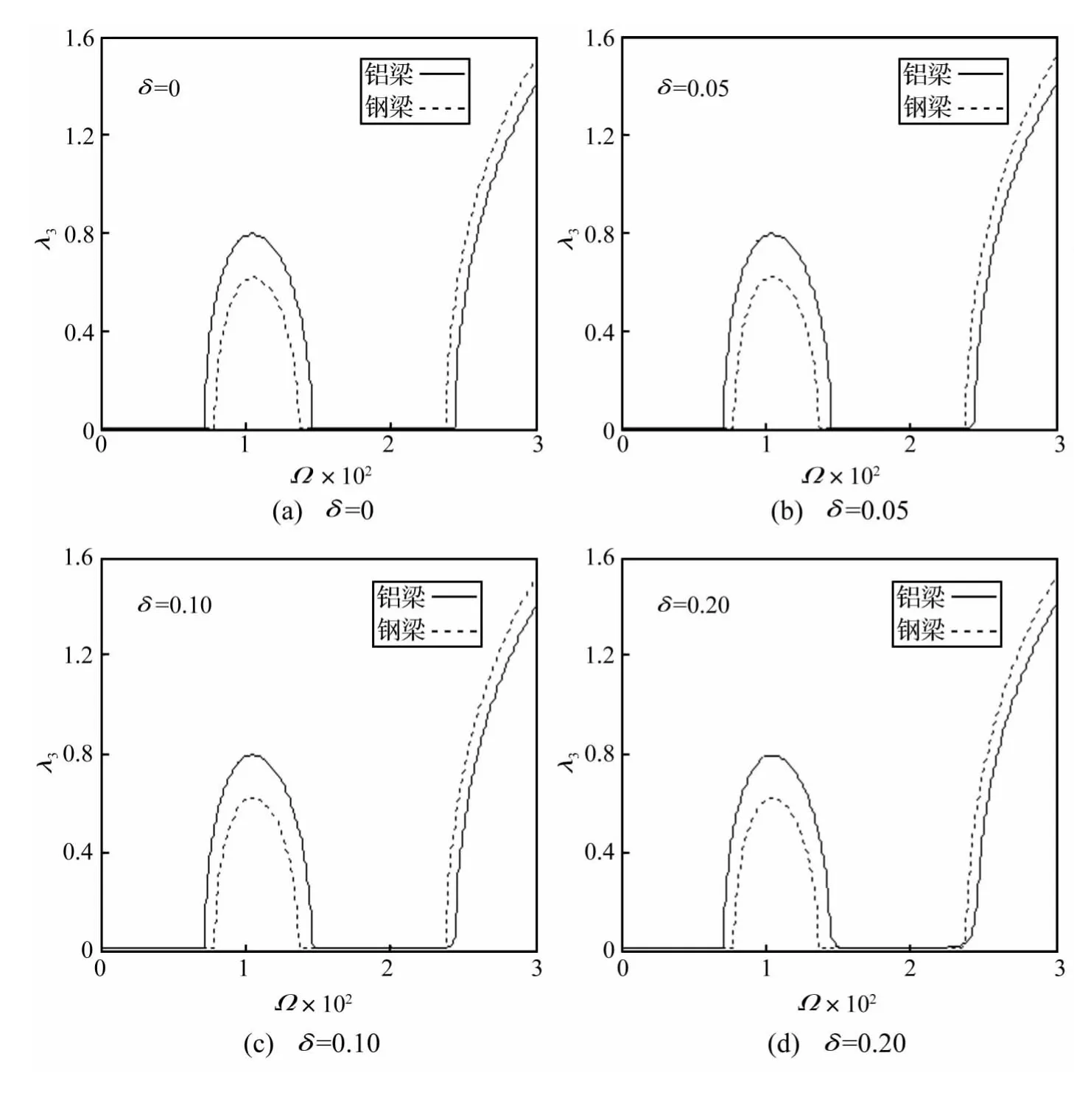
圖4 壓電材料彈性剛度失諧下局部化因子隨無量綱頻率的變化Fig.4 Localization factors)versus dimensionless frequenciesfor disordered elastic stiffness of piezoelectric material

圖5 壓電參數變化下局部化因子隨無量綱頻率的變化Fig.5 Effects of different piezoelectric parameters on localization factors for disordered length of the purely elastic beam with δ=0.10

由圖5可見，對于同一失諧度，壓電參數對周期結構頻帶特性及局部化程度影響甚微，不同壓電常數和介電常數的結構在低頻區內，局部化因子曲線保持不變;在整個頻率范圍內，頻率通帶和禁帶帶寬幾乎相同。但隨著壓電常數增加，局部化因子的峰值在第一個禁帶降低，而在第二個禁帶則增加;介電常數的變化規律與其則剛剛相反。

4 結論

本文對隨機失諧周期壓電Timoshenko梁的波傳播及其局部化行為進行了研究。通過數值算例分析得到以下結論:對于本文周期壓電梁而言，基梁長度隨機失諧僅能輕微地改變結構的波動局部化特性;失諧度越大，波動局部化程度越強。不同基梁材料對結構的頻帶特性會有較明顯影響;而壓電材料參數變化，尤其是壓電材料彈性剛度隨機失諧對頻帶性質和局部化程度的影響則非常有限。因此，隨機失諧并不能顯著地改變本文周期壓電梁的波動特性。

［1］Thorp O，Ruzzene M，Baz A.Attenuation and localization of wave propagation in rods with periodic shunted piezoelectric patches［J］.Smart Materials and Structures，2001，10(5):979－989.

［2］Baz A.Active control of periodic structures［J］.ASME，Journal of Vibration and Acoustics，2001，123(4):472－479.

［3］Li F M，Wang Y S.Study on wave localization in disordered periodic layered piezoelectric composite structures ［J］.International Journal of Solids and Structures，2005，42(24－25):6457－ 6474.

［4］Wang Y Z，Li F M，Huang W H，et al.The propagation and localization of Rayleigh waves in disordered piezoelectric phononic crystals［J］.Journal of the Mechanics and Physics of Solids，2008，56(4):1578 －1590.

［5］Spadoni A，Ruzzene M，Cunefare K.Vibration and wave propagation control of plates with periodic arrays of shunted piezoelectric patches［J］.Journal of Intelligent Material Systems and Structures，2009，20(8):979 －990.

［6］Lin Y K，Mcdaniel T J.Dynamics of beam-type periodic structures［J］.Journal of Engineering for Industry，1969，91(4):1133－1141.

［7］Solaroli G，Gu Z，Baz A，et al.Wave propagation in periodic stiffened shells:spectralfinite elementmodeling and experiments［J］.Journal of Vibration Control，2003，9(9):1057－1081.

［8］Yeh J Y，Chen L W.Wave propagations of a periodic sandwich beam by FEM and the transfer matrix method ［J］.Composite Structures，2006，73(1):53 －60.

［9］Lee U，Kim J.Dynamics of elastic piezoelectric two-layer beams using spectral element method ［J］.International Journal of Solids and Structures，2000，37(32):4403－4417.

［10］諸葛榮，陳全公.框架振動的有限元分析－Timoshenko梁理論的應用［J］.上海海運學院學報，1982，3(4):9－24.ZHUGE Rong，CHEN Quan-gong.The finite element analysis for truss vibration-the application of Timoshenko beam theory［J］.Journal of Shanghai Maritime University，1982，3(4):9－24.

［11］陳阿麗，李鳳明，汪越勝.失諧壓電周期結構中波動的局部化［J］.振動工程學報，2005，18(3):272－275.CHEN A-li， LiFeng-ming， WangYue-sheng. Wave localization in disordered periodic piezoelectric structures［J］.Journal of Vibration Engineering，2005，18(3):272－275.

［12］Wolf A，Swift J B，Swinney H L，et al.Determining Lyapunov exponents from a time series［J］.Physica D，1985，16(3):285－317.

［13］Lee U，Kim J.Spectral element modeling for the beams treated with active constrained layer damping ［J］.International Journal of Solids and Structures，2001，38(32－33):5679－5702.