變速變槳距風力發電機組的智能控制

鄧文斌 王維慶 吐松江·卡日 饒成誠 吳 寒 孟 威

(1.新疆大學電氣工程學院，烏魯木齊 830047；2.國網湖南省電力公司超高壓管理局，長沙 410004；3.華潤電力控股有限公司宜昌分公司，湖北 宜昌 443000)

目前，風力發電機組的控制技術已經由定槳距控制發展到變速變槳控制，其關鍵環節是控制策略和控制器的設計。為了提高電網的電能質量、降低風能轉換系統所承受的載荷、最大限度地捕獲風能并延長設備壽命[1,2]，筆者提出將機組輸出功率的變化作為變槳距執行機構運行的判斷標準。由于風力發電機組是非線性、強耦合的系統[3]，對于一個復雜多變量的不確定系統，采用模糊控制可以有效地滿足其要求[4～6]，使其根據風速變化情況實現變速變槳運行。

1 變槳距控制理論①

風力發電機組主要由機械部分和電能轉化部分組成。風輪是機械部分能量轉換的關鍵部件，風以軸向風速流過風輪時捕獲的功率為：

Pr=0.5πρCp(β,λ)R2ν3

(1)

式中Cp(β,λ)——風能利用系數；

Pr——風輪吸收的功率；

R——風輪半徑；

ν——軸向風速，m/s；

ρ——空氣密度。

風能利用系數Cp表示風能利用率，與葉尖速比λ和槳距角β成非線性函數關系：

(2)

根據式(2)可以獲得風能利用系數的曲線，如圖1所示。

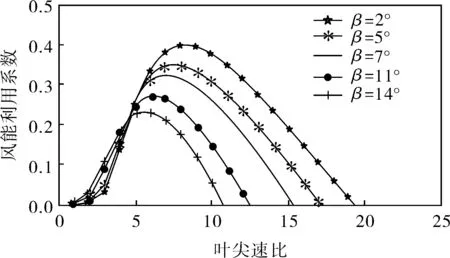
圖1 風能利用系數曲線

從圖1可知：

a. 對于某固定的槳距角β，存在唯一的最大風能利用系數Cpmax(β,λ)，且有最佳葉尖速比λopt；

b. 隨著槳距角β的增大，風能利用系數Cp(β,λ)減小。

風力發電機組的參數值由風速、電機轉速及發電機輸出功率等因素實現獨立控制，但由于風速的不確定性，一般通過電機的轉速來反饋控制槳距角的變化[7]，從而實現變槳距控制。

2 傳動系統模型

忽略傳動鏈的內部動態過程，將其簡化成單質量塊。作用于單質量塊傳動鏈，對于非直驅式風力發電機組，其傳動鏈運動方程為：

(3)

式中CT(β,λ)——風輪轉矩系數；

Jr——風輪轉動慣量；

Tm——齒輪箱轉矩；

Tr——風輪轉矩；

γ——齒輪箱的增速比；

ω——風輪轉速。

當齒輪箱的轉矩傳遞給發電機時，忽略發電機自身的系統阻力矩，其轉動慣量為：

(4)

式中Jd——異步發電機轉動慣量；

ωd——發電機轉速，ωd=ωγ。

將式(3)、(4)結合，可得到風電機組傳動系統方程：

(5)

3 控制系統設計

3.1 風電機組變速變槳控制策略

常規的風電機組變槳控制策略由風速大小而定。當風速低于額定風速時，風電機組可以視為定槳距運行；當風速高于額定風速時，此時實現變槳距運行以確保其安全穩定運行。

模糊控制屬于智能控制，且具有數學模型不依賴于被控對象、魯棒性好、抗干擾強及能克服非線性因素影響等優點，其可將專家的經驗和知識表示成語言規則而實現控制，適用于難以建立精確數學模型的對象。根據功率的變化情況，通過模糊控制適時調整變槳距執行機構的變槳速度，實現其變速運行，與常規PI的變槳控制方法相比，變速變槳方案可以抑制超速、超載的出現，減輕變槳距執行機構的疲勞度，降低其故障發生率，延長使用壽命[8～10]。

假設風電機組額定功率為Ps，輸出功率為P0，則功率誤差為ΔP=P0-Ps，誤差變化率為dΔP/dt。筆者研究瞬變風速在額定風速以上和額定風速以下的情況，風力機吸收的功率如圖2所示。根據功率變化，再結合變速變槳風電機組的模糊控制策略，可推知：

a. 若ΔP<0，并且輸出功率持續增大。當功率誤差變化率增大時，變槳距執行機構減小槳距角，此過程減速變槳；當功率誤差變化率保持不變時，變槳距執行機構減小槳距角，此過程保持當前變槳速度；當功率誤差變化率減小時，變槳距執行機構減小槳距角，此過程加速變槳。

b. 若ΔP>0，并且輸出功率持續增大。當功率誤差變化率增大時，變槳距執行機構增大槳距角，此過程加速變槳；當功率誤差變化率保持不變時，變槳距執行機構增大槳距角，此過程保持當前變槳速度；當功率誤差變化率減小時，變槳距執行機構增大槳距角，此過程減速變槳。

c. 若在Ps處(即ΔP=0)變槳距執行機構不運行，保持當前槳距角不變。

d. 若ΔP>0，并且輸出功率持續減小。當功率誤差變化率增大時，變槳距執行機構增大槳距角，此過程加速變槳；當功率誤差變化率保持不變時，變槳距執行機構增大槳距角，此過程保持當前變槳速度；當功率誤差變化率減小時，變槳距執行機構增大槳距角，此過程減速變槳。

e. 若ΔP<0，并且輸出功率持續減小。當功率誤差變化率增大時，變槳距執行機構減小槳距角，此過程減速變槳；當功率誤差變化率保持不變時，變槳距執行機構減小槳距角，此過程保持當前變槳速度；當功率誤差變化率減小時，變槳距執行機構減小槳距角，此過程加速變槳。

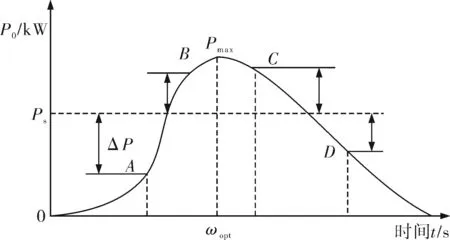
圖2 風力機的吸收功率

由于傳統的PI控制器屬于反饋控制器，僅當偏差存在時，控制才起作用，并且在當時的風速下，整定好的PI參數合適，可能隨著風速的變化其效果不一定理想。在此控制策略中，采用了模糊控制系統，無需根據實時測量的風速建立精確數學模型，只需通過功率變化情況、模糊控制器輸出及時調整變槳速度，即可使風力發電機組穩定輸出額定功率[11]。

3.2 模糊控制器的設計

模糊控制器非常適用于變速變槳風力發電機組這種非線性控制系統，因此筆者提出結合上述控制策略構建模糊控制器。系統控制結構如圖3所示。

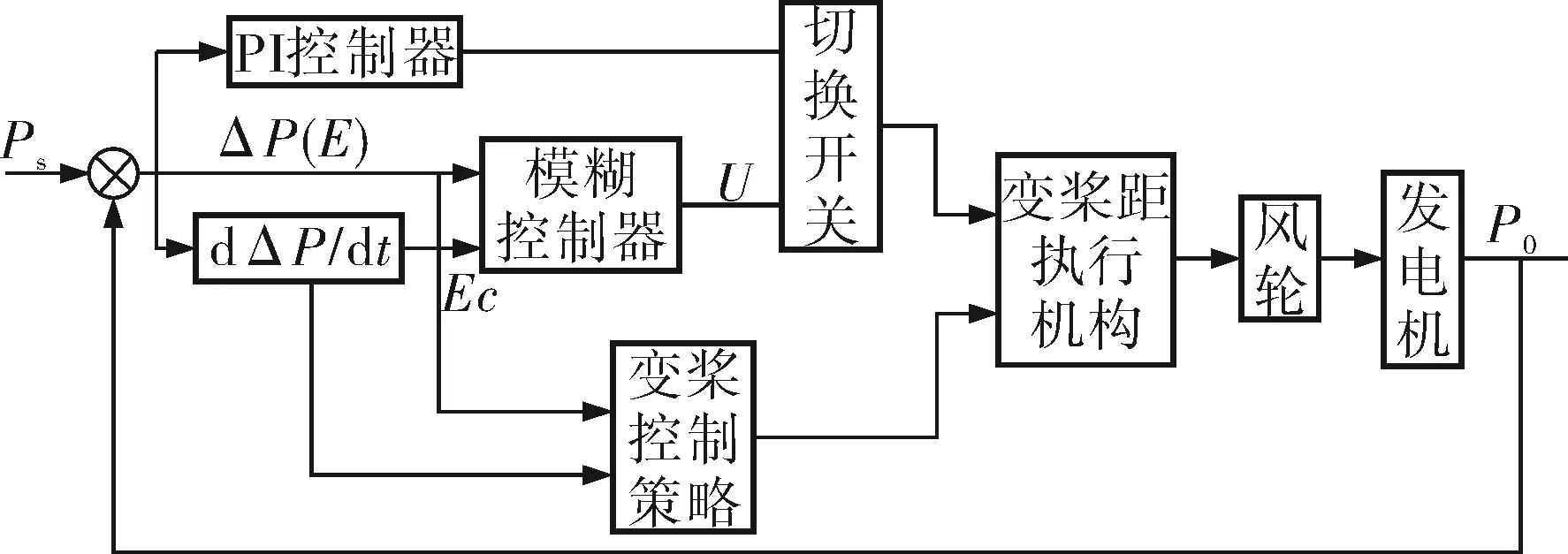
圖3 系統控制結構框圖

模糊控制的輸入變量為功率誤差E和誤差變化率Ec，輸出變量為變槳速度U。通過數據分析，結合專家經驗，可得功率誤差和誤差變化率的基本論域為[-1×105W，1×105W]，取輸出U的基本論域為[0°/s,5°/s]。輸入變量和輸出變量的量化因子與比例因子都是常數，合理地設計其值，使得控制器的輸入、輸出變量的基本論域分布在模糊論域[-6,6]，對應的模糊子集為{NB,NM,NS,ZO,PS,PM,PB}，分別用負大，負中，負小，零，正小，正中，正大表示。由此根據功率調節要求，結合經驗可制定模糊控制規則(表1)。

4 仿真結果

在Matlab/Simulink仿真中，研究模擬的風力發電機組一般參數：空氣密度ρ=1.25kg/m3，切入和切出風速分別為3m/s和25m/s，風輪和電機的轉動慣量Jr=2.5×106kg·m2、Jd=52kg·m2，齒輪箱的傳動比γ=79；額定功率為2MW，變槳距風力發電機組能夠在風速不斷變化中正常運行，發電機組模型如圖4所示。

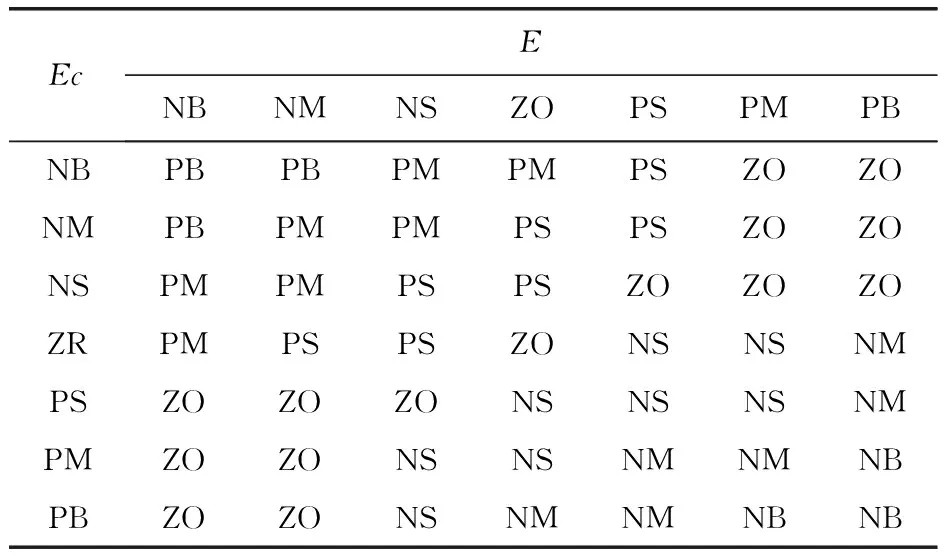
表1 模糊控制器規則

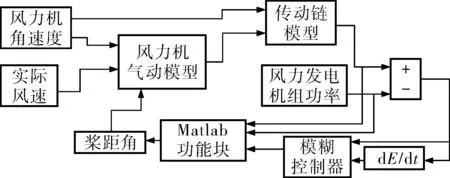
圖4 變速變槳風力發電機組模型

當風速變化曲線如圖5所示，仿真結果如圖6所示，其中圖6a為PI控制仿真結果,圖6b為模糊控制仿真結果。

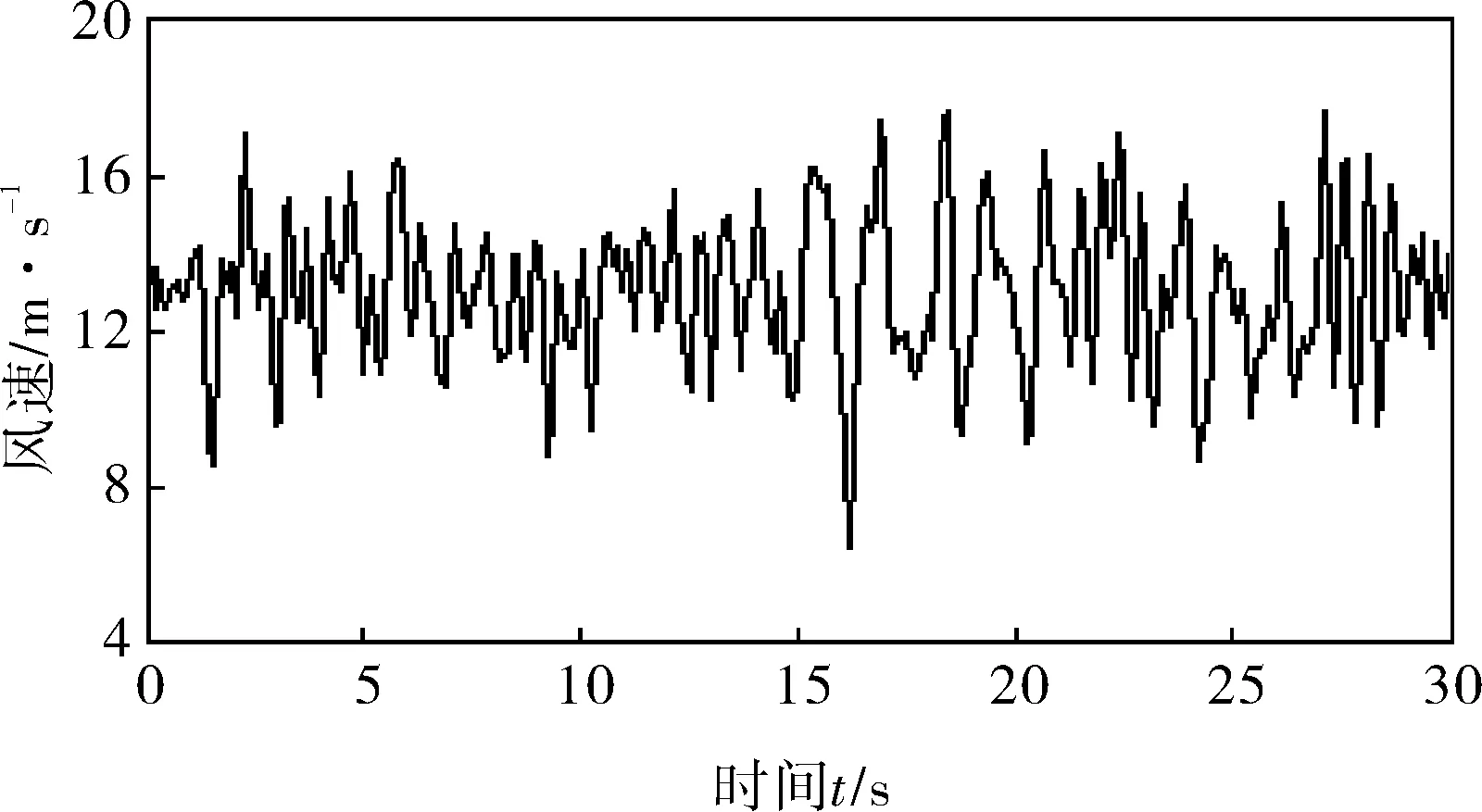
圖5 風速變化曲線

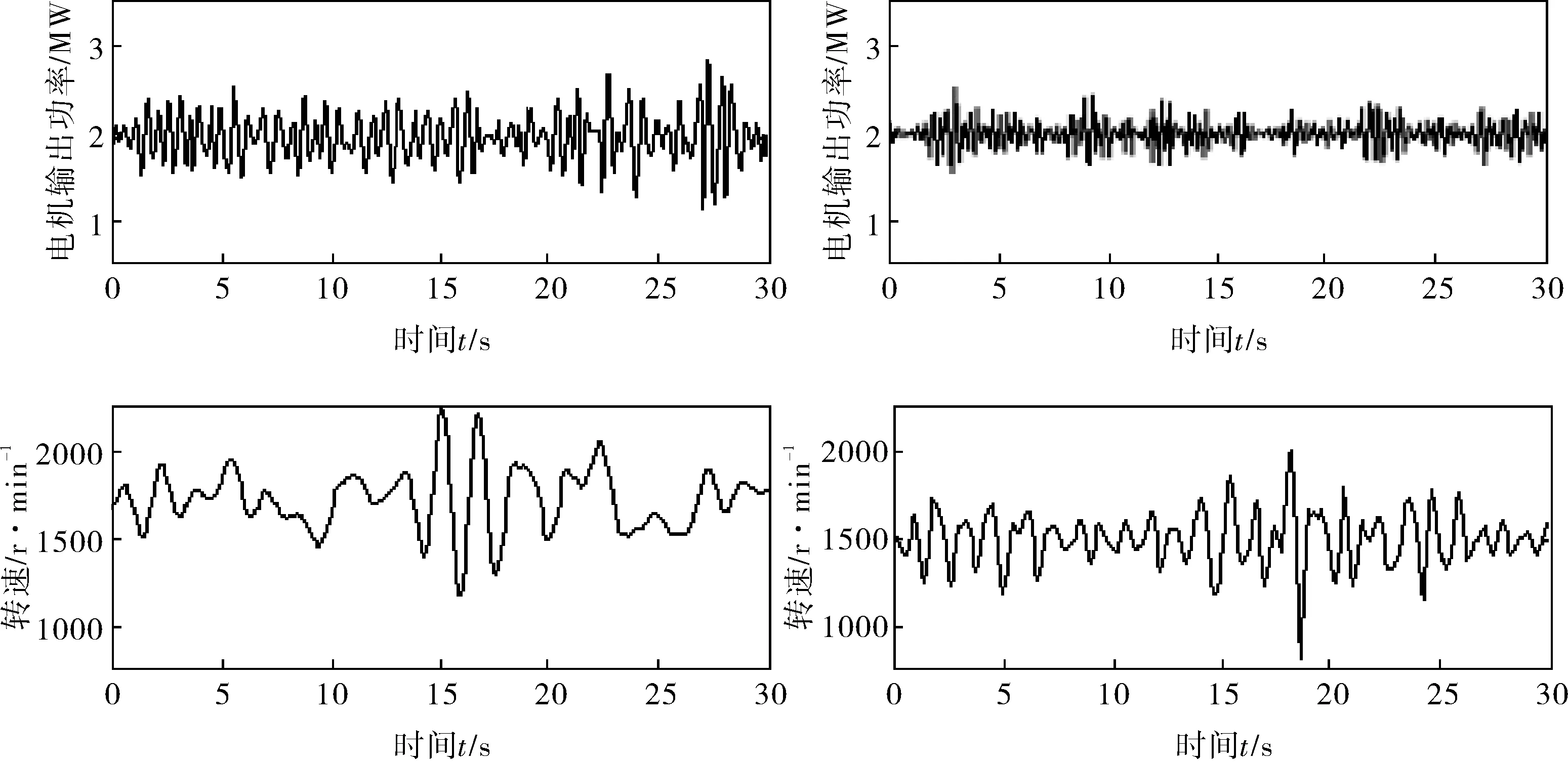
圖6 仿真結果

可見，模糊控制時，隨著風速不斷的變化，模糊控制器可以快速實現小范圍的槳距角調節，抑制系統功率輸出的波動，從而降低電磁轉矩的振動。但由于風力機慣性比較大，通過調節槳距角抑制功率波動需要一段響應時間。

通過仿真結果可得知，對比PI控制，筆者提出的基于功率變化作為變槳距控制策略的判斷依據[12]，槳距角變化速度快，變槳幅值區間小。若瞬態風速高于額定風速時，電機輸出功率幅值略高于額定功率，電機調節的轉速小，從而達到安全穩定的輸出功率。

5 結束語

筆者將模糊控制器引入變槳距控制系統中，結合一種基于功率變化判斷的控制策略，實現風力發電機組在風速不斷變化和瞬時變化的情況下迅速調節其輸出功率的變速變槳控制方法。通過對比傳統的PI控制器和模糊控制器的控制性能，可知所提模糊控制方法具有較強的魯棒性，不要求精確的數學模型，可廣泛應用于復雜的非線性系統。該模糊控制器彌補了傳統PI控制器難以在電機高速運轉和變槳距執行機構快速變槳的不足。