改進多智能體蟻群算法在電力系統無功優化中的應用

姚建紅 張玲玉 孫大興

(東北石油大學，黑龍江 大慶 163318)

電力系統無功優化在電能質量、網絡損耗和電壓穩定性上有著決定性的作用，但目前還沒有一種在計算時間、運算量及收斂性等方面兼具良好效果的優化算法。人工智能方法在電力系統無功優化上應用比較廣泛，但仍有不足之處，對于常規蟻群算法而言主要體現在[1]：沒有堅實的數學基礎，也沒有成型的系統分析方法，計算復雜[2]，易陷入局部最優及收斂速度慢[3]等。對于常規蟻群算法的缺陷，筆者利用多智能體系統與改進的蟻群算法相結合，優勢互補，克服了易陷入局部最優解和收斂速度受限的不足，從而實現較快、較精準的無功優化。

1 無功優化的數學模型①

無功優化的數學模型由目標函數、約束條件構成，其中約束條件包括等式約束條件和不等式約束條件。

以配電網電能損耗最小為目標函數：

(1)

選取潮流方程作為等式約束條件：

(2)

式中Bij、Gij——分別表示系統節點導納矩陣中第i行第j列元素的虛部、實部；

gij——支路i-j電導；

n——系統總支路數；

Pi、Qi——分別為節點i的有功、無功功率；

Ui、Uj——節點i、j的電壓幅值；

δi、δj——節點i、j的相角；

δij——節點i、j的相角差。

選取發電機無功出力、無功補償裝置的無功補償容量和有載調壓變壓器的變比作控制變量，負荷節點電壓作狀態變量。控制變量不等式約束條件為：

(3)

狀態變量不等式約束條件：

Uimin≤Ui≤Uimax

(4)

式中QCi——第i個無功補償裝置的無功補償容量；

QCimax——第i個無功補償裝置的無功補償容量上限；

QCimin——第i個無功補償裝置的無功補償容量下限；

QGi——節點i發電機無功出力；

QGimax——節點i發電機無功出力上限；

QGimin——節點i發電機無功出力下限；

Ti——第i臺有載調壓變壓器變比；

Timax——第i臺有載調壓變壓器變比可調節的上限；

Timin——第i臺有載調壓變壓器變比可調節的下限；

Ui——節點i的電壓幅值；

Uimax——節點i電壓幅值的上限；

Uimin——節點i電壓幅值的下限。

2 多智能體蟻群算法

2.1 改進的蟻群算法

在數學領域中的旅行商問題中，有學者將遺傳算法中的排序概念擴展到蟻群算法中[4]，改進后的算法得到了較好的收斂速度。進而，在此基礎上對蟻群算法的權系數改進，并應用在電力系統無功優化領域中，以解決收斂速度慢等問題。

改進蟻群算法的思想：把螞蟻尋優的一次循環結束后生成的路徑按照長短排序，每只螞蟻對更新信息素的貢獻取決于生成路徑的長短，路徑越短貢獻越大。改進權系數λk(1-N/Nmax)，對于全局信息素更新來說，所有螞蟻都有相應的貢獻。不僅在尋優過程中，提高對較優螞蟻的重視程度，也降低對較差螞蟻的忽略程度。因此，該算法是一種較好的改進算法。

在改進的算法中，搜索路徑上的信息素按照下式對全局信息素更新：

τij(t+1)=ρ×τij(t)+Δτij

(5)

(6)

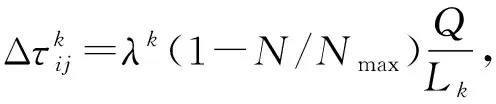
式中k——最優螞蟻編號；

Lk——第k只最優螞蟻搜索的路徑長度；

λ——常數(0<λ<1)；

N——當前迭代次數；

Nmax——最大迭代次數；

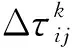
對改進蟻群算法與一般蟻群算法進行驗證，在初始參數設置相同的前提下，對比結果如圖1表示。

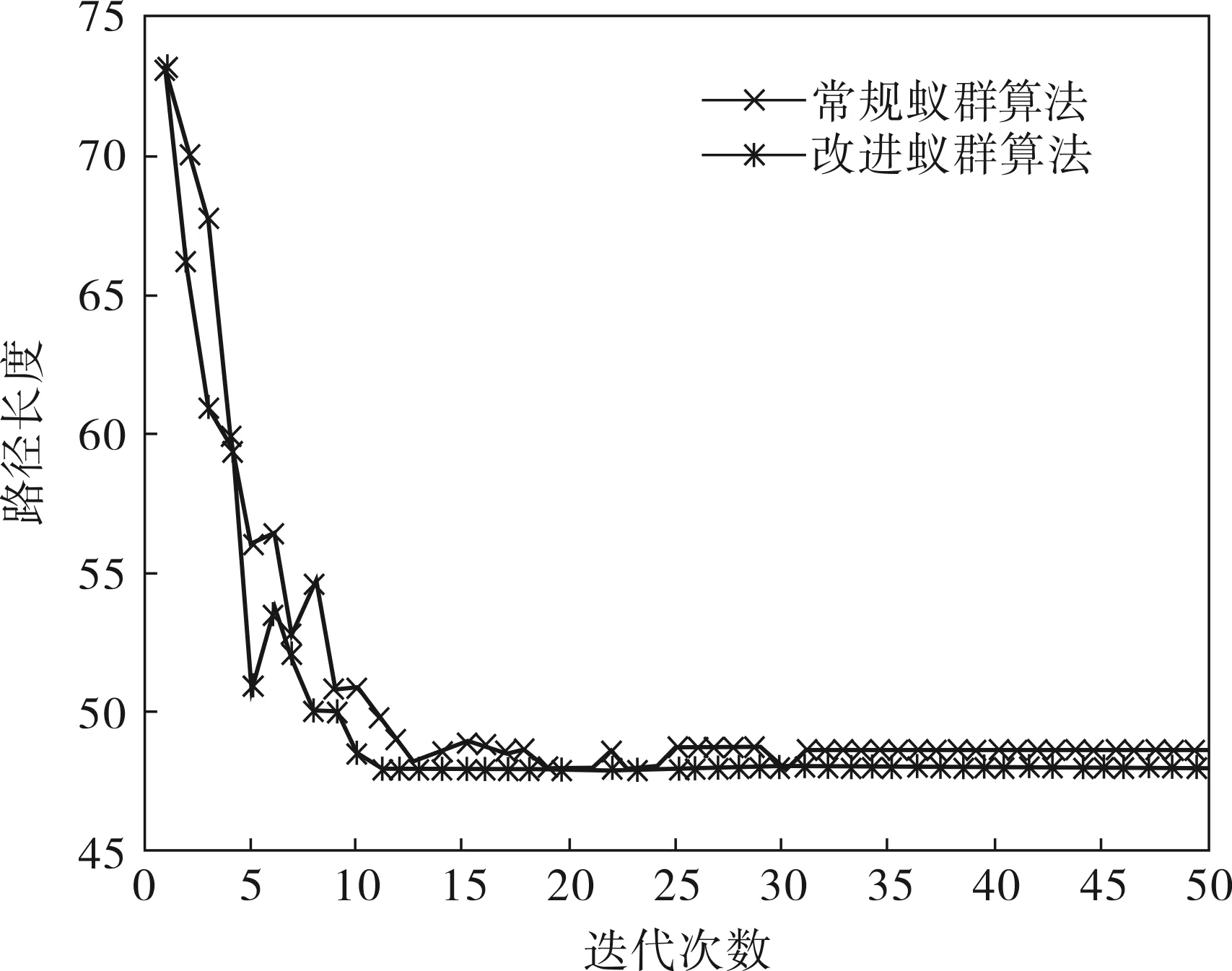
圖1 改進蟻群算法與常規蟻群算法對比

由圖1可知：改進蟻群算法和常規蟻群算法分別在迭代11次左右和13次左右得到全局最優解；改進的蟻群算法在搜索全局最優解收斂的過程較平穩，而常規蟻群算法在31代收斂，卻陷入局部最優解。由此可知，基于排序加權的蟻群算法，在收斂速度上有明顯的提高，有較好的實用性。

2.2 多智能體蟻群算法

多智能體系統，即Multi-Agent System，簡稱MAS，多個智能體(Agent)相互協作可以完成更復雜問題的求解，MAS將各種不同功能的Agent模塊通過通信和協作結合起來，共同協調來完成任務，具有更大的靈活性和適應性[5]。

多智能體蟻群算法(Multi-Agent Ant Colony Optimization，簡稱MACO)是將改進的ACO和MAS的主要特征結合的一種優化算法。該改進的算法主要思想是任意一個Agent相當于改進蟻群算法中種群的一只螞蟻，都有一個被優化問題決定的最佳適應值。Agent的目的就是在滿足運行條件的限制下，盡可能減小其適應值。每個Agent不但可以和其鄰居競爭與合作操作、自學習操作，還結合蟻群的搜索機制，與全局最優的智能體進行信息共享，并根據自身經驗總結來修正智能體的行動策略，能夠更快、更準確的收斂到全局最優解。

2.3 MACO算法的優化步驟

筆者改進算法的具體優化步驟如下：

a. 設置初始參數、約束條件的上/下限值、算法中需指定的控制參數和最大迭代次數；

b. 創建MAS中Agent“生存”的“格子”環境，產生初始的Agent，初始迭代次數為0；

c. 利用牛頓拉弗遜方法進行潮流計算，對每個Agent的適應值進行評估；

d. 每個Agent與其鄰居競爭與合作，操作完成后，更新一次整個環境中的Agent；

e. 在MAS中，執行排序加權蟻群算法，進一步更新每個Agent在解空間的位置；

f. 重新對Agent的適應值進行評估；

g. 搜索最優適應值的Agent，再根據Agent的自學習操作，對Agent在解空間的位置再一次更新；

h. 迭代次數自加1；

i. 判斷是否達到終止條件，即最大迭代次數或者滿足收斂條件，若不滿足，跳轉到步驟c，若滿足，則迭代終止，輸出優化的最優解。

3 算例分析

將改進的算法應用于IEEE30節點系統進行算例分析，驗證算法的有效性和可行性。系統中基準功率SB=100MVA，有6臺發電機，38條支路，4臺變壓器，9臺并聯電容器和21個負荷節點，系統總負荷Ptotal=2.834，Qtotal=1.262。系統中參數設置見表1、2。

表1 發電機參數

表2 變壓器變比參數

在初始條件下，通過潮流計算，得到ΣPG=2.869 1，ΣQG=1.380 7，網損Ploss約為0.035。初始參數為：總環境大小S=10(種群規模ant=100)，最大迭代次數Nmax=50，信息素啟發因子α=1，自啟發因子β=2，揮發系數ρ=0.1，加權系數λ=0.3，自學習環境大小s=4，自學習搜索半徑sR=0.4；運行后，與遺傳算法進行比較，表3顯示出在條件相同的前提下，優化算法的對比結果。

表3 優化結果對比表

由表3可得到：多智能體蟻群算法對電網系統優化后，網絡損耗為0.017，與遺傳算法相比，網損下降率增加了約17%，并且計算時間略短；對平衡節點進行潮流計算，無功功率比優化前大幅度降低，綜合經濟條件及優化結果等方面充分顯示出算法的有效性。

4 結論

4.1深入研究蟻群算法，對蟻群算法的信息素加權改進，驗證算法的可行性，比常規蟻群算法在收斂速度上具有一定的優勢。

4.2針對優化過程中易出現陷入局部最優解、搜索速度慢的情況，采用多智能體系統與改進蟻群算法的結合，經過實驗對比驗證，可以較快的達到搜索到全局最優解，即降低網損。

4.3利用遺傳算法與多智能體蟻群算法進行對比，筆者的算法有在運算速度和優化結果上均有較好的優勢。