基于云模型的獨立變槳距控制仿真研究

岳有軍 徐 玥 趙 輝，2 王紅君

(1.天津市復雜系統控制理論及應用重點實驗室，天津300384；2.天津農學院，天津300384)

獨立變槳距控制是在統一變槳距的基礎上發展起來的一種新型控制方法，根據3個槳葉各自的受力情況單獨進行調整，達到更好的控制效果。由于風切效應、塔影效應對風電機組的影響，風輪平面內風速的分布不均勻，因此在統一變槳距控制的基礎上設計基于槳葉方位角權系數的獨立變槳距控制系統。

在變槳距控制器的設計中，根據文獻[1～3]，模糊PID控制效果較好。風電機組有強非線性、時變不確定性的特點，而不確定現象和事物具有模糊性和隨機性。模糊PID控制是模糊控制與PID控制的結合，模糊控制需要用確定精確的隸屬度函數描述模糊集，使模糊的概念變得精確，在推理過程中失去模糊性，從而歸入精確數學理論中。但模糊控制只考慮了其模糊性，未能考慮風速變化導致的隨機誤差，因此用精確的函數來描述隸屬度函數是不客觀的。由于既要著重模糊性，也要考慮隨機性，因此筆者提出基于云模型的控制方法。

1 獨立變槳距控制系統①

1.1 風能利用系數

根據空氣動力學原理，風能利用系數會限制風電機組的實際功率，其計算式為：

(1)

式中CP——風能利用系數；

S——風輪旋轉一周所掃過的面積，m2；

ν——風速，m/s；

ρ——空氣密度，kg/m3。

根據風機葉片的空氣特性，風能利用系數是葉尖速比λ和槳距角β的函數[4]，CP=CP(λ，β)，即：

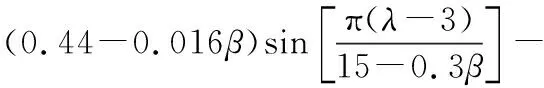
0.0018(λ-3)β

(2)

(3)

式中n——風輪轉速，rad/s；

R——風輪半徑，m；

ωr——風輪轉動角速度，rad/s。

通過軟件Matlab/Simulink可得到如圖1所示的風力機風能利用系數CP(λ，β)的函數曲線。風速在額定風速以上時，控制槳距角β，減小風能利用系數，保證穩定的功率輸出。

1.2 風輪迎風平面內風速特性分析

影響風速變化的原因有很多，除了風輪的布局、體形等因素外，高度的變化對風速也有著顯著的影響[5]。地面垂直高度增加，風速也隨之增加，只有高于300m時風速才不會受這些因素影響。風速在垂直高度的變化主要受風切效應和塔影效應影響[6]。

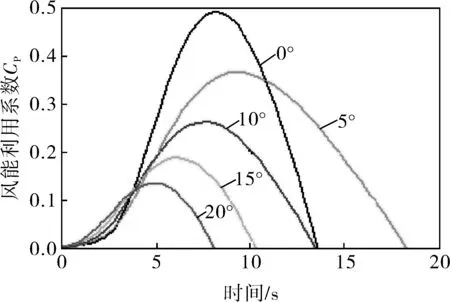
圖1 風力機風能利用系數CP(λ,β)的特性曲線

風剪切是穩定狀態下平均風速隨著高度的變化而變化。假設地面為零風速平面，則有風切公式為：

(4)

式中n——風剪切系數，它取決于大氣和地面的客觀因素，一般情況下取0.1～0.4；

νH——距地面H高度處的風速；

νH0——距地面H0高度處的風速。

在塔架的上游和下游，塔架對氣流的阻塞使風流速度減少，稱為塔影效應。對于上風向風力發電機，在塔影坐標系下某點上垂直于風力機風輪旋轉面的風速可以表示為：

(5)

式中ht——塔架在某點的塔架高度；

Rt——塔架半徑；

xt，yt——塔架坐標系下的水平兩個方向坐標；

Y——塔徑修正因子。

在風力機風輪旋轉平面內，如果該點的槳葉方位角沿中心相對于輪轂中心在之間，則式(5)成立。

1.3 基于槳葉方位角權系數分配的獨立變槳距控制

設計基于槳葉方位角權系數分配的獨立變槳距控制系統，在統一變槳距基礎上進行風力機各個槳葉槳距角的獨立調節，減少由風切效應和塔影效應引起的風力機槳葉的不均勻載荷，使輸出功率穩定輸出，延長風力機的使用時間。

風輪旋轉平面內的風速分布是不均勻的，高度對風速的影響最為顯著，風速在垂直高度上的變化主要是由風切和塔影效應導致的，可以根據槳葉所處風輪旋轉平面的位置來確定吹向槳葉的風速大小[7]。設水平面軸線為x軸，槳葉的旋轉方向以逆時針方向為正，槳葉的中心線與x軸之間的夾角θ定義為槳葉的方位角，可以通過槳葉的方位角來確定槳葉的具體位置。選定一個槳葉作為基準葉片，槳葉1的方位角θ作為起始方位角，則槳葉2的方位角為θ+120°，槳葉3的方位角為θ+240°。根據規定每個槳葉所受的平均風速是槳葉的中心位置，其平均風速為：

(6)

式中i——第i個槳葉，i=1,2,3；

ν——傳感器所測風速；

νi——每個槳葉所受平均風速；

θ——槳葉1的方位角。

基于槳葉方位角權系數分配的獨立變槳距控制的思路(圖2)：當風速高于額定風速時，首先運用變槳距控制器進行統一變槳距控制，得到風力機3個葉片統一變槳距的槳距角；然后根據槳葉方位角得到權系數重新分配每個槳葉的槳距角，實現獨立變槳距控制。

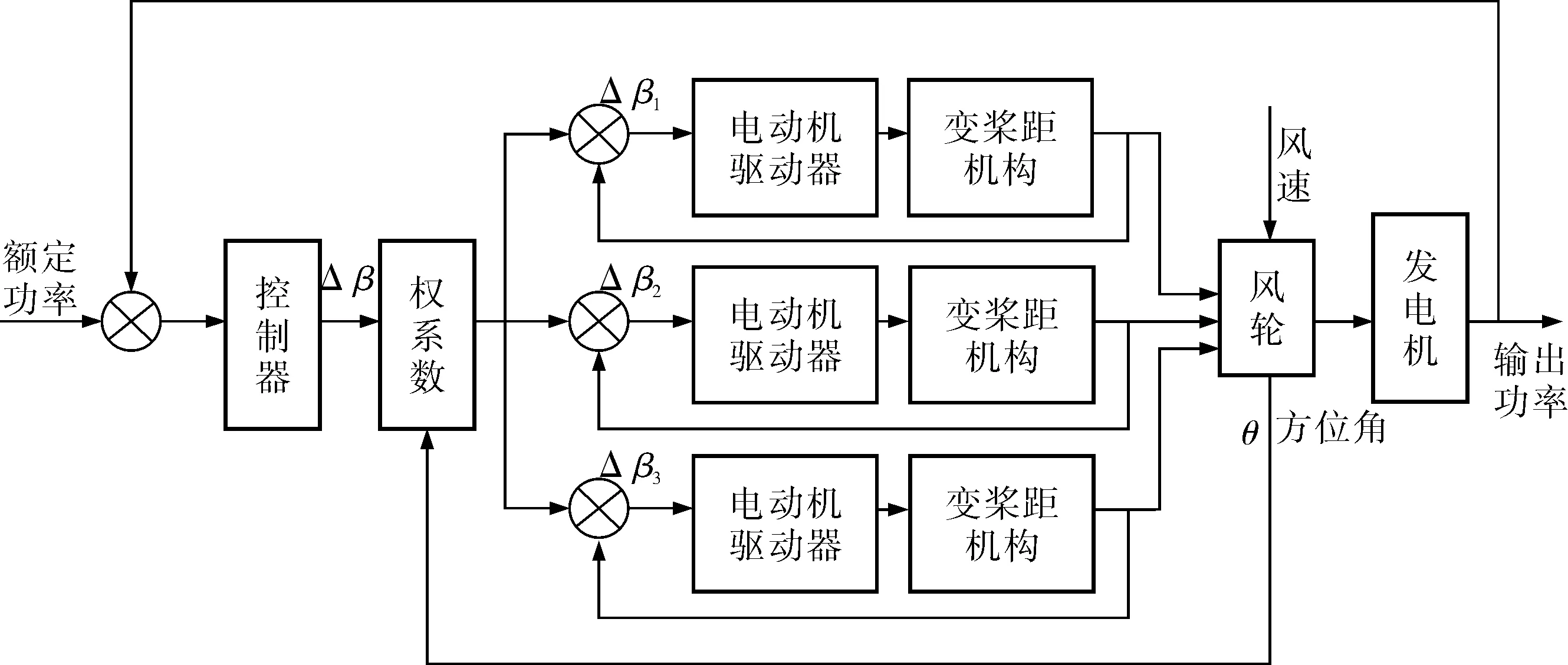
圖2 獨立變槳距控制系統

權系數是根據風力機每個槳葉的受風情況來分配的。權系數隨風速的變大而變大，槳距角隨權系數的增大而增大。其分配過程是根據每個槳葉的方位角θi設權系數Ki(i=1,2,3)，通過權系數將3個槳葉統一變化的槳距角Δβ進行分配，轉化為每個槳葉獨自變化的槳距角Δβi。

(7)

槳葉方位角權系數Ki的計算式為：

(8)

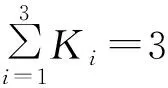
2 變槳距控制器的設計

2.1 模糊PID控制器的不足

在控制策略的研究中，模糊PID控制的控制效果比傳統PID控制及模糊控制等的控制效果好。模糊PID控制是模糊控制與常規PID控制算法相結合的一種新型控制方法，找出PID 3個參數與誤差、誤差變化率之間的模糊關系，建立模糊規則，在運行中不斷檢測誤差和誤差變化率，根據確定的模糊規則對3個參數進行在線實時整定，滿足不同誤差和誤差變化率對3個參數的不同要求。

大多數模糊推理只著重不確定性現象和事物中的模糊性，未能考慮不確定性現象和事物的隨機誤差，推理系統輸入值有很大隨機性。由于模糊控制要確定精確的隸屬度函數，因此容易造成推理結果錯誤。

2.2 云模型

云模型是定性概念和定量表示之間的不確定性轉換模型，主要反映知識表示中的兩種不確定性。在眾多不確定性中，最基本和最重要的是模糊性和隨機性，針對概率論、模糊數學在處理不確定性方面的不足，研究了模糊性和隨機性兩者之間的關系[8]。

云的定義：設U是一個用精確數值表示的定量論域，A是U上的定性概念，若定量值x∈U，且x是定性概念A的一次隨機實現，x對A的隸屬度μ(x)∈[0,1]具有穩定傾向的隨機數，則稱μA(x)在U上的分布為云模型。

2.3 基于云模型的模糊推理PID控制器

筆者設計的控制器是將正態云模型引入到隸屬度函數，用正態云函數表示隸屬度，構成基于云模型的模糊推理PID控制器，可以兼顧模糊性和隨機性[9]，控制器結構如圖3所示。

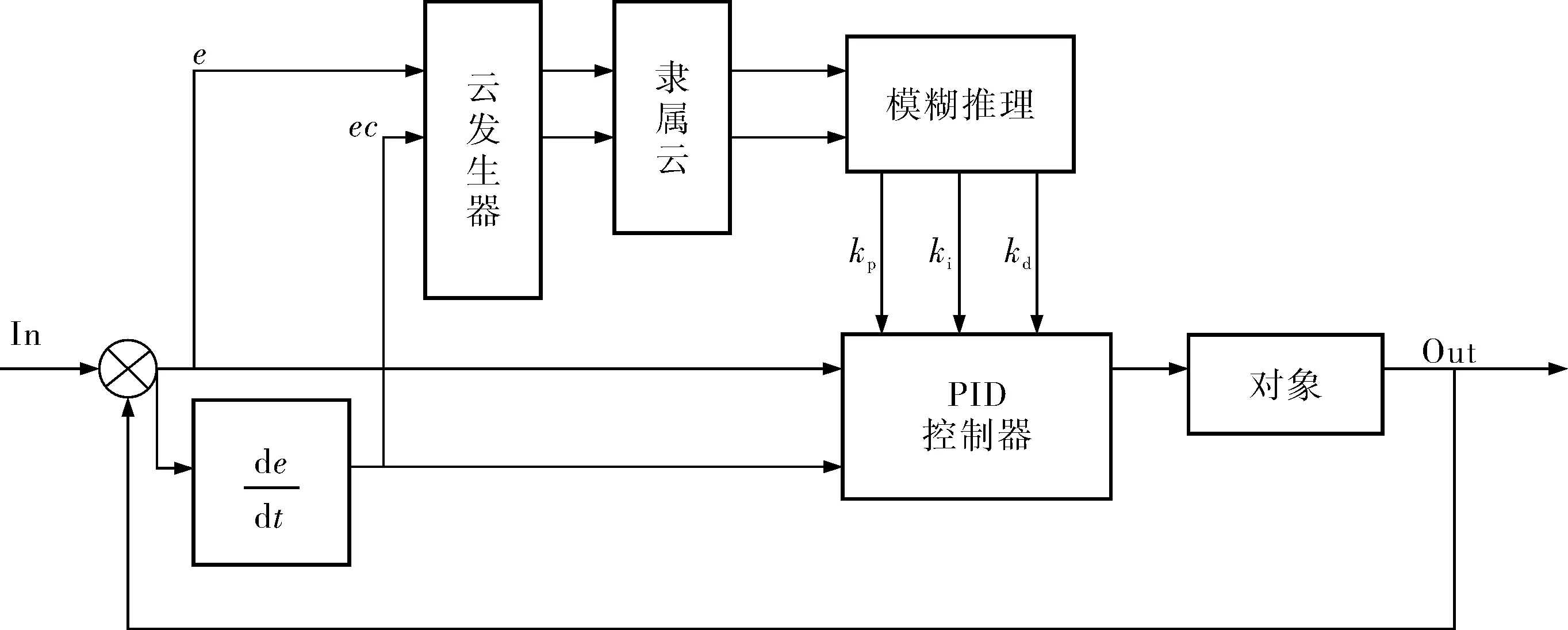
圖3 云模型模糊推理PID控制器結構框圖

正態云是一種是一種普通的適用云。設R1(E1,E2)表示服從一維正態分布的隨機函數，其中E1為期望值，E2為標準差，則有：

xi=R1(Ex,En)

Pi=R1(En,He)

由滿足上式的數據點(xi,μi)(i=1，2，…)構成的云模型稱為一維正態云模型，式中Ex、En、He是該云模型的3個重要數字特征，分別稱為一維云模型的期望、熵和超熵。

正態云發生器是由云的數學特征產生云滴的過程，如圖4所示。

圖4 正態云發生器的形成

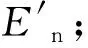
在模糊控制規則中，誤差為e、誤差變化率為ec，修正系數為kp，ki，kd，模糊子集為{NB，NM，NS，ZO，PS，PM，PB}，論域為e={-30，30}、ec={-60，60}。基于云模型的模糊推理PID控制器是以誤差e和誤差變化率ec作為輸入，將正態云模型引入模糊控制的隸屬度函數，根據每個正態云模型的隸屬度函數設計PID參數的模糊矩陣表，利用模糊規則進行模糊推理，查詢模糊矩陣表在線對PID參數進行調整。

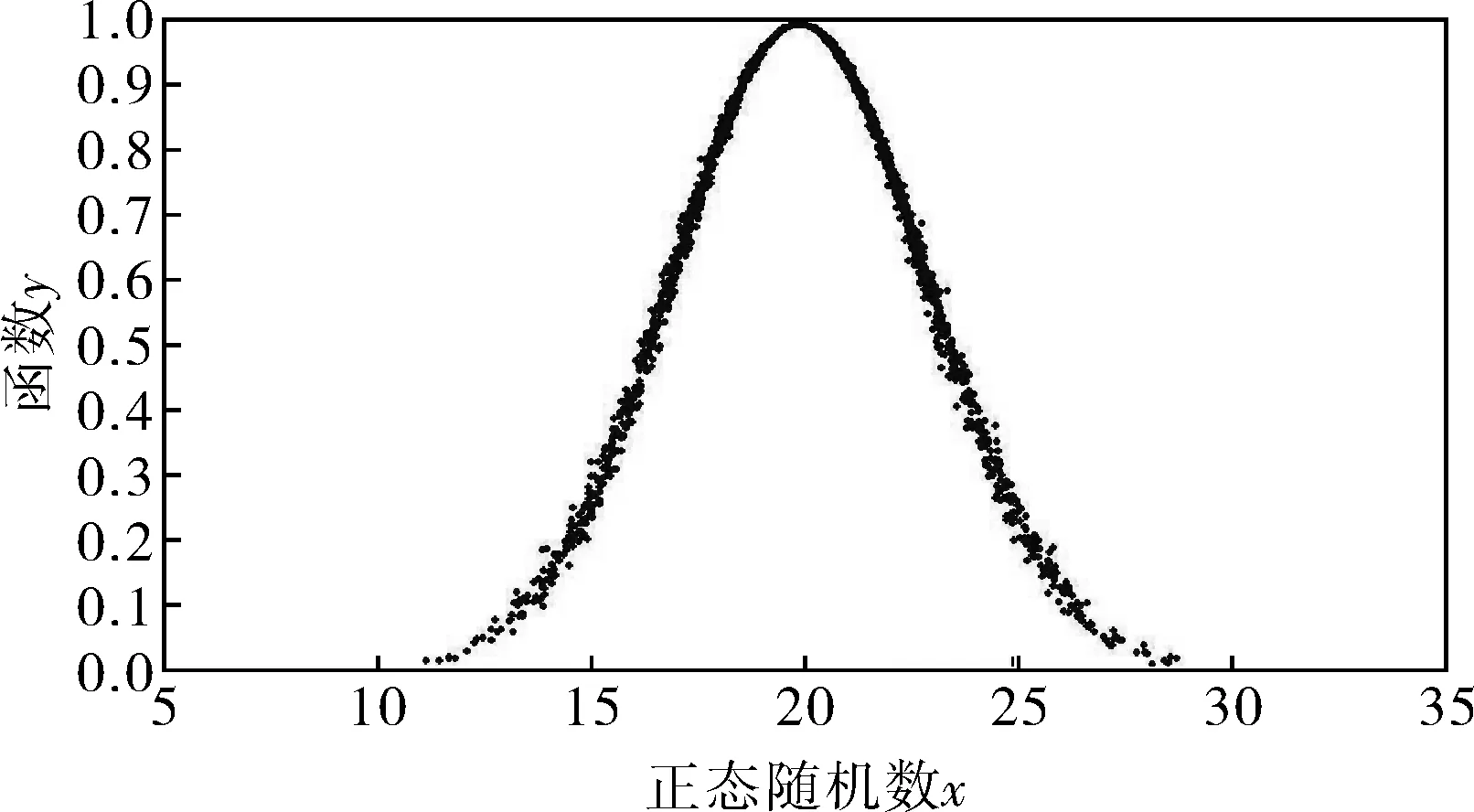
圖5 正態云模型

3 仿真分析

RT-LAB是一種全新、可擴展的基于模型的工程設計應用實時仿真平臺。通過RT-LAB可以直接利用Matlab/Simulink建立動態數學模型進行實時仿真。筆者運用RT-LAB仿真實驗平臺進行仿真驗證，根據RT-LAB建模方法建立風力發電系統模型，如圖6所示。

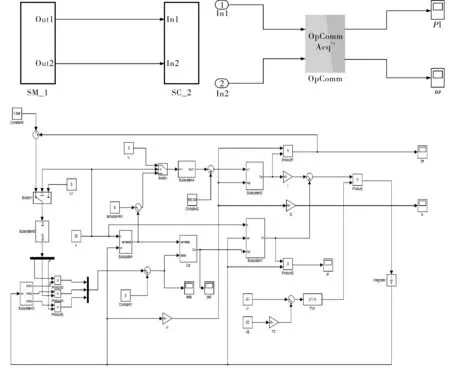
圖6 RT-LAB下搭建風力發電系統及SC、SM子系統

筆者以1.5MW變槳距風力發電機組為研究對象，在高于額定風速取初始風速為13m/s，20s時突變到14m/s。對模糊PID控制和云模型控制方法進行仿真比較，如圖7～9所示。

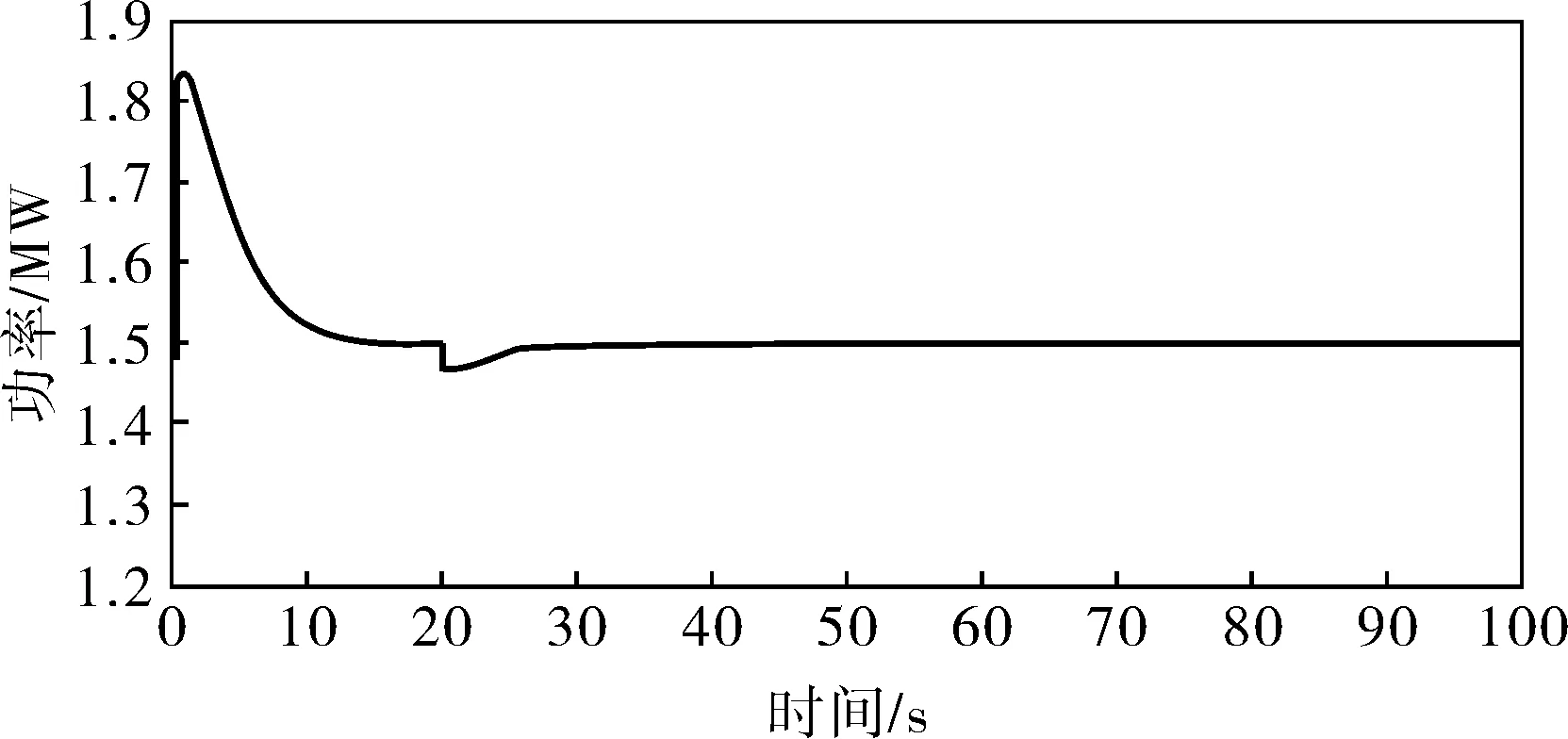
圖7 模糊PID統一變槳距控制的輸出功率曲線

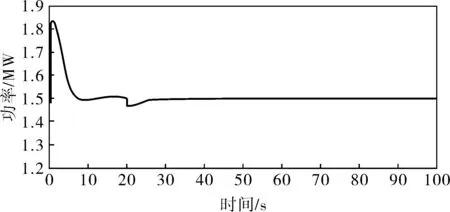
圖8 模糊PID獨立變槳距控制的輸出功率曲線

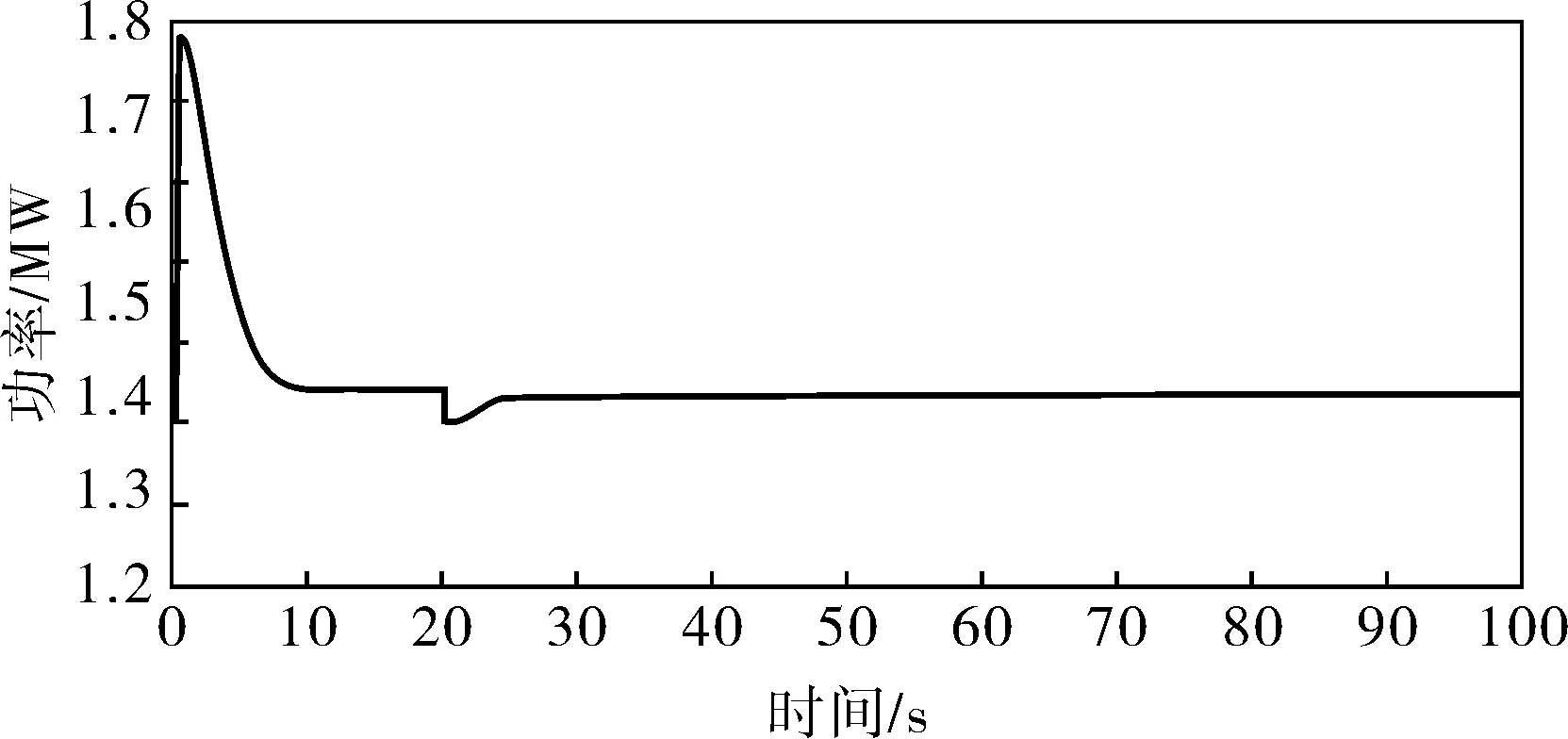
圖9 基于云模型的獨立變槳距控制的輸出功率曲線

仿真結果表明，在高于額定風速時，統一變槳距和獨立變槳距控制都能控制輸出功率穩定在額定功率附近，且在風速變化時也有較好的控制效果，但獨立變槳距控制的超調更小，穩定性更高。基于云模型的獨立變槳距控制比基于模糊PID的獨立變槳距控制效果更好，超調更小，響應速度更快，穩定性更好，控制效果更加理想。

4 結束語

分析了風電機組變槳距控制系統的運行特性和風切、塔影效應對風速的影響，并詳細介紹了云模型的概念和特征。采用方位角權系數分配的方法，設計了基于云模型的獨立變槳距控制系統，運用RT-LAB仿真實驗平臺對1.5MW風力發電機組進行建模仿真。仿真結果表明：在高于額定風速時，該系統超調小，響應速度快，穩定性強，可以有穩定的功率輸出，實現了系統的優化運行，取得了理想的控制效果。