數學教學中培養學生的創造性思維

何生財

【摘要】 創造性思維是各種思維優化組合的高效思維，通過它可導出新穎獨特、前所未有的思維成果，是造就創造型人才的飛躍性標志. 現僅結合本人的教學實踐，談談對學生創造性思維的培養的做法和體會.

【關鍵詞】 數學教學；創造性思維；教學實踐

在數學教學中，若能激發和引導學生在學習及解決問題的過程中，去主動地發現、探索自己或者他人所未發現、未解決的問題，創造新穎獨到的解法，提出新見解等創造性思維活動，不僅對開發學生的智力、提高分析問題和解決問題的能力具有重要意義，而且能影響學生的一生.

一、巧設疑問，激發創新欲望

在數學教學中，教師應該經常有意識地創設一些問題情境，把學生這種潛在的需求激發出來，使之產生創新的欲望.

例如，教學“圓的周長”時，教師設計如下矛盾沖突：用直尺直接測量一個圓的周長，你能不能想出一個好辦法來？（生1：把圓放在直尺邊上滾動一周，用滾動的方法測量出圓的周長. 生2：用繩子在圓上繞一周，再測出繩子的長短，得到這個圓的周長.）隨后，教師甩動繩系小球，形成一個圓，問：小球運動形成一個圓，你能用剛才的方法測量出圓的周長嗎？（學生面面相覷，面露難色）于是，教師抓住時機：“看來，用滾動、繩繞的方法可以測量出圓的周長，但卻有一定的局限性. 我們能不能探討出求圓周長的一般方法呢？”學生一下活躍起來，并經過討論和教師的引導，很快就得出求圓周長的一般方法. 通過教師施問創境，誘發學生主動參與問題解決的“再創造”過程，這樣就激起了學生的興趣和探究的強烈愿望.

二、利用“開放性”問題來進行創新思維訓練

開放性問題重在開發思維，促進創新，而其中解題用到的觀察、實驗、猜想、論證是科學思維方法，學習中應重視并應用.

開放性問題的種類很多，主要有：條件開放、結論開放、解題方法的開放.

1. 條件開放

條件開放探索題的明確特征是缺少確定的條件，問題所需補充的條件不是得出結論的必要條件，所需補充的條件不能由結論推出.

例：已知（x1，y1），（x2，y2）為反比例函數y = ■圖像上的點，當0 < x1 < x2時，y1 > y2，則k的一個值可為_______（只需寫出符合條件的一個k的值）.

解： 答案不唯一，只要符合k > 0即可，如k = 1，k = 2，…

2. 結論開放

給出問題的條件，讓解題者根據條件探索相應的結論，并且符合條件的結論往往呈現多樣性，或者相應的結論的“存在性”需要解題者進行推斷，甚至要求解題者探求條件在變化中的結論，這些問題都是結論開放性問題.它要求解題者充分利用條件進行大膽而合理的猜想，發現規律，得出結論.這類題主要考查解題者的發散性思維和所學基本知識的應用能力.

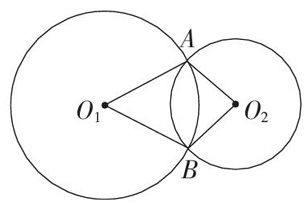
例：如圖，圓O1與圓O2相交于點A，B，順次連接O1，A，O2，B四點，得四邊形O1AO2B. 根據我們學習矩形、菱形、正方形性質時所獲得的經驗，探求圖中的四邊形有哪些性質.（用文字語言寫出4條性質）

性質1：________________________________；

性質2：________________________________；

性質3：________________________________；

性質4：________________________________.

解：是開放性問題，答案有許多，如：

性質1：相交兩圓連心線垂直公共弦；

性質2：相交兩圓連心線平分公共弦；

性質3：線段O1A = 線段O1B；

性質4：線段O2A = 線段O2B；

性質5：∠O1AO2 = ∠O1BO2；

性質6：……

三、創設“問題”情景，培養學生發現提出新問題的能力

“發明千千萬，起點是一問.” 數學的發展過程是一個不斷提出問題、解決問題的過程. 從培養學生創新性思維能力的角度看，提出問題比解決問題更重要. 在日常的數學學習中，學生沒有想到去提問題，也不知道怎樣去提問題. 而條件和結論不完備或不確定、解題策略多樣化的數學開放性問題具有很強的疑問性，能誘導學生猜測各種不同的條件、結論、思路，促使學生提出各種不同的問題，培養他們發現新問題的能力.

創造性思維的產生是多因素、多變量、多層次的交互作用促成的. 在數學教學中，要既精心組織發散性較強的問題，創設情景，促進智力探索，形成創造氣氛，又注重學生的心理和思維特征，激發探索興趣；既指導學生拓寬知識范圍，加深理解深度，廣吸知識營養，又促進學生夯實基礎知識，掌握基本技能，活用通性通法；既指導學生在思維活動中靈活運用多向思維，并注意各種思維方式的辯證性，又要求學生領會數學思想的規律和方法. 創造性思維的培養，是一項多變元的系統工程，有待于我們把握時代發展中思維發展的脈搏，去探索，去開拓.