巧用課堂中的典型錯誤提升課堂效率的若干策略
●
(東北師范大學南湖實驗學校 浙江嘉興 314000)
巧用課堂中的典型錯誤提升課堂效率的若干策略
●周立志
(東北師范大學南湖實驗學校 浙江嘉興 314000)
在課堂教學中,經常會出現大量的學習錯誤:對解法混淆運用;對結論掌握不全;對概念理解不透;……其中許多錯誤真實記錄了學生數學思維的過程.教師若能隨機應變,巧妙地利用這些“錯誤”,變廢為寶,則可以幫助學生從錯誤中走出來,同時引導學生進行自我反思與歸類,有效提高課堂的教學效率和學生的學習能力.本文結合筆者的日常教學加以闡述.
1 將錯就錯——讓錯誤彰顯精彩
當代科學家波普爾說:“錯誤中往往孕育著比正確更豐富的發現和創造因素.”學生在數學學習中出現錯誤是不可避免的,同時課堂上發生的錯誤也并非一文不值:它往往能暴露出學生的真實想法,反映出學生的思維能力,包含著有價值的成分.教師若能善于發現錯誤背后隱藏的合理價值,巧用錯誤,則能讓課堂妙趣橫生,充滿生成.

筆者在巡視時發現,犯錯誤的學生不是個別.這時候,做對了的學生在下面哄笑,那個出錯的學生一臉尷尬.筆者當場來個“順水推舟,將錯就錯”:“剛才去分母的這位同學的解法顯然是錯的,可我發現出錯的并非就此一人.有一部分同學也把分式的化簡當作分式方程來解了,解法雖然錯了,但也有這種方法的優點,那就是去掉分母來解,其解法簡捷明快,因此我們考慮能否利用方程來解呢?”整個班級頓時陷入了思考,成績較好的學生探究的聲音也很輕,顯得比較謹慎.顯然,學生們被難住了.筆者再及時跟進,予以提醒:“剛才‘當作’分式方程解是錯的,注意現在我說是‘利用’分式方程來解.”過了幾分鐘,有學生興奮地站起來:設這個分式等于一個字母.于是一個“另類”的解題過程就呈現了.

2(x-2)-2(x+2)=A(x+2)(x-2),

于是大家感覺用方程解法化簡分式的方法有創意,更重要的是這種“將錯就錯”得到的結果也讓剛才做錯的學生體面地化解了尷尬.
可見,教師要充分利用學生學習中出現的錯誤,鼓勵學生從多角度、全方位審視自己在學習活動中出現的錯誤,因勢利導.這種教學的效果遠遠勝于直接告訴學生一個正確的結論.
2 巧設陷阱——讓錯誤激發反思
英國心理學家貝恩布里奇說:“錯誤人皆有之,作為教師不利用是不可原諒的.”因此,教師可以有意識地選擇一些學生極易出錯的題目,設置“陷阱”,讓學生陷入歧途,產生思維沖突,從中可以誘導出學生在認知中的錯誤或片面觀點,有助于教師及時捕捉、弄清教學對象的認知特點,采取有效的教學措施,使教學具有針對性.
案例2反比例函數中的增減性一方面與一次函數有著相反的性質,另一方面增減性是不連續的,運用該知識點解題時學生極易出錯.筆者在期末總復習時就碰到一例.浙教版《數學》9年級上冊作業本(2)第32頁習題如下:

( )
A.y1
D.y1與y2之間的大小關系不能確定
學生解答時幾乎都選A,理由很“充分”:k=-1,y隨x的增大而增大.對于這樣的局面,筆者沒有急于給出正確結論,而是引導學生回顧已學知識:

學生一一回答,其中筆者特意將增減性這一性質寫成2行:
當k>0時,y的值隨x的增大而減小.
接著,筆者有意識地設計了以下一組問題,讓學生“陷入歧途”:

由于有了前面學習反比例函數的經驗,學生馬上回答:y1>y2.

學生異口同聲回答:y1 學生很響亮地回答:y1 “誤導”很成功! 學生依舊響亮回答:y1>y2! 這時,筆者注意到平時善于思考的學生M面露困惑,她站起來講述了想法,學生們都傻眼了:當x1=-1時,y1=-2;當x2=1時,y2=2,此時y1 教室馬上由熱鬧陷入沉思.不久,有學生頓悟:“老師,我們忽略了‘在每一象限內’這句話.”筆者馬上用彩筆在先前故意分段留有空白的地方補上:在每一象限內.至此,學生對錯題中的錯因心知肚明,錯誤不教而解. 美國數學家波利亞說過:“錯誤中往往孕育著比正確更豐富的發現和創造因素,發現的方法就是試錯的方法.”該案例的教學中如果只是機械地告訴學生不要忽略“在每一象限內”這一條件,那學生就只能在教師的“諄諄告誡”下僵化、被動地接受知識,其結果是將會成為技能低下、缺乏質疑精神和探索精神的書呆子.因此,教師在錯誤分析的過程中不必擔心學生犯錯,而應該盡可能把學生頭腦中的問題“擠”出來,把思考問題的思維缺陷暴露出來,以此來激發學生重新反思錯誤,進而達到糾錯的目的. 布魯納說:“學生的錯誤都是有價值的.”學生在解題時出錯的原因是多樣的,教師應立足學生,從多樣的錯誤中去發現學生思維的漏洞、誤區,順勢而上,順藤摸瓜,引導學生找到錯誤根源,讓學生在錯誤中尋求到正確的方向,促使學生的思維水平有層次、有步驟地向更優化的方向發展. 案例3學生在運用三角函數定義解題時,容易受到定義學習過程中構造直角三角形的影響,得到錯誤結論.筆者在一次作業講評課中就碰到一例: 圖1 (該學生的回答馬上贏得了部分學生的“認可”.) 師:哦.那我們是不是可以認為如果不是直角三角形,銳角就沒有三角函數值呢? 教室突然靜了下來,剛才“認可”的學生也開始打開書本. 生2(激動地):不對,不是直角三角形的銳角也有三角函數值,比如教材第12頁作業題有很多銳角就有三角函數值. 生3:而且我發現書本上的定義告訴我們只有用邊去求三角形函數值時才需要在直角三角形中. 生3(自信地):僅僅得到∠B=30°而已,其他的角是多少度不能得到. 因為學生對銳角三角函數概念的本質掌握不到位,造成思維定勢,進而得出直角三角形的結論.可見,當學生暴露錯誤苗頭時,教師不要急于給出正確的結論與過程,而應通過對學生的錯誤展開刨根究底的追問,引導學生去發現、糾正,從而使學生的知識主動建構,形成了正確而完整的知識體系. 杜威曾說過:“失敗是有教導性的,真正懂得思考的人,從失敗和成功中學得一樣多!”因此,教師除了將學生中的錯誤做典型分析外,還應該引導學生善于將平時解題所犯的錯誤進行收集歸類與反思.比如,教師可以要求班級每個學生準備一本《數學糾錯本》,專門記錄平時做錯的題以及錯誤的過程,指導學生將解錯原因化歸為概念出錯還是計算、應用出錯,并在錯題后附上自己做錯的原因.而對于相同類型的錯題,則引導學生刪選出最典型的錯題,訂正出正確的過程.這種糾錯的方式,讓學生在自我分析的反思過程中加深了對薄弱知識的理解與掌握. 此外,教師在每一章節結束后,利用1~2個課時在班級進行糾錯與反思心得交流活動,在活動中展示出最深刻的反思或最典型的錯誤類型,起到借鑒、共勉的效果. 案例4學生F在一次交流中講道: 這樣幽默地講述,留給學生們的印象是極其深刻的.這樣的活動激發了學生進行錯題摘錄的興趣,同時也潛移默化地讓學生養成“平時有空翻一翻、考前認真看一看”的習慣,從而達到錯一次而收獲十倍的效果. 所謂錯誤,是指師生在認知過程中的偏差或失誤,錯誤伴隨著教學的始終,而且錯誤是無法避免的.教師在遇到錯誤時,應針對不同原因,變廢為寶,巧用這一生成的寶貴教學資源輔助課堂教學,幫助學生靈活糾錯,努力讓錯誤成為數學課堂教學的一個亮點,成為重要的課程資源,讓其閃現創新的火花,發揮應有的價值. (注:本文為2012年度教育部人文社科一般級項目“智慧型學校的實踐研究與理論分析——依托大學與中小學合作的學校改進的行動研究”(編號:12YJA880057)的研究成果之一.) [1] 教育部.義務教育數學課程標準:2011版[M].北京:北京師范大學出版社,2012:8. [2] 李建新.讓錯誤成為教學的亮點[J].教育革新,2011(11):17-18. [3] 吳剛妹.暴露錯誤成就精彩課堂[J].新課程研究:上旬刊,2012(5):13-14. [4] 陳銳.樹立正確的學生錯誤觀——以教學中的錯誤為例[J].考試周刊,2012(30):20-21.

3 順藤摸瓜——讓錯誤無處遁形

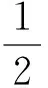
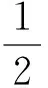
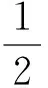
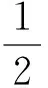
4 反思歸類——讓錯誤漸行漸遠

