初中數學有效教學三部曲

陳浩

【關鍵詞】初中數學 有效教學 情境 問題 應用

【中圖分類號】G 【文獻標識碼】A

【文章編號】0450-9889（2013）08B-0080-01

要構建有效的數學課堂教學，還得從學生這一主體出發，從學生的興趣出發，結合生活來引入知識的學習，充分發揮教師的主導作用，以問題為導向，讓學生經歷問題的分析和解決過程，在掌握知識的基礎上應用知識來解決問題，培養學生的實踐能力。這樣的數學課堂才會更加有效，有利于促進學生的全面發展。

一、創設生活情境，引入知識探究

對教師而言，初中數學教材中所呈現的知識較為簡單，從代數的有理數到方程，從幾何的一般圖形特點到圖形的面積計算等都是基礎，而對剛上初中的學生來說，這些知識都具有一定的抽象性。因此，如果教師在教學中依舊以灌輸式的方式來傳授學生知識，學生的興趣就會被削減，無法更好地理解其中所涉及的概念、公式等，從而讓數學學習效率降低。相反，如果教師能從學生的生活實際出發，以直觀的情境來引入新知識，促進學生形成從直觀到抽象的過渡，借助問題來啟發學生的思考，不僅有助于激發學生的學習興趣，還能更好地引導學生理解相關的概念、公式、定理等。

如在“正負數”的學習過程中，從學生的零花錢的收入、支出說起；在“一元一次方程”的學習中，以體育運動中的路程問題來導入都能較好地激發學生的學習興趣。但在導入過程中教師要注重根據教學目標來提出問題，啟發學生的思維，從而進入新知的探究過程。又如，在全等三角形的學習過程中，教師先給出一個三角形（通過情境展示生活中的三角形物后轉化而來），然后引導學生根據三角形三條邊的長度、三個角的大小畫出并剪下該三角形，同桌對比后，教師提問：“兩個三角形的邊和角有什么相同點？”通過這樣的問題，讓學生初步感受“全等”的概念，從而為新知的學習奠定基礎。

二、提出問題引導，合作分析解決

教師通過情境激發學生的學習興趣后，在教學過程中需要借助問題來引導學生對所要學習的知識從簡單到復雜、由淺而深地不斷探究，在這個過程中，借助問題，形成師生間、生生間的互動，有利于問題的分析和解決。同時，借助互動和反饋，教師能及時了解學生的學習狀態，進而調整教學策略，推動課堂教學的發展。因此，在初中數學課堂教學中，教師要注重從學生實際出發，結合教學目標和教學內容來提出具有層次性的問題，引導學生進行合作探究。

如，在“位似圖形”的教學中，我先提出問題“什么叫位似圖形、位似中心、位似比？”引導學生自主閱讀教材，初步理解概念，在學生觀察圖形后提出問題：“位似圖形的位似中心與這兩個圖形有什么位置關系？任取一對對應點，度量這兩個點到位似中心的距離。它們的比與位似比有什么關系？再換一對對應點試一試。”引導各小組學生拿出準備好的位似圖形通過觀察、測量試驗和計算，討論、交流而得到“位似圖形對應點到位似中心的距離之比等于相似比”的結論，教師再引導總結，補充得出“位似圖形的對應點和位似中心在同一條直線上，它們到位似中心的距離之比等于相似比”的結論。這樣的學習過程，學生更多的是在教師的引導下完成，而不是被動接受的過程，因此知識的構建更深入。

三、解決實際問題，培養實踐技能

學生通過討論、交流初步構建了知識后，教師就要借助具體問題來引導學生進行解決，從而提高學生解決問題的能力。

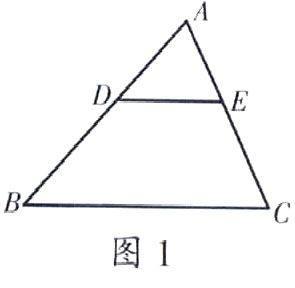
如在“位似圖形”的教學中，教師用幻燈片出示問題：如圖（1），D、E分別是AB、AC上的點。（1）如果DE∥BC，那么△ADE和△ABC位似圖形嗎？為什么？（2）如果△ADE和△ABC是位似圖形，那么DE∥BC嗎？為什么？小組討論如何解這道題。問題1：證明位似圖形的根據是什么？需要哪幾個條件？問題2：已知△ADE和△ABC是位似圖形，我們根據什么又能得出什么結論？對于問題1教師要指導學生根據位似圖形的定義，知道位似圖形需要滿足兩個條件①△ADE和△ABC相似；②對應點所在的直線交于一點。而對于問題2則根據位似圖形的性質得出：①對應點和位似中心在同一條直線上；②它們到位似中心的距離之比等于相似比。最后再求證。

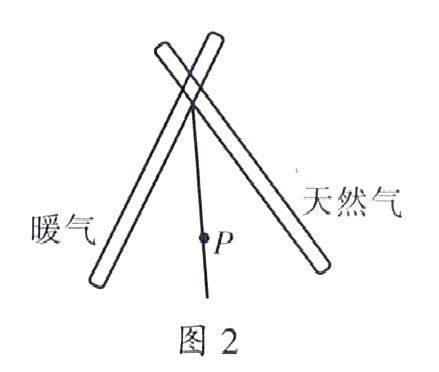
再如，在“全等三角形”的學習后，教師提出問題：小明家居住在一棟居民樓的一樓，剛好位于一條暖氣管道和天然氣管道所成角的平分線上的P點，要從P點建兩條管道，分別與暖氣管道和天然氣管道相連（如圖（2））。問題1：怎樣修建管道最短？問題2：新修的兩條管道長度有什么關系？畫圖看一看。通過這樣的實際問題來引導學生在分析和解決問題中鞏固全等三角形的概念，并能根據所學知識來解決問題，促進學生實踐能力的提高。

總之，在新課改背景下，教師在數學課堂教學中要注重突出學生的主體性，通過革新教學觀念和教學模式，通過情境導入、問題分析、應用實踐來促進學生經歷數學學習的過程，促進學生的知識構建和技能培養。

（責編 林 劍）