基于RVM回歸的姿控系統多故障檢測

胡迪， 董云峰

(北京航空航天大學宇航學院，北京 100191)

0 引言

衛星姿控系統是保證衛星平臺正常運行的重要系統之一。一般來說，衛星姿態控制系統由敏感器、執行機構以及姿控中心計算機組成，敏感器有很多種，如地球敏感器、陀螺和星敏感器等，執行機構一般有反作用輪、推力器和磁力矩器等，姿控中心計算機一般采用主備份冗余結構實現。當一個或多個敏感器/執行機構發生故障后，會對衛星姿控系統造成重大影響，輕則影響控制精確度，重則導致整星失效。由于姿控系統部件眾多，其故障發生情況往往是多種故障的耦合效應。因此對衛星敏感器和執行機構的單一故障以及多發性或并發性故障進行診斷具有重要意義。

故障診斷是判定故障發生的位置和大小，而故障檢測是故障診斷的第一步。

對于航天器來說，一般采用基于模型的方法進行故障診斷，如采用建模的方法［1］實現對飛船推進系統的故障診斷，或者采用觀測器［2－3］實現對飛輪故障的檢測和恢復等。通過數學建模的方法實現航天器故障診斷，受限于建模的精確度，并且不確定因素會導致誤判，而通過基于信號處理和知識的方法［4］進行在軌故障診斷，往往受限于星載計算機的性能。

為了有效避免數學建模的誤差，目前有學者提出通過對衛星在軌運行數據采集，采用最小二乘回歸支持向量機(least square support vector regression，LSSVR)進行模型辨識，實現對部件的離線建模。同時通過在軌數據的離線建模也可以有效實現對干擾的估計建模。文獻［5］采用LSSVR對姿控系統測量部件進行建模，通過求解半正定規劃(semi－definite programming，SDP)問題來優化支持向量回歸(support vector regression，SVR)的核空間，并驗證了該方法具有很高的建模精確度，但其假定系統只有測量系統故障，沒有考慮到執行機構系統也會發生故障的情況。文獻［6］采用LSSVR對姿控測量系統建立觀測器，從而可以檢測故障，雖然考慮了不確定因素，但其依然受建模的精確度影響，并且采用LSSVR進行模型辨識或建立觀測器，需要調節LSSVR模型的參數，其對辨識結果的精確度影響非常大。

目前學者針對某一部件失效后進行故障檢測和診斷，如采用濾波器的方法［7］或神經網絡的方法［8］實現對推力器的故障診斷，采用建立動態神經網絡觀測器的方法實現飛輪的故障檢測［4］，采用無跡卡曼濾波(unscented kalman filtering，UKF)等方法實現姿態確定系統的故障診斷［9］等。

考慮到衛星姿控系統各個部件均可能發生故障，本文通過對各個部件的歷史數據流向分析，采用相關向量機(relevance vector machine，RVM)分別對敏感器和執行機構進行回歸辨識，離線建立辨識模型，在軌運行后通過部件輸出與辨識模型輸出產生殘差，并進行評價，從而實現姿控系統的多故障檢測。

1 系統描述

考慮如下姿態控制系統非線性狀態方程［6］，即

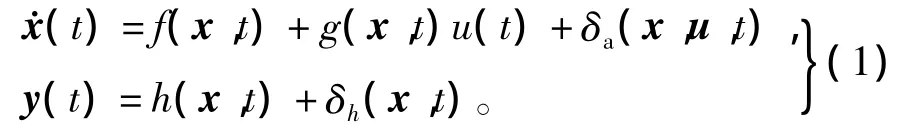
式中:x(t)∈Rn為系統的狀態向量;u(t)∈Rm為系統的控制力矩輸入向量;f(x，t)和g(x，t)的定義可參考文獻［6］;δa(x，u，t)為執行機構故障;δh(x，t)為測量系統故障;h(x，t)為狀態向量的測量函數。

考慮每個執行機構和測量部件有不同的故障模式，并且故障發生情況具有多發性和并發性的特點，即在同一時間內或同一時刻可能發生兩種或兩種以上的故障，因而對于某個部件發生故障后，需要檢測出哪個部件發生故障，然后才能進行某個部件單機的故障診斷，本文通過引入相關向量機建模實現姿控系統多故障檢測。

2 基于RVM的回歸建模

相關向量機是［10－12］基于稀疏貝葉斯學習(sparse bayesian learning，SBL)方法，將高斯過程的貝葉斯推理方法應用到支持向量機中，通過類似于支持向量機(support vector machine，SVM)核轉化的線性參數估計的方法，得到概率分布的結果。他具有SVM的特點，并且擴展了核函數的要求，使核函數不受Mercer條件的限制，因此可選核函數的范圍更廣，更適合于函數的回歸。相關向量機回歸參數的調節比SVM更少，性能比SVM更優，并且已經應用于機械軸承故障診斷［13］。

對于回歸問題，即給定一系列輸入和相應的輸出，求解系統的模型問題。設輸入樣本為n維向量，某區域m個樣本及其值表示為(x1，y1)，…，(xm，ym)∈Rn×Rm，則回歸函數為

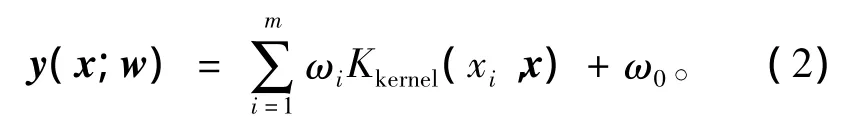
式中:x=［x1，x2，…，xm］為輸入樣本;w=［ω1，ω2…，ωm］T為權值;ω0為閥值;Kkernel(xi，x)為核函數。

對于新的輸入x，通過回歸函數預測輸出y，而觀測的輸出則被認為是真實值受獨立高斯噪聲污染后的輸出，即

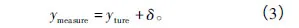
式中:δ為獨立的附加高斯噪聲，服從δ～N(yture，σ2)分布;ytrue為真實值;ymeasure為測量值，根據貝葉斯推理和獨立性假設，可得標準似然函數為

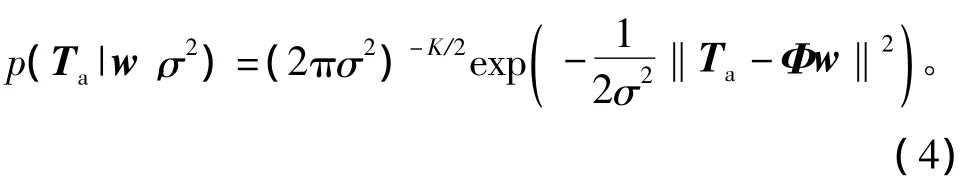
式中:Ta=［δ1，δ2，…，δn］T;Φ 為 n ×m 階矩陣，Φij=Kkernel(xi，xj)，i=1，2，…，n，j=1，2，…，m;K 為超參數的個數。

對于多權值的回歸模型，其最大似然會得到過擬和的結果，而在相關向量回歸模型中，通過使用Bayesian框架，使模型具有泛化性，參數的先驗分布為

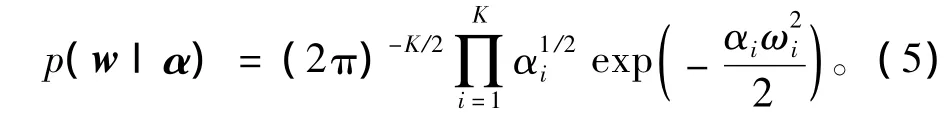
式中 α=［α1，α2，…，αK］為超參數。

在先驗分布和似然分布的基礎上，權值的后驗分布可由Bayesian推理求得，得到其后驗分布為

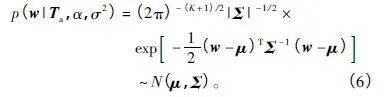
其中后驗均值和方差分別為

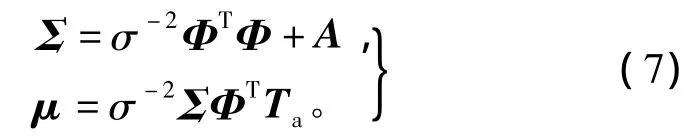
式中 A=diag(α1，α2，…，αK)。

在實際計算過程中，許多權值的后驗分布趨于零，在相關向量機的回歸模型中，非零的權值代表數據中的原型樣本，這些稱為“相關向量”。

式(3)中的目標輸出似然分布可以通過對權值進行邊緣積分求得，即

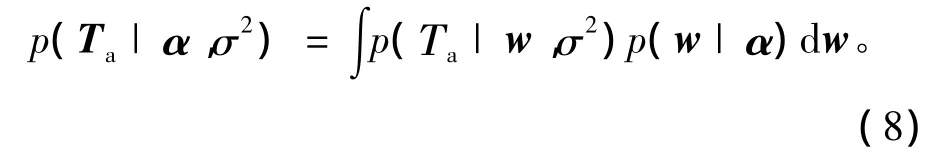
從而可得到超參數的邊緣似然分布，即

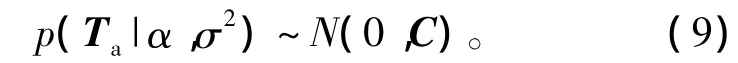
式中 C=σ2I+ΦA－1ΦT，I為單位矩陣。

對于一組新的輸入x*，其相應輸出T*的預測分布滿足高斯分布p(T*|Ta)～N(μ*)，其中

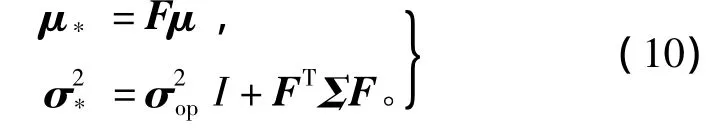
式中:F=［Φ1(x*)，Φ2(x*)，…，ΦK(x*)］T，Φi(x*)=Kkernel(x，x*)，i=1，2，…，K;為對式(4)的極大似然估計，決定了權重的最優值。

3 衛星姿控系統部件回歸建模

建模精確度是基于模型的故障診斷方法的核心，通過建立精確的回歸模型，可以有效實現故障檢測及診斷。

本文在某高軌衛星正常模式下，采用地球敏感器(地敏)、太陽敏感器(太敏)和陀螺進行姿態確定，采用反作用輪進行姿態控制。考慮到地球敏感器和太陽敏感器的數據輸入均為天體位置的矢量，因此本文僅考慮對太陽敏感器和陀螺的辨識建模。對于執行機構，本文考慮反作用輪辨識建模，可以推廣到其他執行機構。

本文采用數學模型與辨識模型的差值表征辨識模型的精確性。

3.1 太陽敏感器回歸建模

太陽敏感器分為數字式太陽敏感器和模擬式太陽敏感器，本文考慮數字式太陽敏感器，其根據太陽光線在碼盤上的光照情況計算太陽光與測量狹縫間的夾角。

由于太陽敏感器需要知道太陽位置，而太陽位置計算與軌道衛星運行軌道相關，因此設定軌道根數集為:半長軸為42164 km;偏心率為零;軌道傾角為0°;升交點赤經為0°;近地點幅角為0°;真近點角為 30°。

考慮衛星數字太陽敏感器的其中之一安裝在+X面，安裝矩陣為

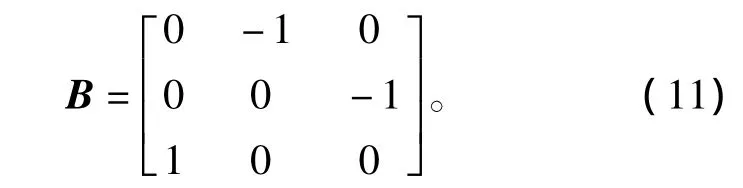
為正確辨識太陽敏感器的模型，需要對太陽敏感器的歷史輸入輸出數據進行分析。太陽敏感器模型的輸入為太陽矢量，輸出為太陽敏感器測量角。衛星姿控系統正常運行600 s，提取前400 s數據用于訓練模型，后200 s數據用于測試辨識模型是否正確。

分別采用LSSVR和RVM的建模誤差對比如圖1所示。

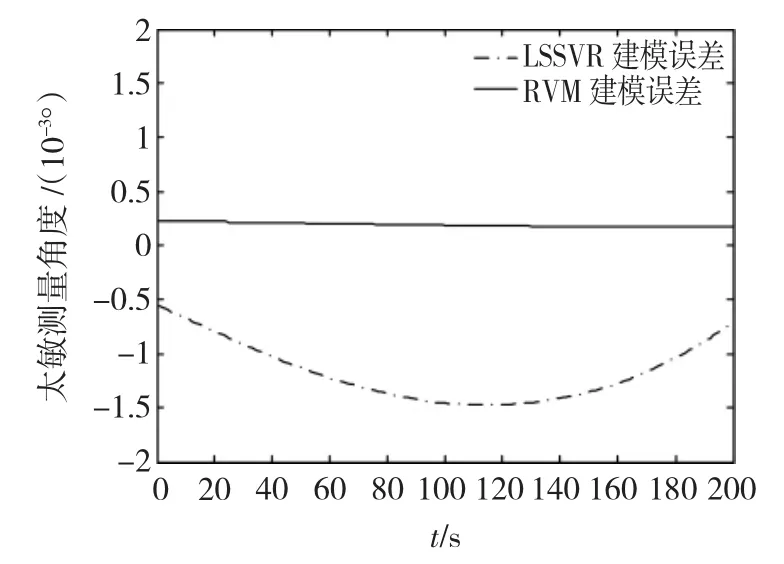
圖1 太敏LSSVR和RVM建模誤差對比Fig.1 Model error between LSSVR model and RVM model of digital sun sensor

由圖1可知，二者建模誤差均非常小。LSSVR辨識結果與LSSVR的參數調節有關，最大有0.0015°左右的差別，而RVM的辨識精確度比LSSVR高一個數量級，RVM辨識結果明顯優于LSSVR辨識結果，可用于在軌故障診斷。

3.2 陀螺回歸建模

考慮陀螺為3+1S陀螺組件，其中3個沿衛星三軸正交安裝，S陀螺為斜裝用于備份。本文在仿真時不考慮S軸陀螺。只考慮三軸正交安裝的陀螺，每一個陀螺測量一個軸的角速度。

陀螺測量的是衛星相對于慣性姿態的角速度，衛星干擾存在時會對星體產生擾動，可通過陀螺反映出來。為了更為準確地表征陀螺的模型，將衛星動力學模型和陀螺本身模型一同考慮，因此陀螺建模時，其輸入為反用輪的力矩指令，輸出為星體的角速度。

衛星姿控系統正常運行600 s，前面400 s為模型訓練，后200 s為模型測試。

分別采用LSSVR和RVM的建模誤差對比如圖2所示。

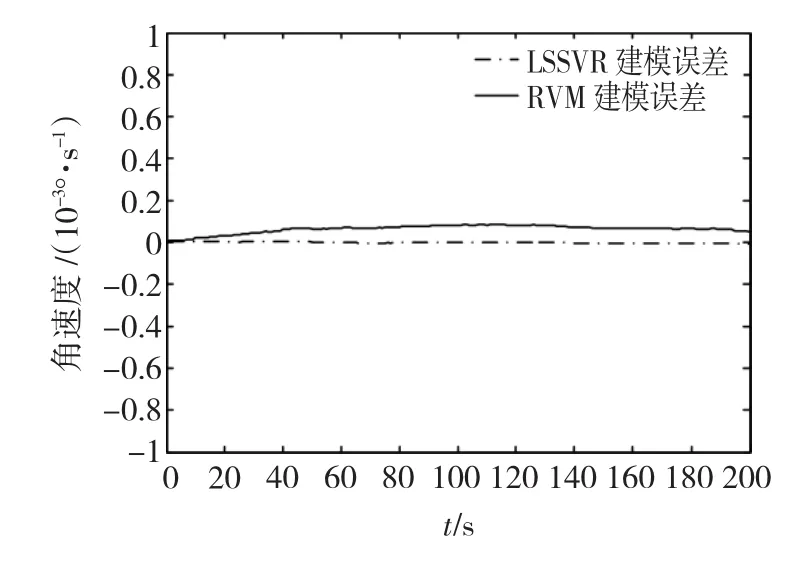
圖2 陀螺LSSVR和RVM建模誤差對比Fig.2 Model error between LSSVR model and RVM model of gyro

由圖2可知，二者建模誤差非常小，LSSVR的辨識結果比RVM要好，但可以看出，兩者的辨識精確度都高達1 ×10－4°/s，最大差值也只有0.001°/s，因此可以忽略。利用RVM辨識模型能準確反映出陀螺的數據狀態，可用于姿控系統故障診斷。

3.3 反作用輪回歸建模

反作用輪沿三軸正交安裝，整星為零動量系統。其中，斜裝的反作用輪用于備份，此處不考慮。

反作用輪的輸入為控制指令、電機電流，輸出為反作用輪的轉速，利用這3個信號可以進行模型辨識和建模。

分別采用LSSVR和RVM的建模誤差對比如圖3所示。

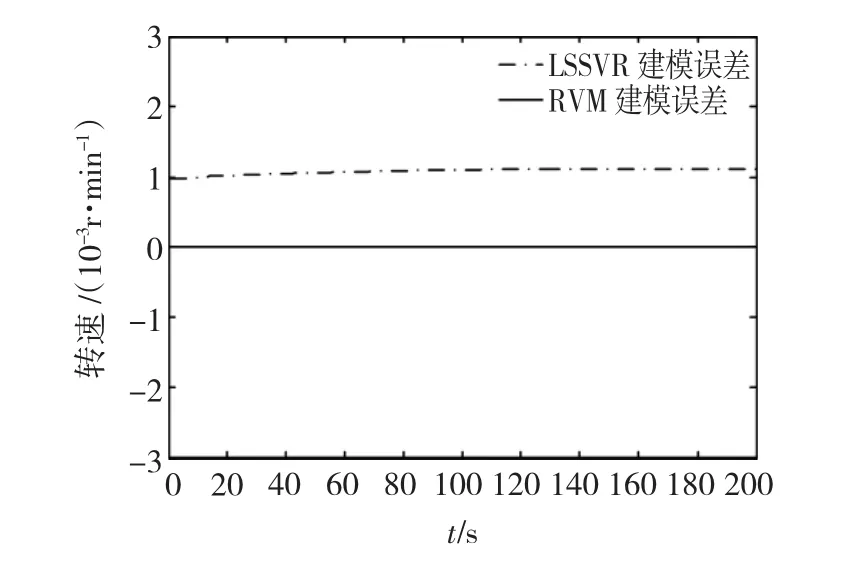
圖3 反作用輪LSSVR和RVM建模誤差對比Fig.3 Model error between LSSVR model and RVM model of reaction wheel

由圖3可知，LSSVR辨識的模型與仿真模型的差值為0.001 r/min，而RVM辨識差值幾乎等于零，因此RVM比LSSVR更能準確反映出反作用輪的工作狀態，可以用于姿控系統故障診斷。

4 衛星姿控系統多故障檢測

某同步軌道衛星在正常模式下，采用反作用輪進行姿態控制，采用太敏、地敏和陀螺進行姿態確定，因此整個姿控系統的故障檢測即是對太敏、地敏、陀螺和反作用輪進行多故障檢測。

由于衛星的故障具有并發性和多發性，在某一時刻陀螺和反作用輪可能會同時發生故障，或者在某一段時間內敏感器和執行機構同時發生故障，因此需對姿控系統進行多故障檢測，用于區分敏感器故障和執行機構故障，檢測完成后由各部件故障診斷算法完成某個部件的故障類型判定。

圖4為某同步軌道衛星在正常模式下的系統級故障檢測原理。利用上一節提出的RVM回歸進行模型辨識后，將辨識模型加入姿控系統中，與部件輸出數據形成殘差，進而評價殘差，從而實現故障診斷。

圖4 衛星姿控系統故障診斷示意圖Fig.4 The schematic of satellite attitude control system fault diagnosis

殘差評價可采用殘差加權平方和法，第k+1時刻的故障檢測判別函數值L(k+1)［14］為

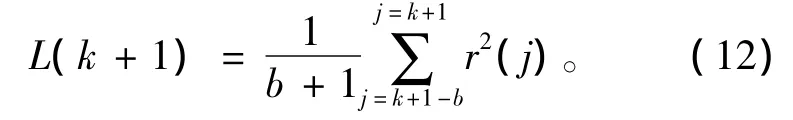
式中:b為選定的數據窗長度;r(j)為測量數據與辯識模型數據的殘差。從而故障檢測器可表示為

式中ε0為選定的檢測門限值，此值應參考部件無故障時的殘差選取。

5 仿真結果與討論

利用MATLAB對姿控系統建模，根據正常數據對太陽敏感器、陀螺和反作用輪進行離線訓練，并進行模型辨識，將辨識好的模型加入姿態控制系統。

為了反映衛星單一故障以及多發性和并發性故障，設計以下幾種工況用于測試，分別為太敏故障、反作用輪故障、陀螺與反作用輪同一時間段發生故障以及太敏與反作用輪同一時刻發生故障。其中，太敏輸出為太敏測量的角度，陀螺為Y軸陀螺輸出的角速度，反作用輪為反作用輪A的轉速。

5.1 太敏單一故障診斷

工況1，設定太敏在400 s時發生常值增大故障，陀螺和反作用輪正常，仿真結果如圖5所示。

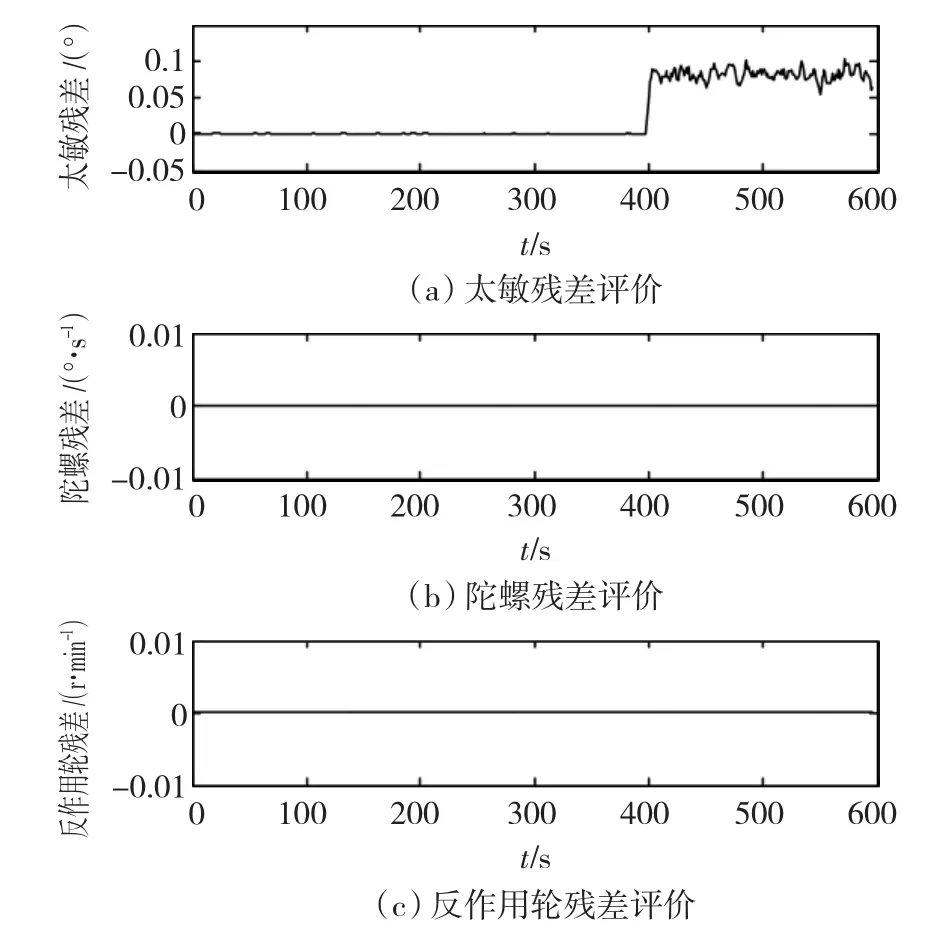
圖5 工況1殘差評價比較Fig.5 Residual evaluation of scenario 1

由殘差評價可見，RVM和LSSVR均檢測到太陽敏感器在400s時發生了故障，而陀螺和反作用輪沒受到干擾，故障診斷結果與預設一致。

5.2 反作用輪A單一故障診斷

工況2，設定反作用輪在500 s時發生故障，沿X軸方向的反作用輪發生軸承卡死的故障，陀螺和太敏不發生故障，仿真結果如圖6所示。

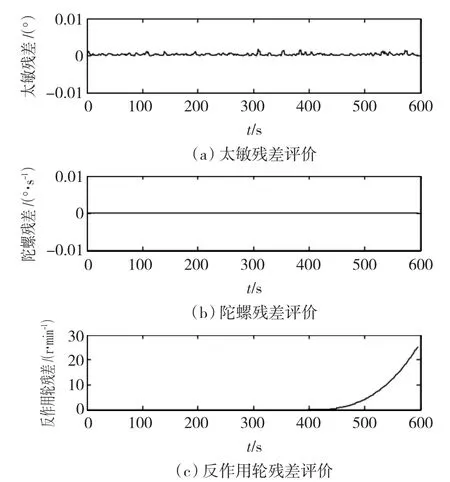
圖6 工況2殘差評價比較Fig.6 Residual evaluation of scenario 2

由圖6可以知，在500 s時反作用輪A的轉速殘差發生了突變，表征有故障發生，而陀螺和太敏測量數據的殘差沒有發生變化，因此故障診斷結果也與預設值一樣。

5.3 Y軸陀螺與反作用輪A多發性故障診斷

工況3，設定沿Y軸方向的陀螺在300 s時發生常值增大故障和沿X軸方向的反作用輪在400 s時發生摩擦力矩增大故障，仿真結果如圖7所示。

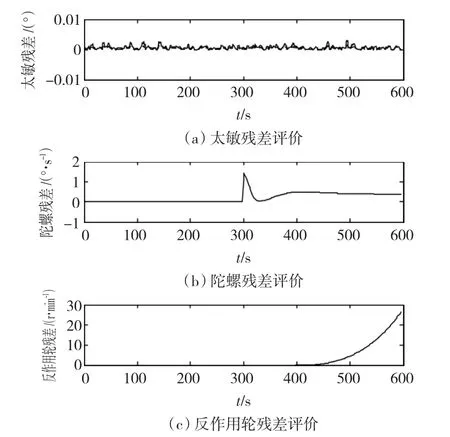
圖7 工況3殘差評價比較Fig.7 Residual evaluation of scenario 3

由圖7可知，在300 s時Y軸陀螺發生故障，在400 s時反作用輪A發生故障，而太敏殘差一直為零，因此故障判定與預設一致。

5.4 太敏與反作用輪A并發性故障診斷

工況4，假定太敏與反作用輪在400 s時同時發生故障，太敏發生常值增大故障，沿X軸方向的反作用輪故障為反電動勢增大，仿真結果如圖8所示。

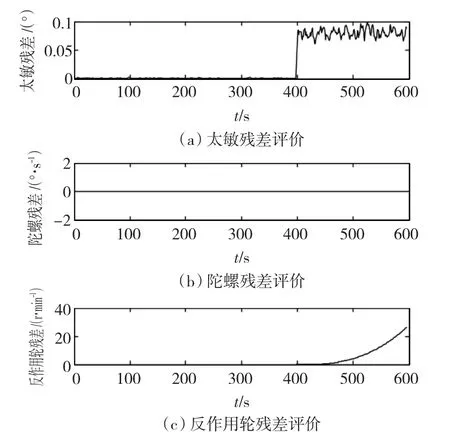
圖8 工況4殘差評價Fig.8 Residual evaluation of scenario 4

由圖8可知，在400 s時同時發生了兩種故障，一種是太敏故障，一種是反作用輪故障。由殘差評價也可知，通過RVM實現模型辨識，可以實現并發性故障診斷。

6 結語

本文通過RVM回歸對衛星姿控系統的敏感器和執行機構進行離線回歸建模，根據正常數據對辨識模型進行測試，在軌運行時考慮敏感器和執行機構均可能發生故障，采用辨識模型與仿真模型形成殘差輸出，通過加權平方和對殘差進行評價，實現衛星姿控系統單一故障診斷和系統級故障診斷。仿真結果表明，RVM回歸較LSSVR回歸可以有效實現對部件進行回歸建模，通過回歸建模不僅可以實現在軌衛星姿控系統單一故障診斷，也可以實現并發性和多發性故障診斷，為單機故障診斷提供先決條件，降低故障診斷的錯誤率，提高在軌故障診斷的實時性。因此，該方法可用于工程實踐中對部件模型進行辨識，從而實現故障診斷。

［1］寶音賀喜格，姜興渭，黃文虎.基于模型的故障診斷方法在飛船推進系統中的應用［J］.推進技術，1999，20(4):5－8.BAOYAN Heshig，JIANG Xingwei，HUANG Wenhu.Application of model based fault diagnosis method to propulsion system of spacecraft［J］.Journal of propulsion technology.1999，20(4):5－8.

［2］田科豐，李智斌基于自適應觀測器的飛輪故障診斷方法［J］.華中科技大學學報:自然科學版，2009，37(S1):184－186.TIAN Kefeng，LI Zhibin.Reaction wheel fault diagnosis based on adaptive observer［J］.Journal of Huazhong University of Science and Technology:Nature Science Edition，2009，37(S1):184－186.

［3］金磊，徐世杰.基于擴張狀態觀測器的飛輪故障檢測與恢復［J］.北京航空航天大學學報，2008，34(11):1272－1275.JIN Lei，XU Shijie.Extendted state observer-based fault detection and recovery for flywheels［J］.Journal of Beijing University of Aeronautics and Astronautics，2008，34(11):1272 －1275.

［4］LI Zhongqi，MA Liying，KHORASANI Khashayar.Fault detection in reaction wheel of a satellite using observer-based dynamic neural networks［J］.Lecture Notes in Computer Science，3498(3):584－590.

［5］趙石磊，張迎春.SVM回歸估計方法在衛星故障診斷中的應用［J］.電機與控制學報，2008，12(4):483－486.ZHAO Shilei，ZHANG Yingchun.Application of SVM regression to fault diagnosis for satellite［J］.Electric Machines and Control，2008，12(4):483 －486.

［6］王劍非，姜斌，冒澤慧.基于LSSVM的衛星姿態控制系統故障診斷［J］.控制工程，2008，15(3):334－346.WANG Jianfei，JIANG Bin，MAO Zehui.LSSVM based fault diagnosis for satellite attitude control systems［J］.Control Engineering of China，2008，15(3):334 －346.

［7］HENRY D.Fault diagnosis of microscope satellite thrusters using H∞/H－filters［J］.Journal of guidance，control，and dynamics，2008，31(3):699－711.

［8］VALDES A，KHORASANI K.A pulsed plasma thruster fault detection and isolation strategy for formation flying of satellites［J］.Applied Soft Computing Journal，2010，10(3):746 －758.

［9］PIRMORADI F N，SASSANI F，DE SILVA C W.Fault detection and diagnosis in a spacecraft attitude determination system［J］.Acta Astronautica，2009，65(5 －6):710 －729.

［10］TIPPING Michael E.Bayesian inference:an introduction to principles and practice in machine learning［J］.Advanced lectures on machine learning，2006，3176:1－19.

［11］劉芳.基于小波分析和相關向量機的非線性徑流預報模型研究［D］.武漢:華中科技大學控制科學與工程系，2007.

［12］TIPPING Michael E.Sparse bayesian learning and the relevance vector machine［J］.Journal of Machine Learning Reaserch，2001，1:211 －244.

［13］LEI Liangyu，ZHANG Qing.Relevance vector machine based bearing fault diagnosis［C］//2006 International Conference on Machine Learning and Cybernetics，August 13 － 16，2006，Dalian，China.2006:3492 －3496.

［14］刑琰，魏春嶺.基于四元數估計角速率的陀螺故障定位［J］.宇航學報，2003，24(4):410－413.XING Yan，WEI Chunling.Fault location of single redundant gyroscopes based on estimated angular rate using quaternion ［J］.Journal of Astronautics，2003，24(4):410 －413.