因子分析在醫療保險學生成績綜合評價中的應用

李 慧 菏澤醫學專科學校醫療保險教研室,山東省菏澤市 274100

醫療保險專業是為適應當今社會對醫療保險人才的需要而設定的,該專業的學生應掌握醫療保險的基本理論和知識。為了更好的了解學生的綜合情況,需對學生多方面進行考核。學習成績無疑是考核中的重要一項內容。利用平均分對學生成績進行排名,并以此來對學生做綜合評價過于片面和籠統,無法顯示出學生在各學科間的優劣勢。作為一名大學生,在大學中需要學習的課程非常多,也就是說要想對這名學生的成績做一個評價,要考慮的課程是非常多的,并且一名學生各學科之間并不獨立,都存在著一定的相關性。若用全部的課程來做研究將使得我們的分析變得很復雜,反而不能清晰的的揭示出影響學生成績的主要原因。類似的問題在生活的其他方面同樣存在,比如經濟領域、社會領域和技術領域。因子分析能很好的解決這個問題。

因子分析起源于20世紀初,早期主要用于心理學和教育學方面的研究,《對智力測驗得分進行的統計分析》是早期的代表文章。因子分析是主成分分析的推廣和發展,也是多元統計中處理降維的一種方法。它通過研究眾多變量間的內部依賴關系來觀察數據中基本結構,并用少數幾個變量來表示原數據的基本結構。這些變量能反映原來眾多變量的主要的信息。將因子分析應用到學生成績的綜合評價中,避免了很多主觀因素的影響,使得分析結果更具有參考價值。

1 因子分析的基本原理

設有樣本容量為n的p個變量,因子分析是通過變換,將原 p個變量分別表示為k(k≤p)個公共因子和一個特殊因子的線性加權和,即;x1=a11F2+a12F2+…+a1mFk+ε1; x2=a21F2+a22F2+…+a2mFk+ε2;…;xp=ap1F1+ap2F2+…+apmFk+εp。其中,x1,x2,…,xp為 p個原變量,是均值為零,標準差為1的標準變量;F1,F2,…,Fk為k個公共因子變量,αij表示第i個原變量在第j個公共因子變量上負荷ε1,ε2…,εP,為特殊因子。

在因子分析中,存在兩個大問題,一是因子變量的構造,二是因變量的命名。具體來說,因子分析有以下幾個步驟。(1)檢驗原有的變量是否適合做因子分析。只有原變量間存在相關性才可以做因子分析,否則無法從中綜合出能反映變量共同特性的公共因子。常用的方法有巴特利特球形檢驗、反像相關矩陣檢驗和KMO檢驗。(2)構造因子。公共因子及其個數的確定方法是多種多樣的,如主成分分析法、主軸因子法、極大似然法和最小二乘法等。其中主成分分析法是較常用的方法之一。主成分分析法是對原相關變量進行線性變換,是指轉換成為另外一組相對獨立的變量,這一組變量稱為主成分。轉換得到的每一主成分可以代表或解釋一部分原變量的變化,選擇主成分時一般要使其能夠解釋變量累加到80%以上。(3)對公共因子變量進行解釋命名。建立了因子分析模型,得出了公共因子,但這些公共因子的含義模糊不清,不利于做實際的背景解釋。為了使每個公共因子有意義,首先做因子旋轉。因子旋轉是通過坐標變換使每個原始變量在盡可能少的因子之間有密切的關系。因子旋轉后可根據數據的實際情況給公共因子命名。(4)計算因子得分。

2 醫療保險專業學生成績的因子分析

對某校2008級醫療保險專業26名學生的成績做因子分析。選取他們的21們課程:藥理學、醫療保險、醫學倫理學、診斷學、生物化學、思想品德、衛生法學、計算機、解剖生理、經濟法學、臨床醫學、社會主義理論、人身保險、社會保險、保險法學、保險學、保險營銷、病理學、大學英語、高等數學和管理學原理作為變量,分別表示為 x1,x2…,x21。這26名學生的21門課程的成績構成26×21的矩陣,作為因子分析的原始數據。

利用SPSS16.0做因子分析。按Analyze→DataReduction→Factor順序單擊菜單,打開FactorAnalysis對話框,依次設置好Descriptives對話框、Extraction對話框、Rotation對話框、FactorScores對話框和Options對話框后,單擊ok按鈕即可。那么SPSS輸出的統計結果如下。

(1)對變量做 KMO檢驗和巴特利特球形檢驗,檢驗結果見表1。KMO檢驗值0.696＞0.5,巴特利特球形檢驗的卡方統計值571.475(P＜0.001),檢驗結果表明該數據適合做因子分析。(2)對數據做標準化處理后,選用主成分分析法做因子分析。得到公共因子的特征值和累計方差貢獻率,見表2。當取6個主成分時,累計的信息量達到了85.135% (＞80%),可以認為已能夠反映原數據的信息,因此,筆者把公共因子個數定為6。(3)由因子載荷矩陣(略)可以得到每個原始變量的因子表達式。為了給每個公共因子合理的解釋,利用方差極大旋轉法進行旋轉,得到旋轉后的因子載荷矩陣,見表3。根據各個主成分上課程因子載荷值的大小,分別命名為保險課因子、醫學基礎課因子、醫學專業課因子、公共基礎課因子、法律課因子和兩課因子。

表1 KMO檢驗和巴特利特球形檢驗

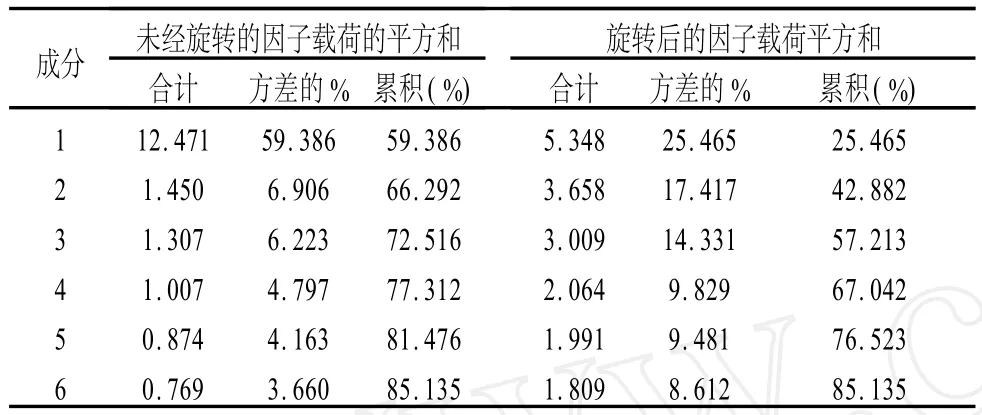
表2 解釋的方差及貢獻率

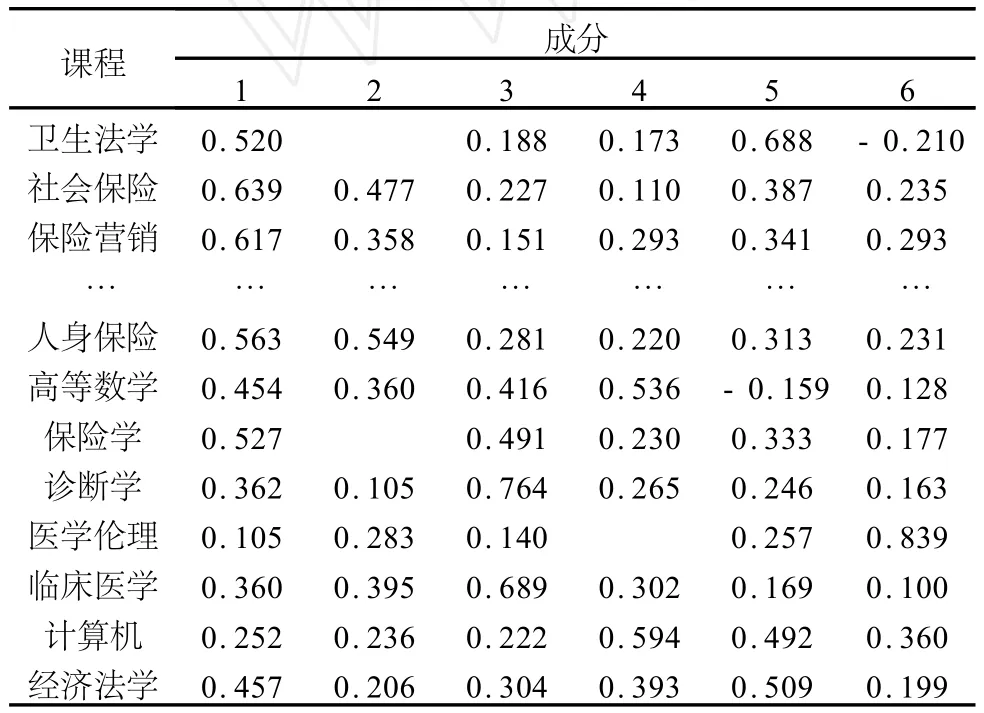
表3 旋轉后因子載荷矩陣

(4)通過回歸算法計算因子得分矩陣,見表4,因子得分函數為 F1=0.33x1+0.207x2+…+0.64x21,(5)根據旋轉后的特征值占總提取特征值的比例算得綜合得分為:Y= 0.299F1+0.205F2+0.168F3+0.125F4+0.116F5+ 0.101F6。根據公式算的學生的綜合評價如表4所示。因篇幅關系,只列出了前5名學生的評價表。

3 醫療保險專業學生成績的綜合評價

通過這一系列的分析,得出的學生綜合評價名次和原始成績算出來的名次有一定的差別但是不是特別大。從綜合評價表可以看出學生各學科的優劣。作為第1名的3號學生,在因子和具有很大的優勢,但偏科比較嚴重,因子排名非常靠后,但由于在和表現很突出,所以綜合排名仍然排在第1位。通過因子分析得出的綜合評價,可以更客觀反映學生的學習情況。學生學習比較薄弱的環節,可以有針對性的進行教學。為教師教學和學生學習提供參考依據。

[1] 張弛.師專數學專業學生知識能力結構的因子分析〔J〕.四川師范大學學報:自然科學版,1998,21(3):336-340.

[2] 張喜娟,丁釗鵬.因子分析在學生成績影響因素調查結果中的應用〔J〕.北京聯合大學學報(自然科學版),2010,24(1):77-81.

[3] 盧紋岱.SPSS統計分析〔M〕.第4版.北京:電子工業出版社, 2010.

[4] 唐功爽.基于SPSS的主成分分析與因子分析的辨析〔J〕.統計教育,2007,(2):12.