“研究性學習”實施一例

盧 勇

研究性課程旨在培養學生的創新精神和創造能力,它要求給學生提供研究的問題和背景,讓學生自主研究知識的發生、發展過程,因而具有研究性;從問題的提出,方案的設計和實施,到結論的得出,均由學生來做,因而具有自主性;它一般要通過調查、實驗、歸納猜想、推證結論、社會實踐等方式進行學習,因而具有開放性和實踐性。

目前,研究性學習已作為一門正式課程列入教學計劃,各校對研究性學習課程的開發方興未艾。本文以自己的教學實施為例,談談研究性課程的教學實施。

一、問題的提出

研究性課程學習最關鍵的環節是確定研究專題,而專題的確定有兩種模式:一是從學生生活和社會生活中選擇和確定專題;二是創設問題情景由課堂教學直接切入課題,課題內容是教學內容的延伸,后者應該是研究性課程開展的常用方法。

例如我在課堂研究函數圖像的性質時,先展示這樣一道題:

問題1設函數f(x)定義在實數集上,則函數f(1-x)與f(1+x)的圖像關于()

A.直線y=0對稱 B.直線x=0對稱

C.直線y=1對稱 D.直線x=1對稱

選什么呢?學生常常容易與下一題混淆而錯選D。不妨請學生再來看這樣一道題:

問題2設函數f(x)定義在實數集上,且滿足f(1-x)=f(1+x),則有f(x)的圖像關于()

A.直線y=0對稱 B.直線x=0對稱

C.直線y=1對稱 D.直線x=1對稱

問:這兩題一樣嗎?區別在哪里?如何解答?

學生們通過仔細比較,不難發現兩題不一樣,前者是兩函數f(1-x)與f(1+x)之間的對稱問題;后者則是函數f(x)自身的對稱問題。 此時有學生通過特例,如令f(x)=x2得出問題1的答案選B、問題2的答案選D。

再問:它們的一般形式各是什么?又有什么樣的一般結論呢?類似于它們的一般形式的問題還有哪些?如何解答?請同學們課后認真加以研究和探索。

二、問題的探討

研究性專題確定以后,學生在解決了以上兩個具體問題基礎上,自己動手收集資料,自己動手實驗、歸納、探索、總結,學生之間互相討論、交流后發現:

以上兩題的一般形式分別為“f(a-x)與f(a+x)”和“f(a+x)=f(a-x)”,并得到如下一些結論:

結論1:定義在實數集R上的函數f(x),

(1)若滿足f(a+x)=f(a-x),則有f(x)圖像關于直線x=a對稱;

(2)若滿足f(x-a)=f(a-x),則有f(x)圖像關于直線x=0(y軸)對稱;

(3)若滿足f(x-a)=f(x+a),則有f(x)為周期T=2|a|的周期函數。

理由:(1)以a>0為例,∵f(a+x)=f(a-x)∴f(a+x)為偶函數,其圖像關于y軸對稱,再將圖像向右平移a個單位得f(x)的圖像,即f(x)的圖像關于直線x=a對稱,其等價形式為“f(x)=f(2a-x)”。

(2)f(x-a)=f(a-x)即f(t)=f(-t),從而f(x)為偶函數,其圖像關于y軸對稱。

(3)條件可轉化為f(x)=f(x+2a),符合周期函數的定義,f(x)為周期函數T=2|a|。

教師啟發:觀察以上的結論,你又能發現什么規律嗎?對(1)你能作更一般的推廣嗎?

此時,學生不難發現出這樣的特征:若條件中等式兩邊括號里x前系數相反,則f(x)的圖像為軸對稱(如(1)、(2));若x前系數相同,f(x)為周期函數(如(3))。同時,對(1)推廣得更一般的結論:

結論2:定義在實數集R上的函數f(x),若滿足f(a+x)=f(b-x),則有f(x)圖像關于直線x=2/(a+b)對稱。

理由:f(a+x)=f(b-x)等價于f(2/(a+b)+x)=f(2/(a+b)-x).

不難發現,結論1中(2)也是結論2的特例。

學生通過啟發、思考、 討論,交流,又出現新的研究成果,學生為一種結論的得出而欣喜,又進一步激發他們探究的欲望,導致新成果不斷涌現。

結論 1': 定義在實數集R上的函數f(x),

(1)若滿足f(a+x)=-f(a-x), 則有f(x)圖像關于點(a,0)對稱;

(2)若滿足f(x-a)=-f(a-x), 則有f(x)圖像關于點(0,0)對稱;

(3)若滿足f(x-a)=-f(x+a),則有f(x)為周期T=4|a|的周期性函數。

理由:以a>0為例,

(1)式中可記f(a+x)=φ(x),條件為φ(x)= -φ(-x),得φ(x)即f(a+x)為奇函數,其圖像關于原點對稱。而f(x)的圖像可由φ(x)的圖像向右移a個單位而得,從而得f(x)圖像關于點(a,0)對稱。

(2)式中等價于f(-t)=-f(t)知f(x)為奇函數,其圖像關于原點對稱。

(3)式中可令x-a=t,從而得f(t+2a)=-f(t),所以f(t+4a)=-f(t+2a)=-[-f(t)]=f(t),即f(t+4a)=f(t),知f(x)為周期函數,T=4a。

結論2':定義在實數集R上的函數f(x),若滿足f(a+x)=-f(b-x), 則有f(x)圖像關于點(2/(a+b),0) 對稱。

教師進一步啟發:比較結論 1和結論1',或結論2和結論2',你又發現什么規律?

學生容易得出:區分“軸對稱”與“中心對稱”的標準是等式兩邊是否相差負號。

在以上以某函數自身為研究對象的研究性學習過程中,應該相信:學生在獲取知識的同時,也基本掌握了這類問題的研究方法,再研究兩個函數之間的關系就輕而易舉了。

結論3:若f(x)定義在實數集R上,則

(1)f(a-x)與f(a+x)的圖像關于直線x=0對稱,

(2)f(x-a)與f(a-x)的圖像關于直線x=a對稱,

(3)f(x-a)的圖像左(右)平移2|a|個單位可得f(x+a)的圖像。

理由(1)中由于函數f(a+x)已不是f(x),而是由f(u)與u=a+x復合而成的函數,可記為g(x),即f(a+x)=g(x),則f(a-x)=g(-x)。顯然,g(x)與g(-x)圖像關于y軸對稱,即f(a-x)與f(a+x)的圖像關于y軸對稱。

(2)中以a>0為例:

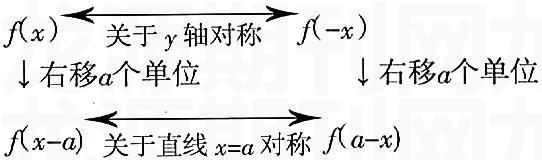
(3)以a>0為例,將f(x-a)的圖像左移2a個單位可得f(x+a)的圖像。

結論4:若f(x)定義在實數集R上,則函數f(a+x)與函數f(b-x)的圖像關于直線x=2/(b-a)對稱。

理由:以a>0,b>0為例,f(x)與f(-x)圖像關于y軸對稱,而f(a+x)的圖像可由f(x)的圖像向左平移a個單位而得,函數f[-(x-b)]的圖像可由f(-x)的圖像向右平移b個單位而得,因此函數f(a+x)與函數f(b-x)的圖像關于直線x=x=2/(b-a)對稱。

結論3':若f(x)定義在實數集R上,則

(1)f(a+x)與-f(a-x)的圖像關于點(0,0)對稱,

(2)f(x-a)與-f(a-x)的圖像關于(a,0)對稱,

(3)f(x+a)的圖像需作左(右)平移和關于x軸的對稱交換,可得-f(x-a)的圖像。

理由略。

結論4':若f(x)定義在實數集R上,則函數f(a+x)與函數-f(b-x)的圖像關于點(x=2/(b-a),0)對稱。

理由略。

最后,提請學生對以上內容加以整理、概括、提煉。學生歸納如下:

(一)解答此類問題的步驟:首先,要分清是一個函數自身的問題,還是兩個函數之間的問題;第二步,是對稱性問題,還是周期性問題,無論是一個函數自身還是兩個函數之間,只要一般形式中x前的符號相同,就是周期性問題,反之,就是對稱性問題。

(二)為區分各類情形,可歸納成下表:

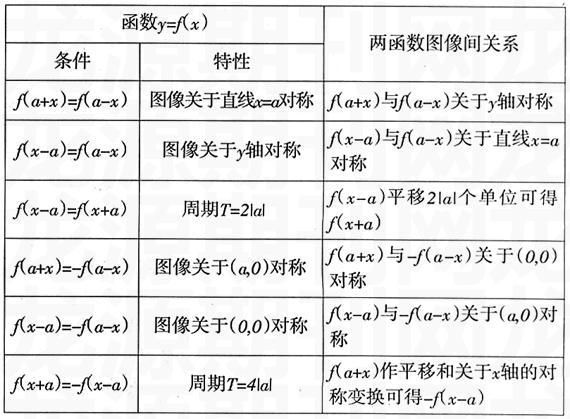
事實證明:在研究性學習中,學生的學習完全是自主的、開放的,開設研究性課程是實現創新教育的一條必由之路。