單元整體教學背景下初中數學校本單元作業設計

摘" 要：筆者以八年級下冊《平行四邊形》為例，介紹其單元學習概覽，包括知識、技能和情感態度目標及知識點回顧.設計鞏固型、實踐型和拓展型作業，旨在全面加深學生對平行四邊形及其性質的理解，提升解題技能和實際應用能力.通過多樣化的作業設計和評價標準，促進學生全面發展.

關鍵詞：單元整體教學；初中數學；作業設計；平行四邊形

中圖分類號：G632""" 文獻標識碼：A""" 文章編號：1008-0333（2025）05-0027-03

收稿日期：2024-11-15

作者簡介：宋顯梅，本科，一級教師，從事初中數學教學研究.

基金項目：福建省教育科學“十四五”規劃2023年度“協同創新”專項課題“單元整體教學視域下初中數學校本作業設計與實施研究”（立項批準號：Fjxczx23-410）.

隨著新課程改革的不斷深入，單元整體教學倍受初中數學教師青睞.筆者圍繞八年級下冊《平行四邊形》單元教學，詳細闡述學習目標、知識點回顧及作業設計.通過校本單元作業全面加深學生對平行四邊形性質的理解.借助多樣化作業與公正評價標準，旨在促進學生邏輯思維、創新能力和實際應用能力的全面發展，為終身學習打下堅實基礎.

1" “平行四邊形”單元學習概覽

1.1" 單元學習目標

知識目標：在《平行四邊形》單元教學中，學生必須掌握核心概念與基本性質.學生需理解平行四邊形的定義，即兩組對邊平行的四邊形，并熟悉其基本性質，如對邊相等、對角相等、鄰角互補及對角線互相平分.同時，學生應掌握判定定理，如通過“一組對邊平行且相等”判定平行四邊形.這些知識能夠為學生后續學習矩形、菱形、正方形等特殊平行四邊形奠定基礎，并提供解決實際問題的理論支持.

技能目標：在“平行四邊形”單元教學中，技能目標側重提升學生運用平行四邊形的性質和判定解決問題的能力，包括培養學生通過觀察和分析圖形，運用邏輯推理和空間想象證明幾何命題的技能.學生將學習如何在給定條件下，有效判定一個四邊形是否為平行四邊形，并能夠利用平行四邊形的性質解決相關的幾何問題，如計算平行四邊形的面積、周長或找出圖形的對稱性.

情感態度目標：在《平行四邊形》單元教學中，情感態度目標致力于激發學生對數學學習的興趣，培養他們持之以恒的學習態度和積極的學習習慣.此外，在小組討論和合作解題的過程中，學生有機會交流思想、分享解題策略，這不僅有助于提升個人的解題能力，還能促進學生之間相互理解和合作交流，建立和諧的人際關系.

1.2" 知識點回顧

平行四邊形的定義和性質：平行四邊形是一種特殊的四邊形，其兩組對邊分別平行.學生需要掌握平行四邊形的基本性質，包括對邊平行且相等、對角相等、鄰角互補以及對角線互相平分等.這些性質不僅有助于學生識別和判定平行四邊形，還是解決相關幾何問題的基礎.

平行四邊形的判定定理：判定一個四邊形是否為平行四邊形，可以依據一些特定的條件.這些判定定理包括：如果一個四邊形的兩組對邊分別平行，那么這個四邊形是平行四邊形；如果一個四邊形的兩組對邊分別相等，那么這個四邊形是平行四邊形；如果一個四邊形的一組對邊既平行且相等，那么這個四邊形是平行四邊形等.學生通過學習這些定理，能夠更準確地在各種情境下判定平行四邊形.

平行四邊形的特殊類型：特殊的平行四邊形包括矩形、菱形和正方形.矩形是四個角均為直角的平行四邊形，對邊平行且相等，具有對稱性；菱形則是一組鄰近相等的平行四邊形，邊長相等但角度不固定；正方形兼具矩形和菱形的特性，四個角均為直角且四邊相等.了解這些特殊平行四邊形及其性質，能加深學生對平行四邊形概念的理解，培養他們識別和區分幾何形狀的能力，進而更好地理解幾何圖形的多樣性和復雜性.

2" “平行四邊形”單元作業設計

2.1" 鞏固型作業設計

為了鞏固學生對《平行四邊形》單元內容的理解和掌握，以下設計三個鞏固型作業，旨在通過不同的角度和方法，加深學生對平行四邊形性質的認識，并提高他們的解題技能.

作業1" 選擇題

設計一系列選擇題，涵蓋平行四邊形的基本性質、判定定理以及特殊平行四邊形的識別.

例1" 如果一個四邊形的對角線互相平分，那么這個四邊形一定是（" ）.

A.矩形" B.菱形" C.平行四邊形" D.正方形

作業2" 填空題

給定平行四邊形，讓學生根據圖形的性質填寫空缺部分，如對邊長度、角度等，加深學生對平行四邊形性質的理解.

例2" 在平行四邊形ABCD中，如果∠A=70°，那么∠C=°.

作業3" 實際應用題

提出一些與實際生活相關的問題，讓學生應用平行四邊形的知識解決問題，如計算地圖上表示的土地面積，或設計具有特定幾何屬性的圖案等.

例3" 設計一個花園，使其四周的圍墻形成一個菱形，邊長為20米，有一個角為60°，求花園的面積.

設計理由及動機：這些作業的設計旨在通過多樣化的練習形式，從不同維度加強學生對平行四邊形知識點的理解和應用能力.選擇題和填空題可以幫助學生快速回顧和鞏固平行四邊形的基本概念和性質；實際應用題則將理論知識與實際情境相結合，有助于提高學生解決實際問題的能力［1］.

2.2" 實踐型作業設計

實踐型作業旨在將學生從課堂理論學習引向實際操作和實踐探索，通過具體的動手實踐活動，加深對平行四邊形知識的理解和應用.

作業1" 制作幾何模型

使用硬紙板制作不同類型的平行四邊形模型，如矩形、菱形、正方形，并標注出其對邊、對角、對角線等重要幾何特征.

此活動要求學生不僅準確理解平行四邊形的性質，還需動手實踐.通過制作過程，深化學生對幾何形狀的理解，提升學生的幾何素養.

作業2" 平行四邊形獵尋

組織一次“平行四邊形獵尋”活動，讓學生在校園內或家庭環境中尋找各種平行四邊形的實例.

學生需要說明每個實例如何體現平行四邊形的性質.此任務鼓勵學生觀察生活中的幾何圖形，在實踐中學習和發現數學之美.

作業3" 心何推理

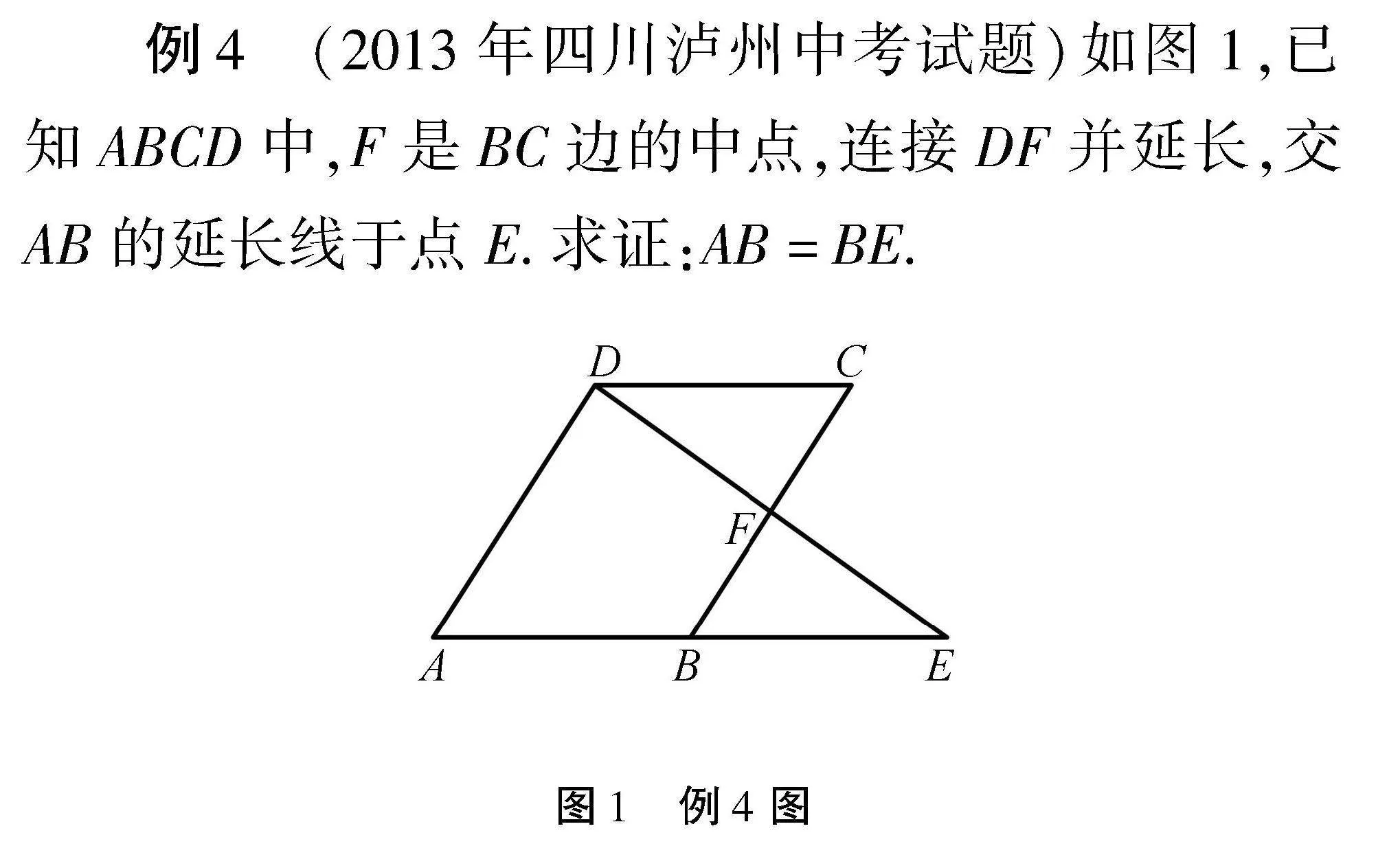
例4" （2013年四川瀘州中考試題）如圖1，已知ABCD中，F是BC邊的中點，連接DF并延長，交AB的延長線于點E．求證：AB=BE．

設計理由及動機：首先，通過動手制作和實際探索活動，學生可以將抽象的數學知識轉化為具體和直觀的理解，使學習過程更加生動有趣；其次，實踐型作業能夠激發學生的探索興趣和創新思維，鼓勵他們主動學習和應用知識解決問題；最后，這些作業強調學習與實際生活的聯系，能夠幫助學生認識數學知識的實用價值，增強學習的目的性和實用性.

2.3" 拓展型作業設計

拓展型作業旨在推動學生超越基礎知識，探索更深層次的數學知識，激發創新思維和解決復雜問題的能力，提升學生的數學核心素養.

作業1" 幾何變換探究

探究平行四邊形在平移、旋轉、對稱等不同幾何變換下的性質變化.

學生需要選擇一個平行四邊形，進行系列的幾何變換，并記錄每次變換后的性質變化.通過此活動，學生不僅能夠深化對平行四邊形性質的理解，還能掌握幾何變換的基本概念和應用.

作業2" 探索平行四邊形的性質

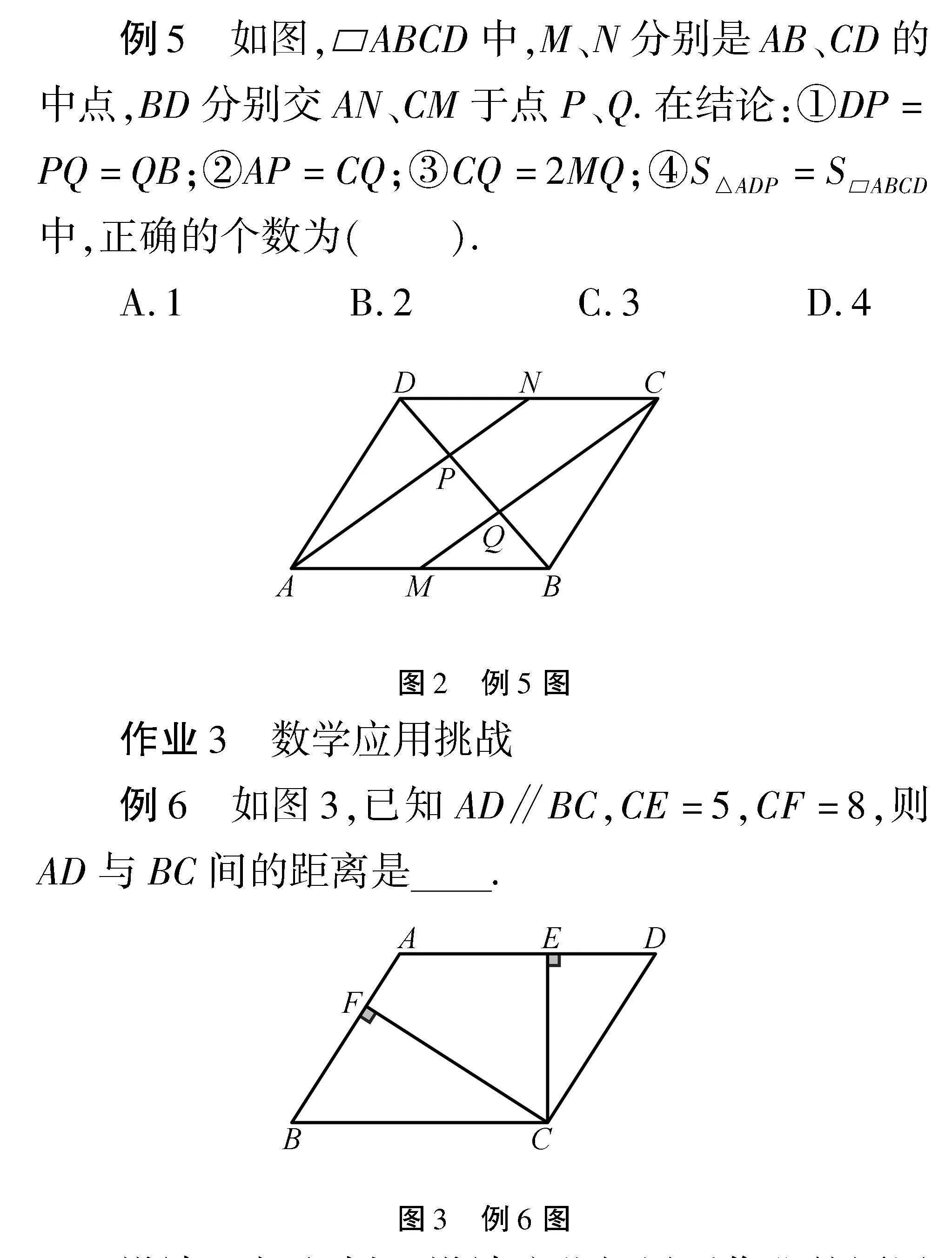
例5" 如圖，ABCD中，M、N分別是AB、CD的中點，BD分別交AN、CM于點P、Q.在結論：①DP=PQ=QB；②AP=CQ；③CQ=2MQ；④S△ADP=SABCD中，正確的個數為（" ）.

A.1""" B.2""" C.3""" D.4

作業3" 數學應用挑戰

例6" 如圖3，已知AD∥BC，CE=5，CF=8，則AD與BC間的距離是.

設計理由及動機：設計這些拓展型作業的原因和動機在于促進學生在掌握基礎知識的基礎上，進一步拓寬知識視野，提高抽象思維和創新能力.

3" 作業評價標準

在設計《平行四邊形》單元作業時，建立公正、全面的評價標準至關重要.首先，評估學生理解和應用平行四邊形及其特殊形狀定義、性質的能力及這些知識在解決問題中的應用；其次，評價學生解題過程的邏輯清晰度和步驟完整性，特別關注證明題的充分性和合理性；最后，考查學生的情感態度和參與度，如作業的認真度和學習積極性.這些標準能全面、公正地評估學生學習成果，激勵他們持續進步，培養創新意識和解決問題能力，旨在促進學生全面發展，為未來的學習和職業生涯奠定堅實基礎.

4" 教學反思

在八年級下冊《平行四邊形》單元的學習中，筆者設計了鞏固型、實踐型和拓展型作業，旨在為學生構建一個全面的學習平臺.這些作業精心挑選，旨在加深學生對平行四邊形及其性質的理解，并通過實踐活動和創新挑戰激發學生的積極性和能力.鞏固型作業能夠使學生掌握平行四邊形的識別和性質應用，增強邏輯推理和空間想象能力；實踐型作業讓學生看到數學在現實世界中的應用，能夠增強學生的學習興趣；拓展型作業能夠拓寬學生視野，激發學生的創造力，并培養解決問題的多樣化思維方式.這種綜合設計不僅能夠提高學生對知識的掌握程度，更能促進他們批判性和創新性思維的發展.

5" 結束語

經過對《平行四邊形》單元的深入學習，學生不僅掌握了核心概念和基本性質，而且通過多樣化的作業設計提升了解決問題的能力.這種綜合教學方法能夠激發學生的積極性和創造力，為他們未來的學習奠定堅實的基礎.

參考文獻：［1］ 李慧青.初中數學教師單元作業設計現狀調查研究［D］.石家莊：河北師范大學，2022.

［責任編輯：李慧嬌］