基于GeoGebra的中職數學探究性教學的實踐研究

【摘要】文章從GeoGebra軟件介紹、中職數學探究性教學的必要性、GeoGebra為進行數學探究性教學提供便利、準備自主探究教學的教室、基于GeoGebra的中職數學性探究教學的實踐五方面闡述基于GeoGebra的中職數學探究性教學的實踐研究。

【關鍵詞】GeoGebra；中職數學；探究性教學；對數函數

隨著時代的發展與科技的進步，利用信息技術輔助數學教學的手段和案例是時代的必然趨勢。GeoGebra作為現代化的教學工具之一，它操作比較簡單，對于教師展示教學內容十分合適，并且能幫助學生進行自主探究，以及教師與學生之間的互動交流。GeoGebra以其免費動態、功能強大、易于操作等優點成為越來越多的教師輔助教學的有力工具。而探究性教學是以學生為中心，以教師為指導的教學方式。將GeoGebra用于中職數學探究性教學，能有效地融合二者優點，激發學生學習欲望，刺激學生的直觀感受，使枯燥乏味的數學課堂變得生動有趣，提高教學效率[1]。為此，結合具體的教學案例進行分析。

一、GeoGebra軟件介紹

GeoGebra軟件是美國佛羅里達州亞特蘭大的數學教授Markus Hohenwart于2002年設計開發的，是一款免費動態數學教學軟件[2]。它由兩部分組成的，即 “Geometry”＋“Algebra”，也就是形（幾何）和數（代數）的完美融合，凡是數形結合的東西都可以在GeoGebra中制作，并能動態的演示。

GeoGebra軟件主要有以下特點：免費軟件，資源共享。GeoGebra是基于Java程序編寫的，支持多平臺的應用，用戶可以在手機、電腦、瀏覽器上查閱或操作，為技術的交流和資源的共享提供了極大的便利。操作簡單，易于上手。GeoGebra界面豐富可以直接使用工具欄，也可以輸入命令（中英文指令都支持），輸入中文命令時，自帶聯想補全功能，顯示與輸入文字接近的命令。功能強大，動態演示。GeoGebra將幾何作圖、代數運算和數據處理等功能融于一體兼具函數與集合、概率與統計、工作表與圖表、向量與矩陣計算等功能[1]，幾乎可以完成從啟蒙教育到大學教育中的所有的數學教學，也可應用物理、化學等多種學科，對于56種語言都能夠提供支持。GeoGebra作圖實現了動態化，且具備三維功能，輸入命令即可快捷地構建出圖形，還可動態演示圖像的生成和展開過程，真正做到“所見即所得”。

二、中職數學探究性教學的必要性

中等職業學校數學課程是中等職業學校各專業學生必修的公共基礎課程，承載著落實立德樹人根本任務、發展素質教育的功能，具有基礎性、發展性、應用性和職業性等特點。有效的數學學習活動不能單純依賴模仿和記憶，動手實踐、自主探究與合作交流是學生學習數學的重要方法。探究性學習已經成為基礎課程教學的基本要素。目前，中職數學課堂學習方式較為單一、被動，缺少自主探索合作學習的氛圍；教師對學生探究精神和實踐能力的培養有待提高[3]。《中職數學課程標準（2020年版）》強調學生要“積累一定的數學實踐經驗、增強創新意識”，學生的實踐經驗是在運用知識解決問題的實踐活動中積累發展的，學生的創新意識是在主動探索知識的過程中得到增強的，課堂教學應該是學生積累實踐經驗和增強創新意識的主陣地。因此，進行數學探究性教學的實踐意義重大。

三、GeoGebra為進行數學探究性教學提供便利

動態變化和數形結合是數學兩種重要思想，近年來教學中常用幾何畫板來輔助教學，但是幾何畫板的基本原理是尺規作圖，重點用于輔助平面幾何教學，在某些內容的教學上有一定的局限性，比如圓錐曲線和立體幾何中的圖形就很難用幾何畫板作出，另外對一些稍微復雜的圖形，作圖過程極其復雜，不利于學生理解。而GeoGebra可以很好地解決這個問題，它所獨具的動態變化和豐富的作圖功能為培養學生的數學核心素養創造了條件，也為在教學過程中合理運用信息技術促進數學探究性活動的開展提供了極大的便利。

四、準備自主探究性教學的教室

如果在普通的多媒體教室使用GeoGebra教學，可配備25或50臺ipad（每臺都安裝上GeoGebra）保證每兩位或一位學生一臺；也可以在計算機多媒體理實一體化實訓室進行教學，同樣50臺計算機上都安裝上GeoGebra，只有這樣學生才可以自主實踐、自主探究。以上是利用GeoGebra在中職數學教學中培養學生自主探究學習能力的硬性要求。

五、基于GeoGebra的中職數學探究性教學的實踐

對數函數是中職數學學習的比較困難的一個知識點，畫圖不夠精確與方便，缺乏空間想象力等，很多學生都在這一部分學得非常吃力，甚至失去了對數學學習的信心，所以如何把對數函數這一部分教得通俗易懂是一件很有意義的事情。本文以典型案例“對數函數”為例，教師首先創設教學情境，激發學生的探究興趣，然后根據教學內容，設計探究任務，驅動學生自主探究，動手操作，從而由淺入深地理解所學，提高課堂學習效率[4]。

教學過程：創設情境

情境：已知某種細胞分裂時，由１個分裂成２個，２個分裂成４個，4個分裂成8個……得到的細胞個數y是分裂次數x的函數，這個函數表示為y=2x，x∈N*.反過來，如果我們知道細胞個數，如何得到細胞分裂的次數呢？進一步，分裂次數x是細胞個數y的函數嗎？

教師：引導學生聯系實際進行思考。

學生：探究題目，發現規律，寫出函數解析式。

由于細胞個數y是分裂次數x的函數，這個函數表示為y=2x，x∈N*。由對數的定義可知，分裂次數x與細胞個數y之間的關系可以寫為x=log2y。

因為我們習慣用x表示自變量，y表示函數，因此將這個函數寫成y=log2x。

引導學生觀察函數的特征：含有對數符號，底數是常數，真數是變量，從而得出對數函數的定義：函數y=logaxa＞0且a≠1叫作對數函數，由“零和負數沒有對數”可知，對數函數的定義域為（0，+∞）。

引導探究

教師：研究基本初等函數的性質和步驟？

學生：①畫出函數的圖像；②研究函數的性質。

教師：畫對數函數的圖像是否需要分類？

學生：按a＞1和0＜a＜1分類討論。

教師：觀察圖像主要看哪些特征？

學生：從圖像的形狀、位置、單調性、奇偶性、定點等角度去觀察分析。

教師：接下來從不同維度共同探究對數函數的圖像和性質。

實踐探究

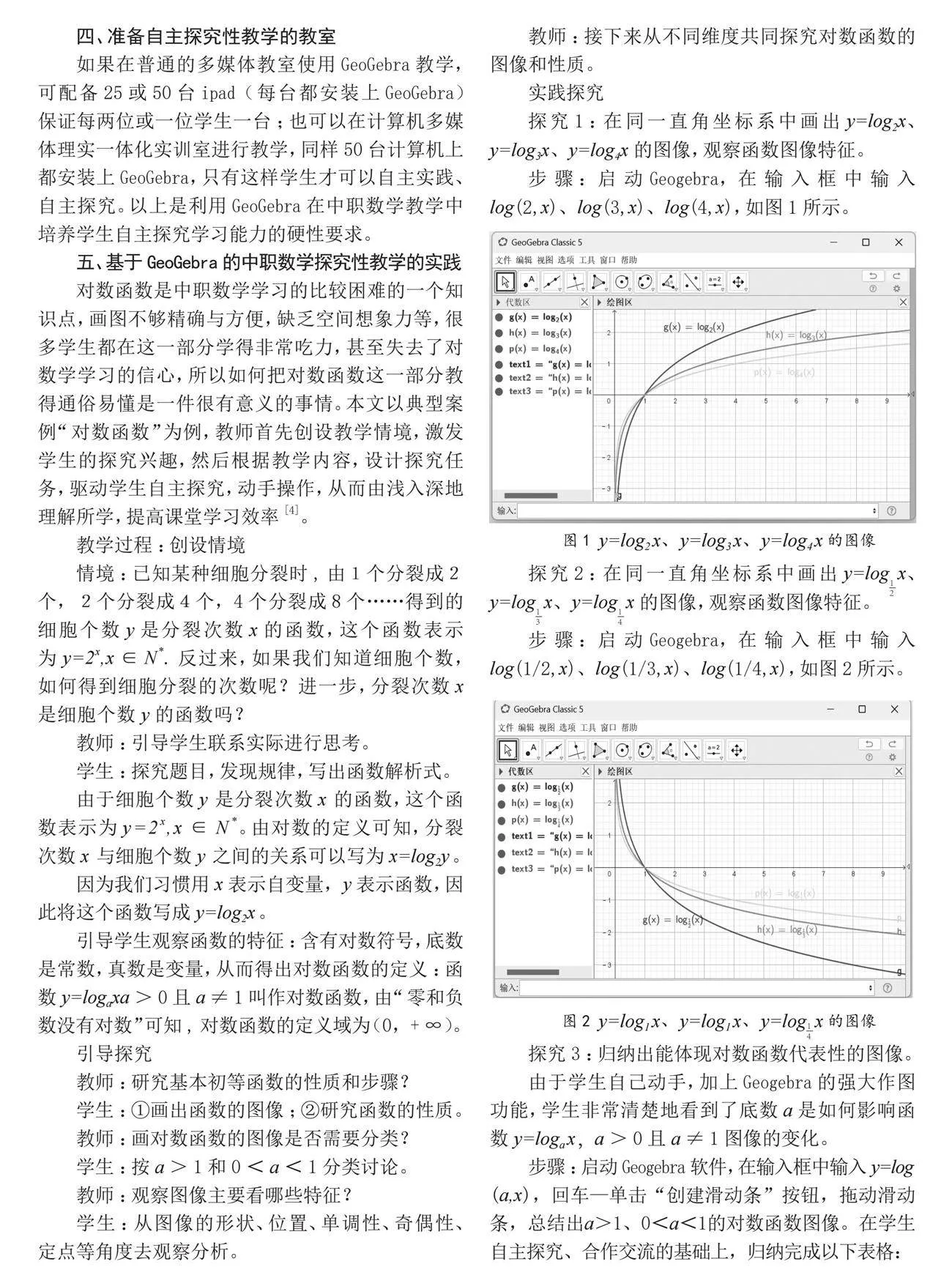
探究1：在同一直角坐標系中畫出y=log2x、y=log3x、y=log4x的圖像，觀察函數圖像特征。

步驟：啟動Geogebra，在輸入框中輸入log（2，x）、log（3，x）、log（4，x），如圖1所示。

圖1 y=log2x、y=log3x、y=log4x的圖像

探究2：在同一直角坐標系中畫出y=logx、y=logx、y=logx的圖像，觀察函數圖像特征。

步驟：啟動Geogebra，在輸入框中輸入log（1/2，x）、log（1/3，x）、log（1/4，x），如圖2所示。

圖2 y=log1x、y=log1x、y=logx的圖像

探究3：歸納出能體現對數函數代表性的圖像。

由于學生自己動手，加上Geogebra的強大作圖功能，學生非常清楚地看到了底數a是如何影響函數y=logax，a＞0且a≠1圖像的變化。

步驟：啟動Geogebra軟件，在輸入框中輸入y=log

（a，x），回車—單擊“創建滑動條”按鈕，拖動滑動條，總結出a＞1、0＜a＜1的對數函數圖像。在學生自主探究、合作交流的基礎上，歸納完成以下表格：

（1）比較下列各題中兩值的大小。

log30.7 log30.8； log0.234 log0.235；

log0.23 log34；

（2）求下列函數的定義域：

①y=log2（x?5）； ②；

在整個教學過程中，學生通過在GeoGebra作圖切切實實證明了對數函數的圖像，通過動態演示感受到了底數對于函數圖像的影響，通過自主探究、自主學習，觀察歸納整理得出對數函數的性質，并通過學以致用加深了知識的理解與運用。計算機技術的運用不僅增強了學生學習數學的積極性，又提高了學生的數學素養和信息計算素養。

綜上所述，借助GeoGebra開展中職數學探究性教學，不僅使原本抽象單調的課堂變得活躍豐富、有趣，也使抽象的數學概念變得直觀、生動，大幅提升了課堂效率、教學質量和學生學習數學的興趣；希望本文能夠為推進中職數學探究性教學課程改革提供一個路徑，也為中職數學教師借助GeoGebra改進教學實踐提供一些參考。

【參考文獻】

[1]朱亮衛.基于GeoGebra的高中數學探究式教學研究[D].漢中：陜西理工大學，2020：1.

[2]錢文濤，趙軍.Geogebra軟件讓數學教學如虎添翼[J].中國教育技術裝備，2014（02）.

[3]蔡進.基于GeoGebra的中職數學探究教學的實踐探索[D].揚州：揚州大學，2019：1.

[4]樊輝榮.高中數學探究性教學的實施策略[J].新課程，2020（33）.

【項目課題】珠海市教育科研2023年度市規劃課題“基于GeoGebra的中職數學探究性教學的實踐研究”（課題編號：2023ZHGHKT005）階段性成果之一。