模型觀念：內涵、培養路徑及教學示例

【摘 要】培養學生的模型觀念是義務教育階段數學教育的重要目標之一。基于對模型觀念的內涵理解，教師可以從以下三個途徑優化應用類問題教學：緊貼生活，呈現實際問題的原生性；合作探究，經歷數學建模的過程性；分步實施，體悟數學建模的階段性。

【關鍵詞】初中數學；模型觀念；數學學科德育；數學建模能力；應用類問題

【中圖分類號】G633.6 【文獻標志碼】A 【文章編號】1005-6009（2024）39-0046-05

【作者簡介】孫凱，江蘇省蘇州市陽山實驗初級中學校（江蘇蘇州，215151）教師，高級教師。

數學是一門邏輯性很強的基礎科學，也是一種應用廣泛的技術。數學應用性的實現途徑主要是數學建模。近年來，國際數學教育界越來越重視數學建模，都將培養學生的數學建模能力作為重要內容寫入數學課程標準。［1］我國數學教育也尤為注重學生數學建模能力的培養。根據學生的心理特征和認知水平，新的數學課程標準在小學、初中、高中三個學段分別提出了模型意識、模型觀念和數學建模的課程目標和教學要求。

為了凸顯數學與現實世界的聯系，蘇科版初中數學教材中設置了大量與生活實際緊密聯系的問題情境（尤其在數學概念和數學知識應用的內容部分），但這些問題情境的教學目標單一，問題的數學化程度高，更側重于建構標準數學模型求解問題，有利于培養學生模型觀念的再現水平，在模型觀念的聯系和反思水平上卻表現不足。在實際教學中，我們發現這些問題情境具有簡化性、封閉性、確定性等特征，與綜合性、開放性、不確定性的數學建模問題相比，這樣的問題情境難以驅動學生完整經歷數學建模活動過程，培養初中生模型觀念的效果不佳。

一、模型觀念的內涵

1.對模型觀念的理解

《義務教育數學課程標準（2022年版）》（以下簡稱“新課標”）明確提出，要培養初中生的模型觀念。模型觀念是指初中生在解決實際問題時，對建立數學模型，求解模型并驗證結果，最終闡釋實際問題的過程有清晰的認識。具體要求為，“對運用數學模型解決實際問題有清晰的認識，知道數學建模是數學與現實聯系的基本途徑，初步感知數學建模的基本過程，逐步建立模型觀念”［2］。

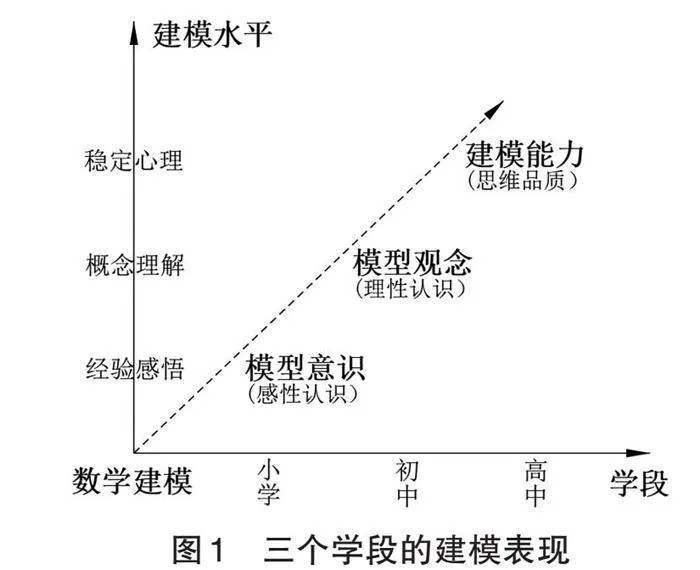
模型觀念是一種基于對數學概念的理解，逐步形成的對數學模型特征、問題與思考方式的理性認識；模型意識是一種數學學習經驗的積累，是學生在簡單數學建模活動中形成的感性認識；建模能力是一種穩定的心理特征，是學生經歷數學建模活動，在問題解決的過程中形成的數學能力和思維品質。［2］51小學、初中、高中階段學生的數學建模表現如圖1所示。相較于“數學建模的能力”而言，“模型觀念的認識”的要求稍微低一些，這與初中生數學知識和能力水平不高以及掌握的數學模型有限等因素相關。從模型觀念的“認識”的內容看，主要包括“運用數學模型”“解決實際問題”兩個方面；從“認識”的過程看，主要包括從實際問題中抽象出數學問題，用數學符號建立方程、不等式、函數、統計、概率等數學模型，求解模型獲得數學結果，討論結果的意義并闡釋問題。［3］模型觀念的功能體現在讓學生知道數學建模是聯系數學世界與現實世界的基本途徑，其意義在于在問題解決的過程中提高數學語言表達能力，感悟數學應用價值。

2.模型觀念與數學建模的關系

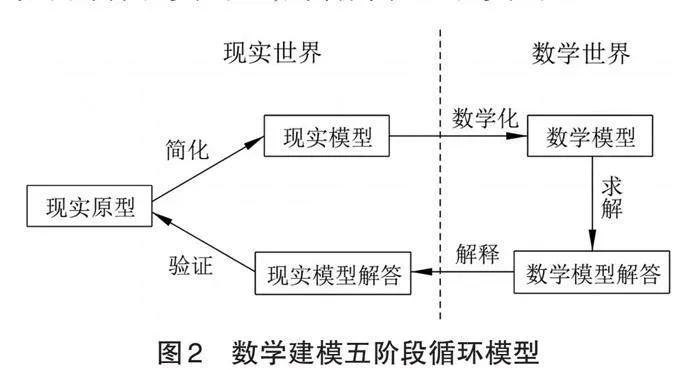
新課標給出了數學建模的基本過程。研究發現，模型觀念下的數學建模基本過程與《普通高中數學課程標準（2017年版2020年修訂》（以下簡稱“高中數學新課標”）中數學建模的過程基本一致，一般將其簡稱為數學建模五階段循環模型［4］（如圖2），具體包括：從現實原型簡化出現實模型（實際模型），從現實模型數學化形成數學模型（數學形式），求解數學模型獲得結果，用數學結果解釋現實問題，解答并驗證現實問題。

模型觀念是對數學建模的一種認識，學生的模型觀念必然形成于數學建模活動，因此，開展數學建模活動是培養學生模型觀念的重要路徑。數學建模活動具有現實性、開放性、過程性、階段性等特征。數學建模的關鍵環節是“現實原型—實際模型—數學形式”這一子過程。［5］從這個維度看，蘇科版初中數學教材上提供的數學概念類問題情境和數學知識應用類問題情境非常適合開展數學建模活動，但這些問題情境削弱甚至缺失了數學建模的簡化環節、數學化環節，教師在教學時可根據教學需要對其進行改編和優化。

二、模型觀念的培養路徑

創設真實、合適的問題情境是培養模型觀念的基礎，經歷數學建模的基本過程是形成模型觀念的必經路徑。［6］初中代數的許多應用問題具備了數學建模活動的部分特點，有助于學生形成與發展模型觀念。［3］80在蘇科版初中數學教材中，方程、不等式、函數、統計、概率等內容適合開展數學建模教學活動。從數學建模活動過程看，以現實原型為背景的數學應用類問題（以下簡稱“應用題”），適合開發和組織數學建模活動。基于對蘇科版初中數學教材設置的問題情境的理解和認識，以教材提供的應用題為基礎，筆者建議從以下三個途徑優化應用題教學，培養學生的模型觀念。

1.緊貼生活，呈現實際問題的原生性

原生性是對實際問題屬性的一種描述，是指實際問題應源于學生身邊熟悉的現實生活現象，不加任何簡化、假設和修飾，表現出現實原型的原始樣態。原生性的實際問題與傳統的應用題相比，具有真實性、綜合性、復雜性、開放性、挑戰性等特點，在培養學生的數學化能力上具有重要價值。事實上，在現實生活中，我們遇到的絕大多數問題都是“原生態”的。就數學學科而言，往往需要問題解決者會用數學的眼光對實際問題進行觀察和抽象，從而轉化為數學問題，用數學的語言建立數學模型并求解。因此，在應用題教學中，教師應根據學生的認知水平，以教材上與現實生活緊密聯系的應用題為基礎，結合真實的現實生活對其加以“回溯”，追根溯源，弱化數據信息，還原真實的問題原型，凸顯實際問題的真實性、開放性、原生性，以更“原生”的樣態呈現給學生，創設良好的數學建模情境。

2.合作探究，經歷數學建模的過程性

原生性的問題情境為學生提供了良好的建模載體，這種問題情境具有綜合性、復雜性、開放性、挑戰性的特征，適宜使用“自主+合作”探究的學習方式。教學中，教師應注重引導學生獨立探究與合作探究相結合，積極參與相對完整的數學建模活動，經歷數學建模的過程。數學建模活動一般包括以下幾個環節。

（1）簡化原生性問題，形成現實原型；

（2）現實模型數學化，建立數學模型；

（3）求解數學模型，獲得數學結果；

（4）運用數學結果解釋現實原型；

（5）根據驗證結果，修正模型。

學生只有經歷相對完整的數學建模活動過程，才能從對數學建模的初步感知發展到對數學建模的清晰認識，從而逐步發展模型觀念。

3.分層實施，體悟數學建模的階段性

國內外學者對數學建模內涵的認識是多維度的，比較有代表性的理解有三種：數學建模是一種活動過程，數學建模是一種數學思想，數學建模是一種數學能力。［7］三種理解是學科視點的差異，雖側重點不同，但沒有本質上的差別。基于對高中數學新課標中數學建模的理解，結合新課標中關于“數學建模的基本過程”的分析，筆者將數學建模理解為在數學建模活動過程中培養學生的模型觀念。數學建模是一個相對完整的活動過程，在整個過程中大致可以分為五個階段，每個階段對模型觀念培養的側重點不同。例如，在將原生性問題（現實原型）簡化為現實模型階段，教學側重點在于引導學生分析和思考問題的相關影響因素，剔除次要因素，確定主要因素，對原生性問題進行必要的簡化、假設、抽象，體會數學建模中簡化環節的重要性。又如，在將現實模型數學化建立數學模型階段，教學側重點在于培養學生的數學化能力，具體包括關系梳理、主要因素分析、數據收集、主要問題篩選、提出問題、符號表征等。通過數學建模活動階段性的分步實施，驅動學生體悟建模活動過程，發展模型觀念。

三、教學示例

1.教學內容

蘇科版初中數學八年級上冊第6章第4節“用一次函數解決問題”第1課時。

2.教學目標

（1）能從實際問題中抽象出數學問題，并建立函數模型并求解，在用一次函數表述數量變化及其關系的過程中，發展模型觀念；

（2）經歷“現實問題—數學問題—建立模型—求解驗證”的數學活動過程，積累數學建模活動經驗；

（3）在問題的解決過程中，感悟數學的抽象性、嚴謹性和應用的廣泛性，體會數學的應用價值。

3.教學過程

（1）呈現原生問題

【問題情境1】玉龍雪山

踏進麗江，首先映入眼簾的是那拔地而起的巍巍玉龍雪山。玉龍雪山為云南省麗江市境內雪山群，由13座山峰從南向北縱向排列組成，宛如一條“巨龍”騰越。遠眺玉龍雪山，能看到一條黑白分明的分界線，人們把它稱為“雪線”。雪線以上銀裝素裹、云霧繚繞，雪線以下山林密布、湖水相依。近年來，很多游客包括麗江本地人都說，玉龍雪山上的雪，遠不及以前壯觀了。由于氣候變暖等原因，玉龍雪山的雪線每年都在上升，這樣下去雪線是否會退至山頂而消失？

【教學說明】呈現原生性的問題情境，引導學生用數學的眼光觀eac5969c21f403149b88c6319273de75察現實生活中的問題，從實際問題中抽象出數學問題，建構適切的數學模型并求解，會用求解的數學結果解釋實際問題。在這里，將教材上的原問題情境中的數據剔除（主峰海拔5596m，雪線海拔4500m），意在呈現真實問題的現實原型，凸顯問題情境的現實性、真實性、開放性，激發學生探究問題的興趣。

（2）簡化現實原型

學生活動預設：小組合作嘗試將原生性問題進一步抽象，進行數學化表達，轉化為數學問題，制訂解決問題的方案。

影響因素預設：全球性氣候變暖；冰雪消融量增加，冰雪來源減少；大量游客涌上玉龍雪山與冰川親密接觸，也使得冰川冰雪加快融化。

【教學說明】因原生性問題中沒有提供相關數據，學生一開始是茫然的、手足無措的。但隨著對影響因素的分析，學生逐步認識到要收集主要影響因素的數據，并對問題進行必要的簡化和假設，從現實原型中簡化出現實模型，形成數學問題。

（3）建構現實模型

教師提供數據：主峰海拔5596m，雪線海拔4500m，麗江玉龍雪山冰川與環境觀測站觀測發現2003年至2008年，玉龍雪山雪線上升約50m。

數學問題：玉龍雪山由13座山峰組成，主峰海拔5596m，在海拔4500m處的雪線平均每年上升約10m。假設雪線的高度按此速度不斷變化，幾年后玉龍雪山的雪線將由現在的海拔4500m退至山頂而消失？

【教學說明】在建構現實模型環節，讓學生經歷數據收集、抽象、假設等階段性建模過程，在探究中分析、篩選主要影響因素，確立時間與雪線海拔兩個主要因素，為建立數學模型作鋪墊。結合主要影響因素的數據信息，進一步對現實模型進行數學化表達，形成清晰的數學問題。

（4）建立數學模型

建構模型：玉龍雪山問題情境中的數學模型具有一定的開放性，預設學生會建構不同的數學模型求解。

活動預設：模型1—算術模型：（5596-4500）/10；模型2—方程模型：設經過x年玉龍雪山的雪線將退至山頂，根據題意，得10x+4500 = 5596（求解略）；模型3—函數模型：設雪線海拔為y（m），時間為x（年），則函數表達式為y=10x+4500。

【教學說明】鼓勵學生建立不同的數學模型求解數學問題，體現模型的多樣性，引導學生比較不同數學模型的優劣，凸顯函數模型的優越性。

（5）求解數學模型（略）

【教學說明】教學中教師還可以根據數學模型的求解結果，實施數學學科德育滲透。例如，建設觀測站，修建濕地湖泊群，增加植被覆蓋率，增加地表水體，限制旅游人數等。又如，低碳出行，保護水源，節約用水，保護動物等。

（6）建模活動探究

【問題情境2】停車場收費

某記者自駕前往玉龍雪山調查研究“雪線”最新的變化狀況，準備將小轎車停放在山腳下的小型車停車場，停車場收費公示牌信息顯示：半小時內免費，首小時4元，超過1小時后每半小時2元，不足半小時按半小時計算。（圖片略）

活動要求：根據提供的信息，自主提出有價值的問題，并嘗試解決。（學生先獨立探究，再合作交流，最后推薦組員展示小組的研究成果）

問題預設：小型車停車場是如何計費的？

【教學說明】圖片采集于玉龍雪山附近的停車場，以“原生”的樣態直接呈現，給學生提供一種現實原型情境，有利于驅動學生自主發現和提出有價值的問題，分析問題，建立數學模型（y=kx+b）并求解，經歷完整的數學建模活動過程。

（7）建模作業布置

在確保安全的情況下，拍攝出租車的收費信息，作為數學建模素材，提出有價值的問題，收集相關信息，解決問題，并撰寫研究報告。

【教學說明】通過開放性的建模作業驅動學生綜合運用數學和其他學科的知識與方法，在實際情境中發現和提出問題，抽象出合理的、有意義的數學問題，提出解決問題的思路，設計解決問題的方案，建立適切的數學模型并求解，從而經歷數學建模的基本過程，發展學生的模型觀念。

在初中數學教學中，培養學生的模型觀念既是數學教育最重要的目標之一，也是培養學生核心素養的重要路徑。學生模型觀念的建立不可能一蹴而就，必然是一個綜合性、長期性兼具階段性的過程。這就要求我們初中數學教師既要做好以數學概念、公式、原理等為主的廣義數學模型的教學，也要發掘好以數學應用題、綜合實踐活動等為主的狹義數學模型的教學，著重引導學生感受建立數學模型求解實際問題的過程，經歷相對完整的數學建模活動，逐步培養初中生的模型觀念。

【參考文獻】

［1］孫凱.指向高觀點的數學模型建構教學——以蘇科版“一元一次方程單元復習”為例［J］.內蒙古師范大學學報（教育科學版），2021，34（6）：137-140.

［2］史寧中，曹一鳴.義務教育數學課程標準（2022年版）解讀［M］.北京：北京師范大學出版社，2022.

［3］中華人民共和國教育部.義務教育數學課程標準（2022年版）［S］.北京：北京師范大學出版社，2022：10.

［4］孫凱.近二十年來中學數學建模研究的回顧與展望［J］.中學數學雜志，2021（12）：1-7.

［5］孫凱.從問題類屬談初中生數學建模能力培養［J］.數學通報，2020，59（12）：30-33.

［6］孫曉天，沈杰.義務教育數學課程標準（2022年版）課例式解讀［M］.北京：教育科學出版社，2022：95-96.

［7］劉偉.初中生數學建模能力培養研究［D］.曲阜：曲阜師范大學，2020：5.