任務設計結構化，助推核心素養(yǎng)進階

在小學數(shù)學教學中，數(shù)學表達能力、思維能力、問題解決能力是學生核心素養(yǎng)重要的構成部分。在教學過程中，充分發(fā)揮學生主體作用，調動學生學習的積極性，能切實強化學生的學習興趣。同時，完成結構式任務，能幫助學生將所學知識應用到實際中，從而培養(yǎng)學生的獨立思考能力和自主學習能力，進而使其核心素養(yǎng)得到提高，并在合作中相互溝通、相互配合，從而發(fā)展團隊合作精神和人際交往能力。

“三位數(shù)乘兩位數(shù)”是學生在學習運算知識過程中要掌握的重要內容，教師采用結構化的任務設計能使學生對算理和算法有更深入的理解，從而使其逐漸提高運算能力，較好地解決實際問題。為此，教師要注重發(fā)揮“任務”的優(yōu)勢，助推學生核心素養(yǎng)的進階發(fā)展。

一、整合結構化材料，強化問題解決能力

在現(xiàn)代教育背景下，整合結構化學習材料是培養(yǎng)學生核心素養(yǎng)的重要途徑。結構化學習材料倡導整體感悟、整體融合，使學生在掌握知識的同時，理解知識的邏輯關系，能舉一反三地真正融通、建構知識，深度理解學習內容，充分感受和把握數(shù)學的知識結構和方法結構，并形成比較完善的數(shù)學認知結構和思維結構。

《義務教育數(shù)學課程標準（2022年版）》指出數(shù)的運算重點在于經(jīng)歷算理和算法的探索過程，理解算理、掌握算法，體會數(shù)的運算本質上的一致性，形成運算能力和推理意識。同時指出，教師要整體把握教學內容，注重教學內容的結構化。具體是指能夠運用種子概念將不同類數(shù)的同一運算和相同類數(shù)的不同運算建立結構化的聯(lián)系，讓學生理解數(shù)的運算本質。

下面以“三位數(shù)乘兩位數(shù)”教學為例，闡述結構化學習材料。

整體呈現(xiàn)結構化組題：

①125×4 ②25×24 ③125×12 ④125×24 ⑤105×20 ⑥150×20 ⑦745×37

師：你能一眼看出哪些算式的積？

生1：105×20，先算105×2，三位數(shù)乘一位數(shù)可以口算，再在結果后面加一個0。

追問1：為什么最后要加0？

生2：150×20，先算15×2，再在結果后面加兩個0。

追問2：最后要加兩個0，理由是什么？

生3：25×24也可以口算，25×24=25×4×6=600。

生4：125×4=125×8÷2=500或125×4=100×4+25×4=500。

生5：因為125×4=500，所以125×12=125×4×3=1500。

生6：125×4，125×12，125×24都是有聯(lián)系的，125×24=125×4×6=125×8×3=125×12×2=3000。

追問3：125×4，125×12，125×24有怎樣的聯(lián)系？

經(jīng)過討論發(fā)現(xiàn)，125×4，125×12，125×24三個算式的第一個因數(shù)相同，第二個因數(shù)有倍數(shù)關系，所以積也有倍數(shù)關系，為積的變化規(guī)律的系統(tǒng)學習打下扎實的基礎。

以組題的形式呈現(xiàn)整體結構化學習材料，引導學生回顧、類比、遷移整數(shù)乘法。①將口算、巧算以及積的變化規(guī)律融為一體，整體呈現(xiàn)，整體建構。②將多位數(shù)乘一位數(shù)、兩位數(shù)乘兩位數(shù)的方法遷移到三位數(shù)乘兩位數(shù)，利用舊知學習新知，利用舊知建模新知。③關注計算的整體性和一致性，理解算理方法的多樣化。

在教學實踐中，教師通過設計結構化學習材料，不僅能幫助學生更好地理解和掌握所學知識，還能提高學生解決實際問題的能力。

二、創(chuàng)建任務式學習活動，提升主動探究能力

任務式學習主張在任務驅動下支持學生自主探索、協(xié)作學習，實現(xiàn)預期的教學目標。在小學數(shù)學教學中，教師創(chuàng)建任務式學習活動，能有效地指導學生進行自主學習，提高其解決問題的能力，發(fā)展學生的核心素養(yǎng)。任務式學習提倡學生對特定問題進行研究，嘗試提出假設、探索和證明，并從中獲取知識和技能。同時，在教學過程中，學生可以將所學知識應用到實際情境中，并逐漸養(yǎng)成獨立學習、探究的習慣。另外，任務式學習還可以使學生在課堂上進行協(xié)作與溝通，培養(yǎng)學生的團隊協(xié)作意識和交際能力。

在教學“三位數(shù)乘兩位數(shù)”時，教師設計一系列任務式教學活動，使學生能循序漸進地去探索和解決問題。下面闡述如何創(chuàng)建估算教學的任務。

師：745×37的積大約是多少？和正確的積比，是大了？還是小了？

生1：2000多。

生2：20000多。

生3：30000不到。

生4辯解：2000多肯定錯了，這道題的積應該是五位數(shù)。

生5：如果把745×37看成700×30也有21000，積怎么可能是2000多呢？

生6：如果把745×37看成750×40，把兩個因數(shù)都估大了積是30000，所以精確的積肯定小于30000。

師：看來745×37的積在20000～30000之間。

追問：那么三位數(shù)乘兩位數(shù)的積可能是幾位數(shù)？

通過爭議、討論，得到□□□×□的積是三位數(shù)或四位數(shù)，□□×□□的積是三位數(shù)或四位數(shù)，□□□×□□的積是四位數(shù)或五位數(shù)。

借助圖解：

100×1=100 999×9＜10000

10×10=100 99×99＜10000

100×10=1000 999×99＜100000

任務式學習主張從低通路遷移轉向高通路遷移，從散到聚，從碎到合。①培養(yǎng)學生的估算習慣，整體建構估算意識。②利用數(shù)軸，整體推進多位數(shù)乘法積的位數(shù)的推理，提升高階思維能力。

杜威提到過三種水平的教學，第一種水平的教學是把一節(jié)課就當一節(jié)課教，第二種水平的教學會關注學科內知識的融會貫通，第三種水平的教學則是聯(lián)系真實來思考教學。任務式學習設計的本質就是要聯(lián)系實際，通過遷移，引導學生找到各知識點之間的聯(lián)系，構建合理的知識網(wǎng)絡，提升學生主動探究的能力。

三、核心問題式引領，提升數(shù)學運算能力

在數(shù)學教學中，教師以問題為中心，引導學生進行思考、探究，能提高其數(shù)學運算能力。在小學數(shù)學教學過程中，教師對核心問題進行設計，讓學生體驗估算、筆算、歸納和總結的過程，從而確保學生掌握特定的運算方法，培養(yǎng)抽象思維和邏輯推理能力。在以問題為導向的基礎上，關注學生在解題過程中的思維發(fā)展，讓其在對所學知識進行理解與掌握的基礎上，提高其數(shù)學素養(yǎng)和解決實際問題的能力。

計算教學的核心是算理與算法，算理是依據(jù)，算法是基礎，計算教學從算理開始，算理清晰才可以生長算法，在理解算理的基礎上生長多種算法，它們相互依賴，相互依存，相互共生，并能在具體的情境里靈活解釋算式各部分的意義。

在教學“三位數(shù)乘兩位數(shù)”時，教師設計核心問題，還能使學生在思考與探究的過程中積累應用已有知識解決新問題的經(jīng)驗，并使其養(yǎng)成獨立思考、自主學習的習慣。

還是以“三位數(shù)乘兩位數(shù)”為例，呈現(xiàn)例題。

例：一列火車以每小時125千米的速度從杭州開往北京，12小時到達，火車行駛了多少千米？

核心問題1：用豎式計算125×12，豎式中的每一步表示什么意思？

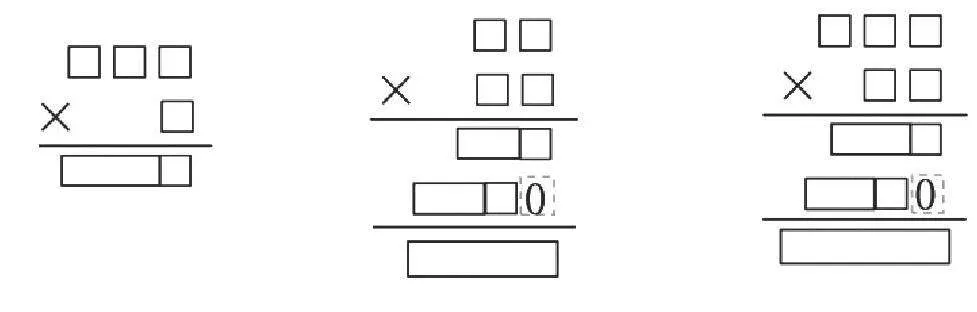
學生表達如下：

在豎式教學的過程中，面積模型、橫式、豎式同時呈現(xiàn)，進行對比分析，不僅引導學生深刻理解筆算算理，還有對筆算、口算、估算三者關系的深度建構。面積模型中筆算的每一步都是求小長方形的面積，借助直觀，從“小碎步”到“跨大步”，讓學生經(jīng)歷從算理碎片化到結構化的過程，去除學生碎片化的“點對點”的表達，而是用個位的2去乘125得到250個一，再用十位的1去乘法125得到125個十，達到異中求同、整體建模的過程。

核心問題2：對比三位數(shù)乘一位數(shù)，兩位數(shù)乘兩位數(shù)，三位數(shù)乘兩位數(shù)，它們有什么相同與不同的地方？

生：三位數(shù)乘一位數(shù)的積是一層，兩位數(shù)乘兩位數(shù)、三位數(shù)乘兩位數(shù)的積是兩層。

追問1：積的層數(shù)跟哪個因數(shù)有關？有沒有積是三層的乘法算式？

生2：有的，如125×125，積就有三層，積的層數(shù)跟第二個因數(shù)有關系。

追問2：每層積表示的意義有什么不同？

生3：第一層積都表示幾個一，第二層積表示幾個十，第三層積表示幾個百……

生4補充：將125×12寫成12×125，積也有三層。

在此過程中，以核心問題為引領，以層為基，統(tǒng)領理法，找尋共性，深化理解，融會貫通。在對問題進行探究和解決的過程中，學生對現(xiàn)有知識進行學習，獲得新計算方法，培養(yǎng)觀察、比較、概括等思維能力，養(yǎng)成耐心計算和仔細驗算的學習習慣。核心問題式的引領讓學生在持續(xù)思考與探究中掌握特定的計算方法，提高數(shù)學操作能力和核心素質，為后續(xù)的數(shù)學學習打下扎實的基礎。

四、構建可及式評價，促進核心素養(yǎng)進階

可及式評價是一種以學生為中心的評價方法，教師利用多樣化、分級式的評價方法，讓每一位學生都可以了解自身的優(yōu)缺點，從而推動學生核心素養(yǎng)的發(fā)展。此種評價方法側重于最后的結果，并且重視學生在學習中的表現(xiàn)與能力的發(fā)展。在教學中，教師建立一套科學、合理的可及式評價體系，能對學生的學習情況進行實時掌握，并對其進行有針對性的反饋與引導，使其能更好地理解自己的學習目標，提高學習效率。同時，可及式評價也重視學生的個別差異，關注學生的學情，激勵學生主動學習，從而使其養(yǎng)成良好的學習習慣，樹立學習數(shù)學自信。在教學“三位數(shù)乘兩位數(shù)”時，教師建立分階段的可及式評價方法，能使學生的核心素養(yǎng)得以提高。

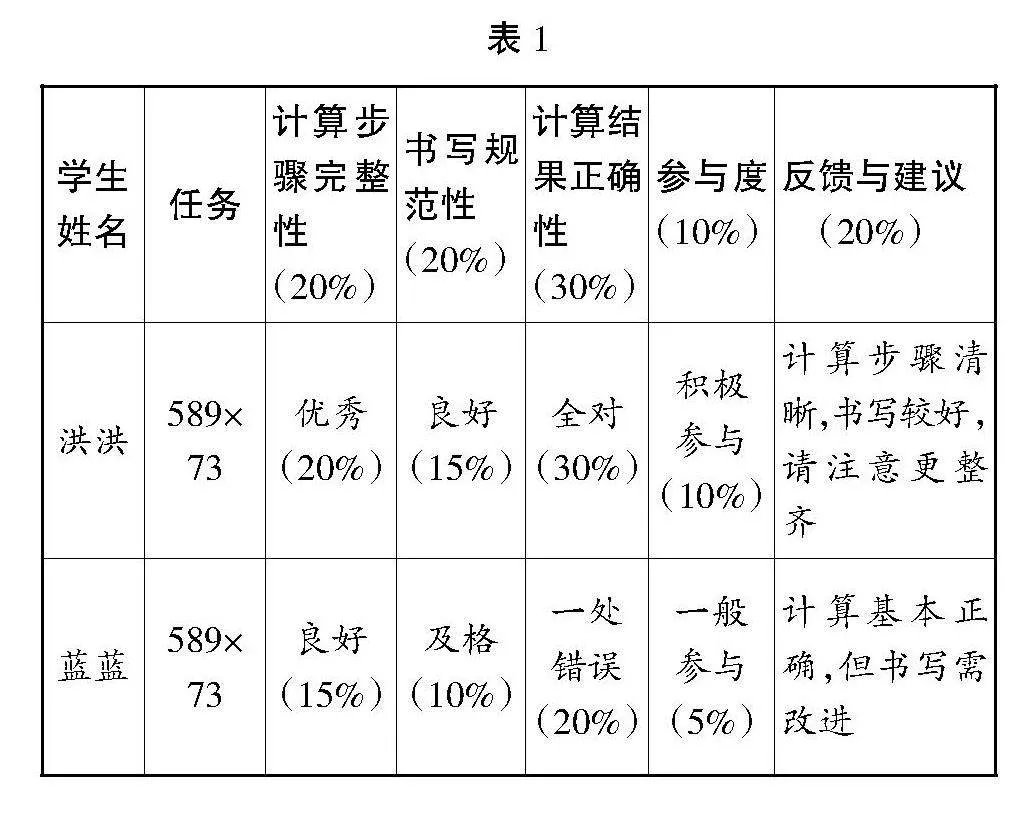
在初步理解階段，教師設計簡單的學習任務，要求學生嘗試解決“589×73”（連續(xù)進位）這一問題，學生解題后，教師針對學生的計算過程進行評價，關注學生的計算步驟和書寫標準，并進行及時的反饋及評價（見表1）。其中，對表現(xiàn)較好的學生，教師則要給OsDglSHMJDktY8KWhn9XjSvGjZ9FRWKOAs496hx0/xY=予鼓勵，驅動再接再厲。對于出現(xiàn)錯誤的學生，教師則可進行個性化輔導，使其改正錯誤，并掌握正確的三位數(shù)乘兩位數(shù)運算方法。

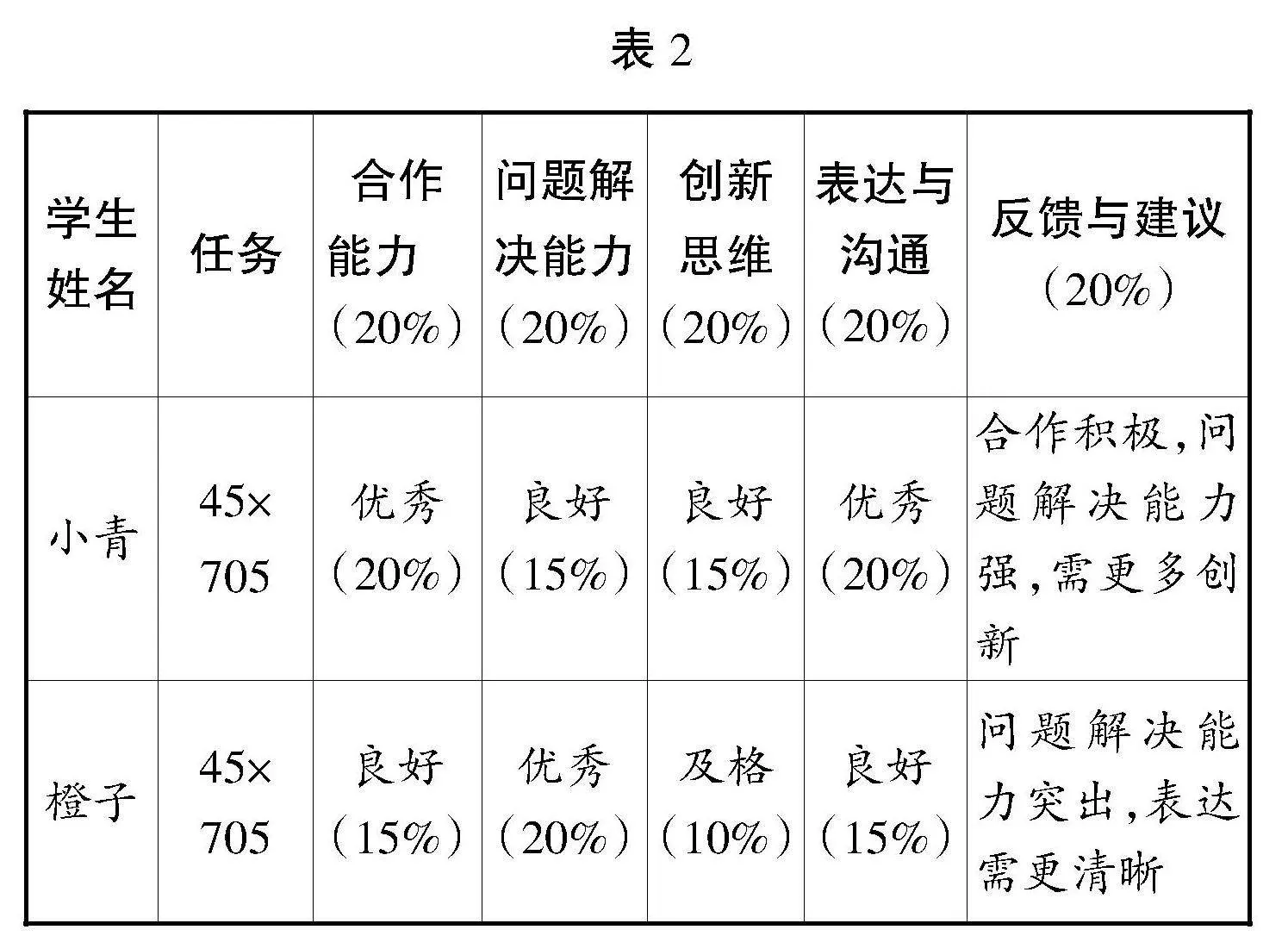
在深入探究階段，教師設計更具挑戰(zhàn)性的學習任務，要求學生在小組內討論及合作解決“45×705”（因數(shù)中間有0）這一問題。在合作學習中，學生可以相互交換計算方法、思想，在相互借鑒、相互學習的基礎上獲得進步。在分組演示與反饋階段，教師鼓勵學生就自己的計算步驟、思想進行交流，并給出具體的可及性評價意見（見表2）。

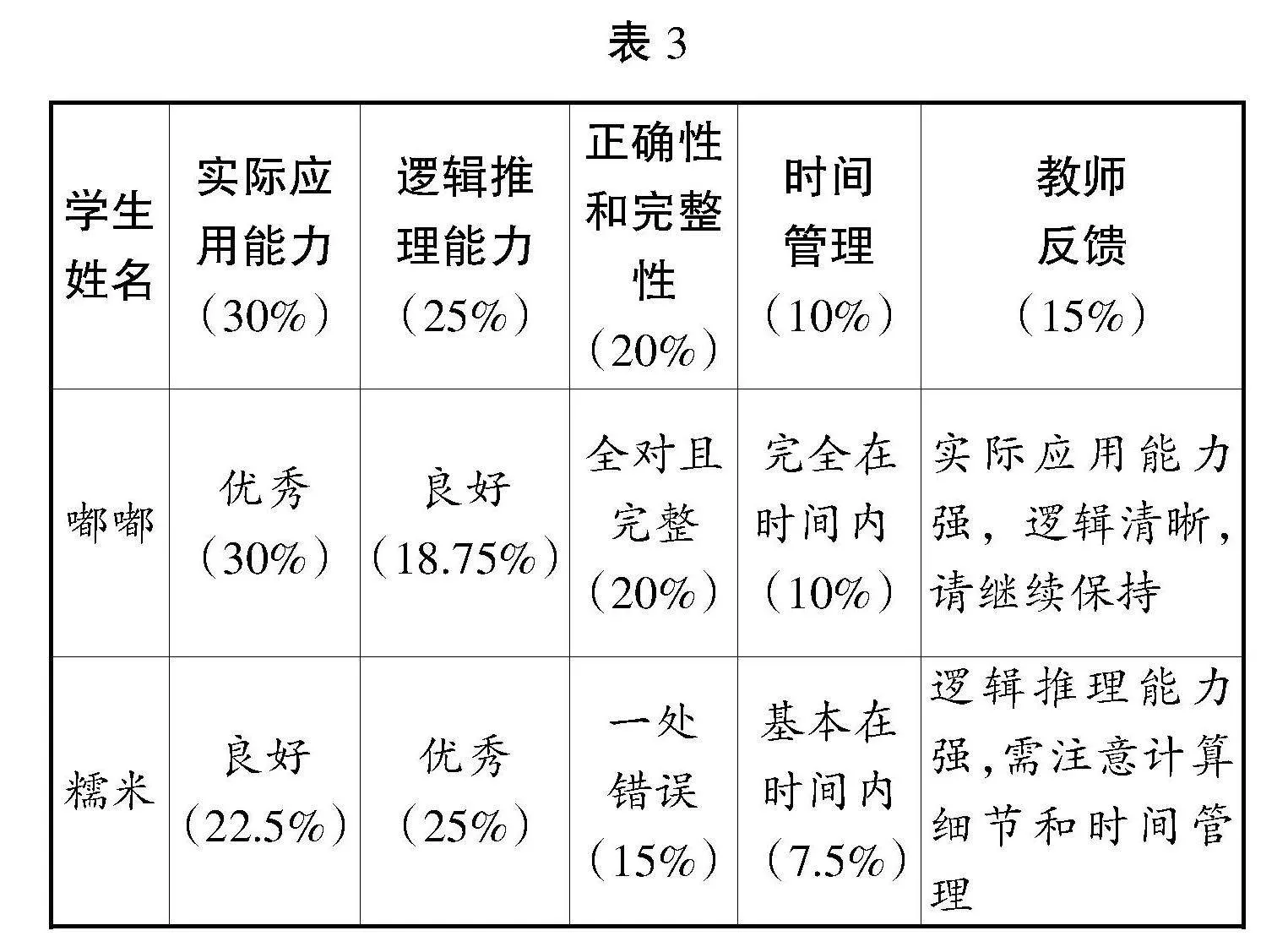
在提升應用階段，教師則需設計實用性問題。教師在這一階段進行終結性評價，關注學生是否能夠將所學知識應用到實際問題中，并給予綜合評價（見表3）。

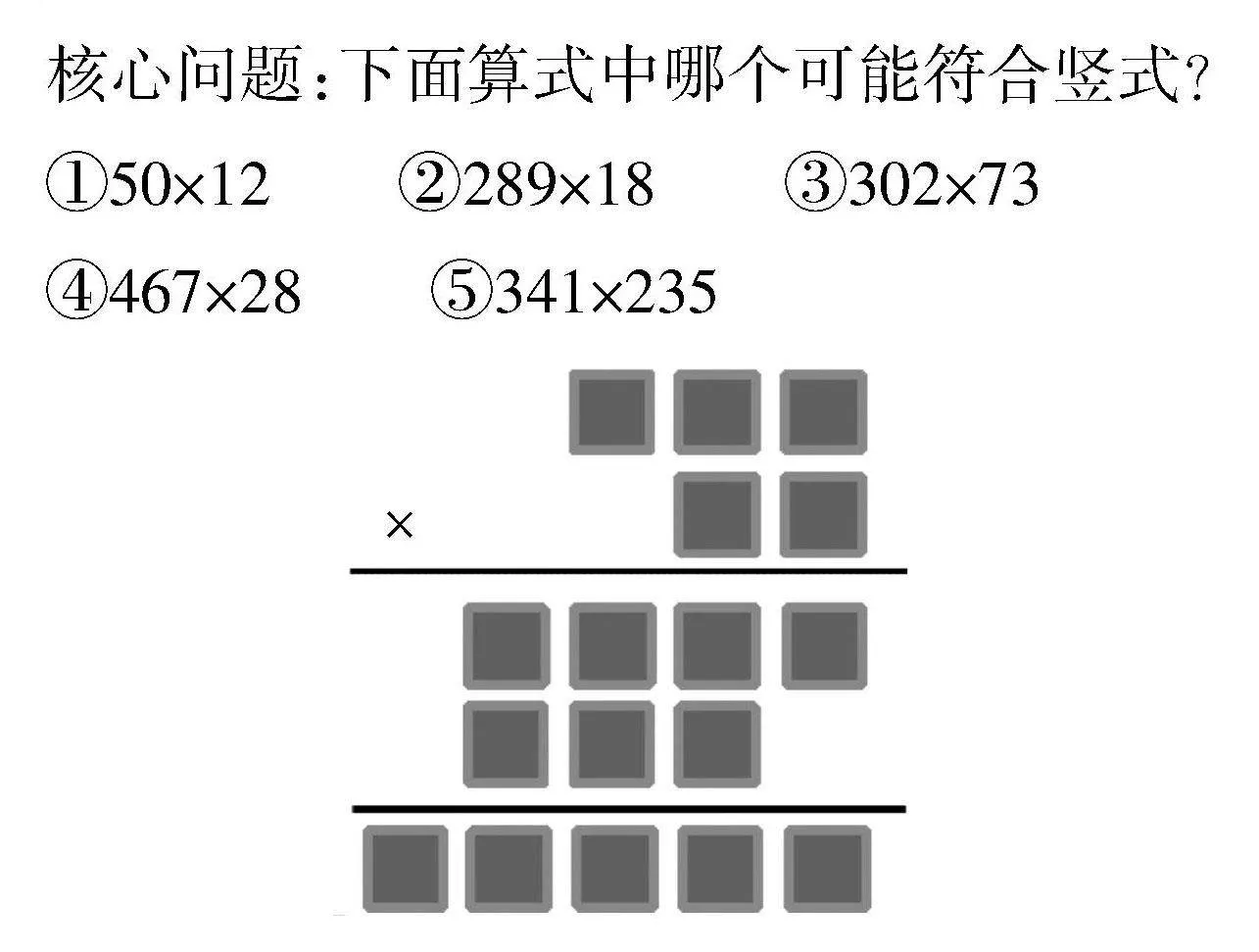
核心問題：下面算式中哪個可能符合豎式？

①50×12 ②289×18 ③302×73

④467×28 ⑤341×235

經(jīng)過討論發(fā)現(xiàn)：①是兩位數(shù)乘兩位數(shù)，不符合。②的積是四位數(shù)。③的積第一層的位數(shù)不對，第二層的位數(shù)也不對。④有可能。⑤是三位數(shù)乘三位數(shù)。

教師引導學生練習的過程中，使學生形成多元的方法策略，深化數(shù)學思想方法，培養(yǎng)學生運用所學知識解決實際問題的能力。核心練習體現(xiàn)了層次性和結構性，學生通過練習對所學數(shù)學知識重復接觸和反思，成為學習過程中重要的實踐活動。這樣的設計呈結構性，不是單純地以某一個題呈現(xiàn)，而是綜合性的體現(xiàn)，以一組題為線索，對口算、估算、筆算進行有效的聯(lián)系，發(fā)展學生能力，啟迪思維，發(fā)展智力。這樣的溝通與連接，無異于給了學生另一雙眼睛，讓學生知道知識并非孤立的。

教師在評價學生時，主要評價學生能否正確、清晰地表達自己的解題思路。對學習表現(xiàn)優(yōu)異的學生，教師要給予適當?shù)谋頁P與獎勵，以鼓勵其堅持下去。針對學習困難的學生，教師要采取個體化的方式，幫助其解決問題。在一系列訓練和評價中，學生在學習中提高解決問題的能力、協(xié)作能力和運用能力。可見，可及性評價的實施，能讓每一位學生都清楚地了解自身的優(yōu)點與不足，并能清楚地知道自己要努力的方向，逐漸提升核心素養(yǎng)，為后續(xù)學習打下良好的基礎。

因此，“三位數(shù)乘兩位數(shù)”教學中，任務設計結構化能使學生掌握基本的運算方法，培養(yǎng)邏輯思維和解題能力。同時，教師將結構式材料、任務式學習、核心問題式引領等有機地融合在一起，讓學生在各個學習階段都能有清晰的目標與方法，并不斷提升數(shù)學素養(yǎng)。在后續(xù)的數(shù)學教學中，教師仍要把學生的個性與能力的發(fā)展放在第一位，運用各種教學方法與評價方法，充分調動學生的學習積極性，提高其自主學習能力，助推核心素養(yǎng)的進階。

（作者單位：杭州師范大學附屬未來科技城學校）

編輯：曾彥慧

作者簡介：楊青（1976—），女，漢族，浙江杭州人，高級教師，主要研究方向：小學數(shù)學教學。