運用“嘗試問題組”架構高中數學探究課堂

【摘 要】“嘗試”就是為了解決探究主題問題而進行猜想、試驗、反思、再猜想的一種試探性活動。在高中數學教學中，教師可以從學生的認知體驗出發構建“嘗試問題組”，即結合學生的思維特點，創設讓學生具身體驗的問題鏈，讓學生通過猜想教學關聯、構建數學模型、驗證數學猜想，開展自主探究、合作探究，引導學生深入思考。

【關鍵詞】高中數學；嘗試問題組；數學探究活動；圓的切線與切點弦

【中圖分類號】G633.6? 【文獻標志碼】A? 【文章編號】1005-6009（2024）19-0049-04

【作者簡介】楊靜，江蘇省東海高級中學（江蘇東海，222399）教師，一級教師，獲江蘇省“教海探航”征文競賽“杰出水手獎”。

《普通高中數學課程標準（2017年版2020年修訂）》（以下簡稱“新課標”）提出，“數學探究活動是圍繞某個具體的數學問題，開展自主探究、合作探究并最終解決問題的過程……是運用數學知識解決數學問題的一類綜合實踐活動。”教學中，教師可以圍繞探究主題，進行有效的問題設置，將探究主題化整為零，以遞進式問題鏈的形式，引導學生層層深入地進行思考探究，讓學生參與到數學知識的發生發展過程中，體驗類比、歸納、演繹等數學研究方法，深化對數學知識的理解。

一、嘗試問題組：探究性活動的內驅力

高中數學課堂應以學生認知體驗為起點，豐富學生的思維體驗，保障學生思維能力的發展，這樣才能深化學生學習的內驅力。

（一）嘗試問題組：基于認知體驗的問題設置

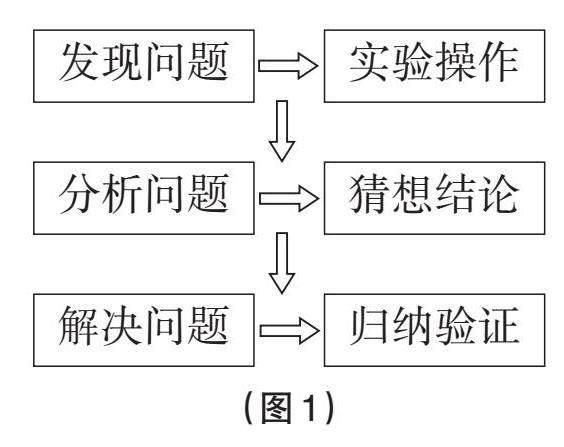
“嘗”即分辨滋味，旨在檢驗探究主題的深度；“試”即試驗猜想，旨在將獨立思考或交流合作產生的命題付諸實踐。“嘗試”就是為了解決探究主題問題而進行的一系列猜想、試驗、反思、再猜想。高中數學探究活動中“嘗試問題組”的設置，即從“嘗試”的角度出發，結合學生的思維特點，創設讓學生具身體驗的問題鏈，讓學生通過實驗操作、猜想數學關聯、構建數學模型、驗證數學猜想，在數學探究活動中通過“嘗試”進行思考、反芻，從而培養學生思維的廣度和深度。（見圖1）

[發現問題] [實驗操作] [猜想結論] [分析問題] [解決問題] [歸納驗證] [（圖1）]

（二）嘗試問題組：數學探究活動的應然選擇

數學探究活動是基于培養學生的創新意識開展的綜合實踐活動。數學探究活動作為一種小型的研究性思維活動，既能培養學生發現和提出有意義的數學問題的能力，又能使學生在探索和表述的論證過程中提高表達和交流的能力，積累數學活動經驗，發展數學抽象、邏輯推理、直觀想象等數學學科核心素養，養成獨立思考和合作交流等良好習慣。《問題與探究》為蘇教版高中數學教材的每章章末欄目之一，是相應章節內容的一個延伸，內容主要圍繞一個探究主題，分為“問題”和“探究”兩個方面，讓學生結合所學知識，探究解決問題的方案與路徑，為拓展學生思維、培養學生的創新意識和應用意識提供了載體，是開展數學探究活動的良好素材。

“嘗試問題組”旨在引導學生發現和提出有意義的數學命題，讓學生通過對問題組的獨立思考和合作交流，激發自我完善、自我提高的動機，培養問題解決過程中的相互啟發、相互促進的合作意識；讓學生經歷完整的探究過程，增強不同層次、不同水平的學生在探究活動中的認知獲得感，從而培養學生的探索精神、創新精神和實踐能力，讓學生更深入地思考、整合知識與經驗，將批判性思維內化成自身的經驗體系。

二、課堂實踐：探究性活動的收斂架構

“圓的切線與切點弦”是蘇教版普通高中數學教科書選擇性必修第一冊第二章《圓與方程》的章末探究課，是《圓與方程》章節知識的延伸與拓展，也是后續圓錐曲線相關的內容學習的起點和基礎。本節課旨在通過研究幾何圖形的性質和位置關系，讓學生體會數形結合、轉化化歸等多種數學思想，培養學生的直觀想象、數學抽象、邏輯推理等數學學科核心素養。下面筆者以“圓的切線與切點弦”教學為例，具體闡釋在高中數學課堂教學中，如何以“嘗試問題組”引領學生開展數學探究活動。

（一）目標引領：研究主題從“學情適合”出發

教學目標是數學探究課堂的出發點和歸屬點，教師首先要從學情出發，設置適合學生學情的課堂目標。整體探究目標要明確，學生圍繞整體目標進行嘗試，教師圍繞學生解決問題中產生的動態問題將課堂目標完善、落實。

整體目標設置要從學情出發，要符合大部分學生的認知水平，讓每一位學生都能參與到探究活動中，目標內容要具體明確、導向性強。同時保障主體目標的連貫性、延展性、可持續性，讓學生在嘗試問題組的引領下，養成良好的思考習慣，提升學習能力。

在學完《圓與方程》章節之后，學生已經能從代數角度研究點、直線、圓之間的關系，初步具備研究解析幾何的直接經驗，具有一定的圖形識別、問題發現及探究推理能力。圓的切線與切點弦中，點、線、圓的關系復雜，想要厘清并掌握其關系對數形結合的思想要求較高，需要學生具有良好的直觀想象、邏輯推理能力。

基于上述學情分析，在“圓的切線與切點弦”的教學中，筆者制定了以下整體目標：（1）掌握求解“過圓上一點的切線方程”的方法；（2）通過操作實驗，提出合理猜想，體會問題探究的方法；（3）體驗探究方法與研究方法的類比，滲透變換主元與方程（組）思想，培養觀察、歸納、反思的能力。

除此之外，學生還可以根據自身的學習特點和認知水平，有選擇地加深或拓寬某一目標，讓目標更具適用性。教師還應針對每個學生的研究效率及目標完成度給出總體評價，對于高效的學生給予參照式評價從而發揮榜樣作用，對于低效的學生給予指向性評價進行引導，以促進學生更進一步地思考，培養學生的探索精神，引導學生自主發展。

（二）問題引領：探究活動從“操作嘗試”啟程

數學探究活動是主體與客體交互生長的復雜過程，需要教師和學生在思維、意志、動機上的相互參與、相互配合，教學時，教師要以學生為主體，從學生的學習需求出發構建探究問題，這個過程還需要教師的整體調控。結合探究主題，師生首先師生確定研究方式：提出問題—操作實驗—交流討論—驗證猜想。

1.嘗試問題直觀的遞進設置

在問題設置上，教師首先要結合學生的認知特點，讓學生在探究抽象的數學問題時感受數學的直觀性，激發學生的學習興趣與探索欲，為學生進一步的研究指明方向。因此，在教學“圓的切線與切線弦”時，筆者首先設置了如下引例。

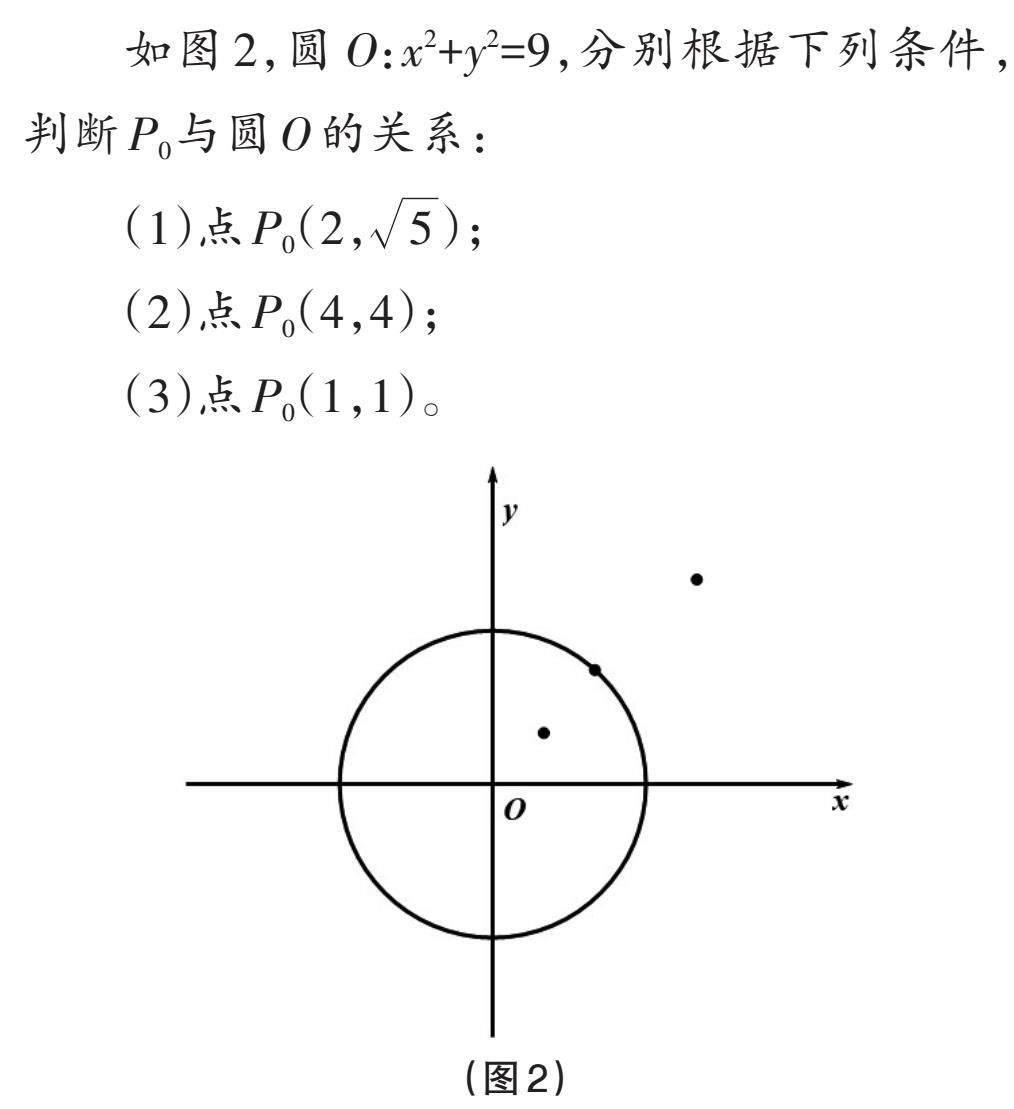
如圖2，圓O：x2+y2=9，分別根據下列條件，判斷P0與圓O的關系：

（1）點P0（2，[5]）；

（2）點P0（4，4）；

（3）點P0（1，1）。

【設計意圖】上述教學從引例出發，讓學生明確本節課是研究點、線、圓位置關系的問題探究課。通過特殊點的設置，引導學生學會通過代數方法判斷點與圓的位置關系，并了解與點有關的切線問題的著力點，從而確定本節課的研究路徑：點在圓上—點在圓外—點在圓內。

2.嘗試問題統一的結構設置

高中數學教學應由淺入深，從學生的認知體驗出發，逐步引導學生歸納探究問題的研究路徑與研究方案。因此，嘗試問題采用統一的結構設置，從路徑嘗試、方案嘗試、操作嘗試、猜想嘗試、驗證嘗試五個方向引導學生探討解決問題的路徑與方案，從而提出合理猜想并加以證明。

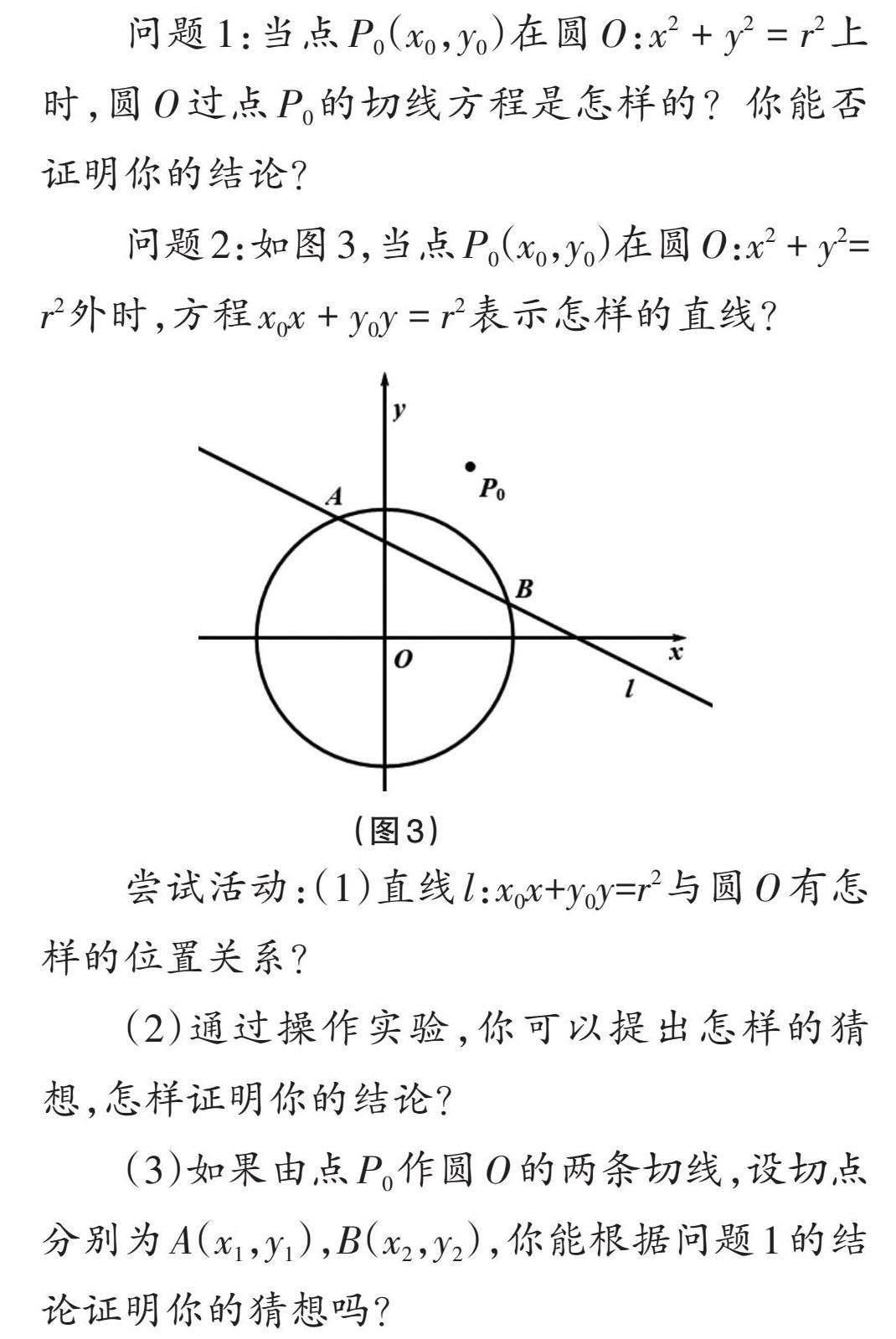
問題1：當點P0（x0，y0）在圓O：x2 + y2 = r2上時，圓O過點P0的切線方程是怎樣的？你能否證明你的結論？

問題2：如圖3，當點P0（x0，y0）在圓O：x2 + y2= r2外時，方程x0x + y0y = r2表示怎樣的直線？

嘗試活動：（1）直線l：x0x+y0y=r2與圓O有怎樣的位置關系？

（2）通過操作實驗，你可以提出怎樣的猜想，怎樣證明你的結論？

（3）如果由點P0作圓O的兩條切線，設切點分別為A（x1，y1），B（x2，y2），你能根據問題1的結論證明你的猜想嗎？

本環節的教學中，由問題1結論探尋對于點在圓外和點在圓內時，直線l的幾何意義。教師基于學生認知體驗的“最近發展區”，引導學生開展自主探究，通過嘗試活動引導學生猜想直線為切點弦AB所在直線，并給出代數證明。換個角度，從點P0作切線，應用問題1的結論進行證明，實現知識的遷移與應用。

問題3：如圖4，當點P（x0，y0）在圓O：x2+y2=r2內（異于O）時，你能發現直線x0x+y0y=r2與圓有怎樣的位置關系？

嘗試活動：（1）直線l：x0x+y0y=r2與圓O有怎樣的位置關系？

（2）你能作出與點有聯系的切線嗎？

（3）根據你的操作，可以得到怎樣的猜想？

通過操作實驗的設置，學生嘗試探究的方法，激發學生的探究興趣，從而體會發現問題、提出猜想的認知過程。問題3是一個開放性的研究問題，學生需要根據自己的猜想進行多次操作試驗，讓思維經歷對峙、分化、共鳴的過程，最后得到合理猜想。主要有兩個角度：（1）從點P0出發任意作一條弦，過弦的兩端作圓的切線，切線的交點在直線上；（2）在直線l上任取一點，過點作圓的切線，切線的交點為點P0。

3.嘗試問題開放的思維延展

在數學探究活動中，基于學生的個體差異，教師應留給學生充分交流探討的空間，讓學生圍繞一節課的探究主題，以其所掌握情況為支點，通過不斷的思考、嘗試、反思，形成自己的思維鏈。教師在探究過程中只有關注學生的思維過程，確定學生的認知水平，才能充分地掌握學生的學習動態，引導學生總結反思，從而實現探究方法和證明方法的正遷移。

高中數學課堂教學要從學生的認知水平出發，讓學生用已有經驗嘗試解決“新生”問題，這樣才能激發學生的求知欲，進而培養學生的學習能力、創新能力。問題探究課堂可以從精心設計適合學情的“嘗試問題組”出發，構建適合學生思維發展的課堂空間，營造以學生為主體的思維學習場，增強學生數學抽象能力生成的內驅力，讓學生開放的思維收斂在正向的維度，讓高中數學教學更具實效性。

【參考文獻】

［1］中華人民共和國教育部.普通高中數學課程標準（2017年版2020年修訂）［S］.北京：人民教育出版社，2020：18.

［2］任小平.基于數學核心素養的“教”與“學”探究［J］.數學教學通訊，2021（33）：35-37.

［3］陳佰林.“減負增效”下數學學科教學之路［J］.上海教育，2022（Z1）：77-78.

［4］李尚志.核心素養滲透數學課程教學［J］.數學通報，2018，57（1）：1-6，14.