習題變式 撬動思維

曹志飛

［摘 ?要］ 在小學階段，習題變式是教學的重點與難點，它需要學生具備良好的數學思維和創造力，靈活解決變式問題是學生學習能力的體現。文章以幾道小學習題為例，對變式教學進行初步研究，旨在創新變式教學策略，促進學生深度學習，培養和發展其高階思維，最終提升數學素養。

［關鍵詞］ 習題變式；數學思維；深度學習；高階思維

“習題變式”是指對于某種習題，通過不斷更改問題的情境或者思維的角度，在保證習題本質特征不變的情況下，習題的非本質特征不斷變化。習題變式對學生的思維能力以及應變能力等方面提出了較高的要求。因此，采取何種措施來更好地實施“變式教學”顯得意義重大。本文提出幾種常見的教學策略，有意識、有目的地引導學生從“變”中發現“不變”的本質，從“不變”中窺探“變”的模式及規律，打通知識脈絡，發展學生思維，穩步提升學生的數學能力。

一、直接變式，熟知解題方法

在變式教學中，“夯實基礎”和“循序漸進”是第一要義。因此，引入簡單、基礎的直接變式是最關鍵的第一步，直接變式是對于同一類型題目解題方法與技巧的習得。直接變式可以分為形式變式與可逆變式兩種［１］，形式變式可以分為情境變式、數據變式以及兩種方法結合的變式。當然，不論何種形式的直接變式，其目的都是讓學生加深對各種典型習題的理解，熟知解題思路與方法。

比如，教師可以進行針對性的習題變式訓練：學校的體育館要添置一批新的籃球和足球，其中籃球有20個，足球有30個，已知籃球和足球的單價分別為80元和60元，一共需要花多少錢？

第一種是“情境變式”。教師可以將“體育館”改成“圖書館”，“籃球”以及“足球”則可以變成任意兩種書的書名。在實際解題中，學生發現這種形式的變式不會對題目的解法及結果產生本質上的影響，反而能在不斷的變式訓練中從本質上理解“單價×數量=總價”這一公式。

第二種是“數據變式”。“運算錯誤”常常是大多數學生的通病，因此，在學生能大致掌握解題套路而又出現運算錯誤的情況時，教師可對原題的數據進行改動，幫助學生進一步鞏固與提升計算水平。

第三種是“綜合變式”。在這種變式中，如果教師只是進行“1+1=2”式的變式，即純粹地對上述兩種方法進行堆疊，則意義不大。為了能起到“1+1＞2”的效果，教師可將題目改為：小汽車與客車分別從A地與B地同時相向而行，小汽車每小時行駛80千米，客車每小時行駛70千米，5小時后相遇，兩地相距多少千米？可以看出，在改變情境后，學生需要用到“速度×時間=路程”這一公式。雖說改變了公式，但從本質上講，總價公式與路程公式屬于同一認知層面、同一結構以及同一難度的兩個公式。如此一來，學生便能對這種同一類型的題目有更為全面的認知，同時也能起到鍛煉計算能力的作用，取得“1+1＞2”的教學效果。

第四種是“可逆變式”。教師可以將原題變為：學校的體育館花費3400元購買了20個籃球和30個足球，已知籃球的單價為80元，足球的單價是多少？在這種變式下，原來的總價變成了條件，原來的單價則變成了結論。在實際教學中可以發現，只要學生明白了此題考查的是單價、數量與總價之間的關系，通過逆向思考，便能順利地解決問題。總之，所有形式的直接變式都是較為基礎和簡單的，是學生必須要掌握的。當然，對于教師而言，引導學生把握題目的結構與本質，這是最核心的東西。這樣一來，無論題目的情境、數據、條件以及結論如何變化，學生都能熟知解題方法，掌握數學思想。

二、間接變式，提升思維能力

如果說直接變式是一種橫向的、同一水平層面的變式，那么間接變式則是一種縱向的、垂直層面的變式［２］。通俗地講，間接變式可以將一個問題變得復雜且富有層次性，解題時學生需要對題中的各種條件抽絲剝繭，最終撥開問題的迷霧來解決問題。同樣地，間接變式可以分為拓展變式和對比變式。當然，無論是何種形式的間接變式，其宗旨都是為了提升學生的邏輯思維能力和判斷能力，從而逐步增強學生數學能力。

比如，教師對習題進行間接變式處理：超市新進了一批牛奶和餅干，共500千克，已知牛奶的數量為40箱，每箱重量為10千克；餅干的數量為25箱，則每箱餅干的重量為多少？

第一種是“條件的拓展”，教師可以對原題中的一些直接條件進行間接化的處理，將題中的“餅干的數量為25箱”這一條件改為“餅干的數量要比牛奶的數量一半多5箱”。可以看出，這種變式方法對于原題中“餅干的數量”這一直接給出的量設置了障礙，學生需要根據牛奶的數量來求出餅干數量。在這種變式下，學生只要能在熟知解題方法的基礎上，學會多思考一步，審清題意，搞清邏輯，題目便可迎刃而解。

第二種是“問題的變化”，教師可以改變原題的情境與問法，比如將題目改為“超市原本計劃上半年賣出660箱牛奶，但實際上每個月多賣出22箱，則實際上多少個月完成了銷售目標”。在此題中，“數量×月份=總數量”這一公式依然是解決問題的關鍵，但不同于原題中的直來直去，學生無法像原題那樣單憑數量等式去機械式地解決問題。此時，學生需要積極思考，去發現“每個月賣出的牛奶數量在增長”這一關鍵信息。如此一來，學生便能根據關鍵信息去思考“實際每個月牛奶的銷售數量”，繼而依據題中條件得出“實際每個月牛奶的銷售數量為132箱”，最終解決問題。

第三種是“對比變式”，教師可以在不改變題目結構和情境的基礎上，對原題的運算方法進行改變，將原題改為“超市新進了一批總重量不超過480千克的牛奶和餅干，已知牛奶的數量為40箱，每箱重量為10千克；一盒餅干的重量為7千克，則餅干的箱數是多少”？可以明顯看出，該變式題在運算方法上對學生提出了不同的要求，學生在計算完“480-40×10=80千克”后，需要利用“余數”來解決問題，這是在原題中沒有體現的內容。

總之，在間接變式下，習題會以另外一種面貌呈現在學生眼前，題中的信息變得更加復雜，但題目的本質并未發生改變，學生只需要積極調動自己的思維，充分地思考，那么所有的間接變式問題都能輕而易舉地解決。

三、開放變式，提升創新能力

創新能力作為小學數學十大核心素養之一，對于小學生的成長具有至關重要的作用。因此，在練習題的選擇上，教師可以進行針對性的變式訓練，來更好地幫助學生提升創新能力。通過研究發現，相比于封閉式習題，開放式習題更能有效鍛煉學生思維能力以及提升創新能力。教師應給予學生更多接觸開放式習題的機會，讓學生思維不斷活躍，促使他們不斷提升創新能力。

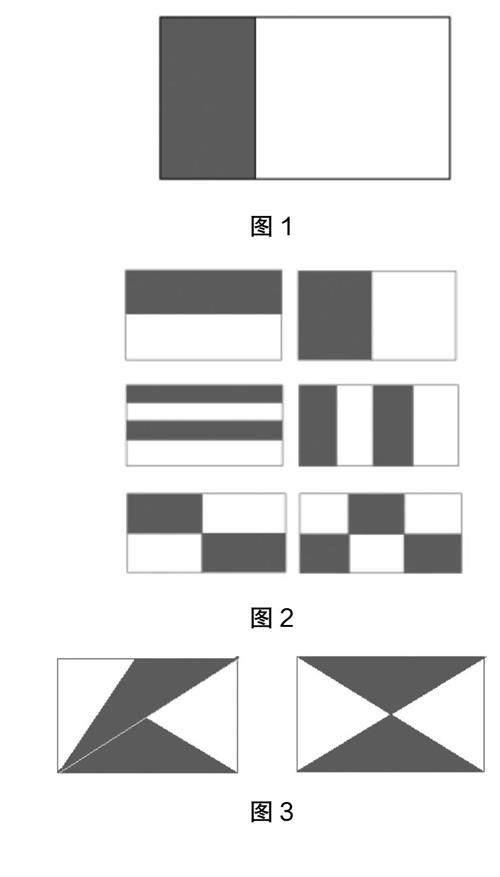
比如，教材中常常出現如下習題：已知有一塊長為6米、寬為4米的長方形園地，現要畫出一塊長為4米、寬為2米的區域來種植樹木（如圖1），則該區域的面積為多少？占整個長方形園地的幾分之幾？可以看出，這是一道非常簡單的分數類題目，適合學生初期學習，但并不能起到提升學生創新能力的作用。對此，教師不妨將此題目進行開放式處理，將原題改為：已知有一塊長為6米、寬為4米的長方形園地，現需要在該園地上開辟一塊區域來種植樹木，要求此區域的面積是園地面積的一半，該如何設計？在實際教學中可以發現，“沿著長方形橫向或者縱向進行對半畫線”是學生能快速想到的一種方法。除此之外，學生則一籌莫展。此時，教師可以進行點撥：“難不成只有將圖形一分為二這一種方法嗎？”經過思考，有的學生指出：“可以將長方形分為偶數個大小相同的小圖形，然后取出其中的一半。”在實際操作中，有的學生沿著長方形的縱向等距地畫出3條線段，從而得到4個大小相同的小長方形，最終挑選其中的2塊區域作為種樹區域；有的學生“依葫蘆畫瓢”，沿著長方形的橫向等距地畫出3條線段，也得到4個大小相等的小長方形。這時，教師需要繼續引導：“在這些方法中，不是單純地用豎線，就是純粹地使用橫線，大家有沒有其他想法呢？”通過質疑，有的學生想到了將橫線與豎線融合的方法，把長方形沿著縱向和橫向等距地各畫出1條線段，從而得到4個大小相等的圖形，最終選取其中的2塊區域即可（如圖2）。

隨著越來越多方法的出現，不斷激發學生的發散性思維；同時，可以驚喜地發現，有學生將三角形的知識融入此問題的解決思路中（如圖3所示）。總之，在實際教學過程中，教師要經常設計一些開放式的習題，幫助學生突破思維定式，讓學生大膽地提出自己內心的奇特想法，鼓勵學生“天馬行空”地想象［３］。時間長了，學生高階思維能力的養成以及創新能力的培養也將瓜熟蒂落、水到渠成。

四、綜合變式，發展綜合素養

小學數學知識本身的內在聯系是緊密的，是一個不可割裂的整體。因此，這就要求學生必須擁有掌控知識全局的能力。同時，從習題設計的角度來說，如果學生學習一個新的知識點，那么在練習的時候，教師不能總是單一地呈現和該知識點相關的習題，而應該在習題中有效融入一些與新知識點相關的知識與內容。這樣一來，學生既能熟練地掌握新知識，又能及時地鞏固舊知識，并且還能知曉兩者之間的聯系，真正起到融會貫通的良好效果，從而提升自身的綜合素養。

比如習題：現有一個用籬笆圍成的長方形菜園，已知菜園的長為6米，寬比長少2米，則長方形菜園的面積是多少？顯而易見，這是一道非常常規的“已知邊長求面積”類問題，只能承擔夯實學生基礎的作用，起不到提升學生綜合能力的效果。對此，教師可將原題改為：用一根長為24米的籬笆圍出一個長方形菜地，同時要求圍成的菜地盡可能大，那么長與寬分別是多少？此時長方形菜地的面積是多少？可以看出，此題既考查了學生對于周長的理解，也體現了學生對于面積的應用，甚至還包含了分類討論的思想。在實際練習中可以發現，大多數學生雖然能從題目中讀出“長方形的周長是24米”這一重要信息，但不能很好地利用“圍成的菜地盡可能大”這一條件。這時，教師便可稍加引導，讓學生知曉要根據周長來羅列出大小不同的長方形，最后得到面積最大的長方形。依據這個思路，學生羅列出“長為11米，寬為1米”“長為10米，寬為2米”等長方形，最終發現“長為6米，寬為6米”的正方形的面積最大。此時，教師可以根據習題的答案延伸問題：“答案所得的是什么圖形？如果籬笆的長為48米或60米，那么菜地的面積最大是多少？此時又是什么圖形？”學生帶著這些疑問，利用分類討論的思想，成功地得到了“在周長不變的情況下，圍成的正方形的面積大于所有的長方形的面積”這一結論。可以發現，在單一的習題變得綜合化后，學生需要考慮的問題變多了，用到的知識更廣了。可以預見的是，經過長期練習，學生必將能熟練地運用各種數學知識，最終提升自我的綜合能力。

總之，習題變式具有重要意義，其核心就是為了提升學生的創新能力和思維能力，最終更好地發展學生的素養。同時，變式題的數量不在多而在優，教師一定要遵循學生的心理特點，依據適度性原則設計出層次分明的變式題，讓學生在循序漸進的過程中獲得更好的發展。

參考文獻：

［１］ 施翠琴. 小學數學問題解決中的變式教學研究［Ｊ］. 寧波大學，２０１３.

［２］ 李強. 小學數學練習課變式教學存在的問題及策略研究［Ｊ］. 寧波大學，２０１８.

［３］ 馬啟健. 高階思維發展下中低年級習題變式的策略探究［Ｊ］. 教師，２０２１（０９）：４６－４７.