例談中學“有廣度”數學課堂的實施路徑

趙京波 宋婷婷 黃麗雨 袁瀅

【摘 要】構建“有廣度”的數學課堂是落實核心素養培養目標，構建高效數學課堂的有效措施。在中學數學課堂中，教師可以以大概念為視角，以大單元為載體，通過情境創設、任務驅動等方式進行教學，構建“有廣度”的數學課堂，促進學生形成良好的數學認知結構。

【關鍵詞】中學數學；有廣度；“三度”數學課堂；核心素養

【中圖分類號】G633.6? 【文獻標志碼】A? 【文章編號】1005-6009（2024）11-0015-04

【作者簡介】1.趙京波，海南師范大學（海口，571158）數據科學與智慧教育教育部重點實驗室副教授，碩士生導師；2.宋婷婷，北京師范大學海口附屬學校（海口，571158）教師；3.黃麗雨，海南師范大學（海口，571158）教師教育學院碩士研究生；4.袁瀅，海南師范大學（海口，571158）教師教育學院碩士研究生。

“有廣度”的數學課堂，是指以大概念為視角，以大單元為教學主導，對教學內容進行二次組織，使得數學知識之間具有更為緊密的邏輯關系，促進學生學習過程中正遷移的產生，便于學生形成良好的數學認知結構。［1］本文以核心素養導向下中學“有廣度”的數學課堂建構為研究對象，以“橢圓及其標準方程”教學為例，進一步研究實際課堂中如何有效地建構“有廣度”的數學課堂。

一、以大概念為視角，從宏觀、中觀、微觀三個層面分析課程內容

現有研究表明，要實現“有廣度”的數學課堂需要教師從整體的大框架上把握知識體系，對教學內容進行再次重構，并以大單元教學為教學手段，從多種維度深層次理解課程內容。這就需要教師將課程內容分為宏觀、中觀、微觀三個層次，從部分到整體，進一步厘清課程編排的體系，從而獲得更好的教學效果。［2］

以“幾何與代數”大概念為例，平面解析幾何作為其中的一個大單元，《普通高中數學課程標準（2017年版2020年修訂）》（以下簡稱“新課標”）將其劃分為“直線與方程”“圓與方程”“圓錐曲線與方程”和“平面解析幾何的形成與發展”四個部分。［3］宏觀上是運用平面解析幾何的方法學習直線、圓、圓錐曲線等的幾何特征。中觀上分為“直線和圓的方程”“圓錐曲線的方程”兩部分。微觀上首先通過直線的方程引入，探索直線的性質，接著學習直線的交點坐標與距離公式，從而利用兩點間的距離公式引出圓的標準方程，繼而探究直線與圓、圓與圓的位置關系。然后從圓的標準方程的推導類比到橢圓的標準方程的推導與雙曲線和拋物線的標準方程的推導，以及通過類比探究橢圓標準方程和幾何圖形之間的關系的方法來探究雙曲線和拋物線的標準方程和幾何圖形之間的關系。根據上述分析，筆者設置了以下學習目標：

1.通過觀察平面截圓錐，知道當平面與圓錐的軸所成的角變化時，截口曲線可以分別是圓、橢圓、雙曲線和拋物線；

2.掌握橢圓的定義、橢圓的標準方程，培養數學抽象素養；

3.通過橢圓標準方程的推導過程，培養學生發現問題、認識問題并利用規律解決問題的能力，提高邏輯推理能力。同時在橢圓的標準方程的推導運算中，培養數學運算、邏輯推理和數據分析素養；

4.熟練掌握橢圓的標準方程，能夠理解a，b，c的幾何意義，培養直觀想象素養。

二、以大單元為載體，創設具有“真實性”的問題情境

對課程內容進行大單元教學能夠讓學生對課程內容的層次和邏輯有更深入的理解，而這需要在數學課堂的問題情境中體現“真實性”。

具有“真實性”的問題情境是從現實世界中“捕獲”的真實問題和這一問題的情境脈絡，源自人們的生產生活實踐或科學研究活動。因其與學生的生活有著天然的關聯性，學生往往會被這些“我的問題”所吸引。學生數學核心素養的發展，關鍵在于通過在真實問題情境中的學習，培養其解決問題所需要的能力和個性品質。此外，“真實性”也是課程內容和現實世界連接的紐帶，能夠幫助學生理解課程內容在現實生活中的應用及作用。教師要善于創設真實的教學情境，將數學問題帶入真實的情境中幫助學生去理解知識，這樣可以達到事半功倍的效果。同時，真實的生活情境還可以拉近學生與數學的距離，讓學生對數學產生親切感，有效激發學生的學習興趣。

以“橢圓及其標準方程”教學為例，筆者以如下方式展開，以實現教學引入：

【問題1】用一個垂直于圓錐的軸的平面截圓錐，截口曲線（截面與圓錐側面的交線）是一個圓。如果改變截面與圓錐的軸所成的角，會得到怎樣的截口曲線呢？

師：用一個不垂直于圓錐的軸的平面截圓錐，當圓錐的軸與截面所成的角不同時，可以得到不同的截口曲線，它們分別是橢圓、拋物線和雙曲線。我們通常把橢圓、拋物線、雙曲線統稱為圓錐曲線。

然后教師再用信息技術展示行星繞太陽運行的軌跡、衛星接收天線、探照燈反射鏡面等，讓學生感受圓錐曲線在生產生活中的廣泛應用。

【問題2】類比直線和圓的方程的研究過程，你認為我們應按怎樣的路徑研究圓錐曲線？

學生經過自主思考和相互交流，類比直線和圓的方程的研究過程，得到圓錐曲線的研究路徑：現實背景（研究的必要性）—曲線的概念（建立曲線方程的依據）—曲線的方程（運用坐標法）—曲線的性質—實際應用。

上述教學是基于幾何與代數大概念下的“圓錐曲線”大單元教學，教師通過對圓錐不同角度切割得到不同的曲線為導入，引入橢圓的概念，并讓學生認識到圓錐曲線的類型，從而對橢圓既有微觀層面上的了解，也有宏觀層面上的把握，將“有廣度”的數學課堂落實到真實問題情境的創設中。

三、以問題為驅動，設置主題式探索教學過程，實現任務驅動

良好的問題情境可以獲得更好的教學效果，而對課程內容的教學過程可以嘗試進行主題式探索（創研式、對比式、挖井式、物聯式、穿越式、積淀式等），讓學生始終帶著“任務”去學習和思考，開展自主學習，確立任務驅動下的學習模式。“任務性”能夠讓學生帶著“任務”來學習，不斷深入思考，形式上可以是貫穿本單元內容的問題，也可以是貫穿幾個單元內容的問題。

以“橢圓及其標準方程”教學為例，在教授橢圓的概念和標準方程時，筆者設計了如下主題式探索教學過程。

1.橢圓的概念教學設計

【實驗操作】取一條定長的細繩，把它的兩端都固定在圖板的同一點，套上鉛筆，拉緊繩子，移動筆尖，這時筆尖（動點）畫出的軌跡是一個圓。如果把細繩的兩端拉開一段距離，分別固定在圖板的兩點上，套上鉛筆，拉緊繩子，移動筆尖，畫出的軌跡是什么曲線？

【問題3】在這一過程中，移動的筆尖（動點）滿足的幾何條件是什么？

【問題4】應該如何完善剛才對橢圓的定義？

教師給出橢圓定義：平面內到兩個定點F1，F2的距離的和等于常數（大于[F1F2]）的點的軌跡叫作橢圓。這兩個定點F1，F2叫作橢圓的焦點，兩焦點之間的距離叫作橢圓的焦距，焦距的一半稱為半焦距。橢圓的焦距為2c，點M與焦點F1，F2的距離的和為2a。

【問題5】橢圓定義中我們應該特別關注哪些要素？

【設計意圖】上述教學是基于核心素養下“問題串”設計，讓學生在大概念視角下，感悟橢圓的幾何特征，這是對課程內容微觀層面的把握，從而將“有廣度”的數學課堂落實到具體動手操作中。教學中引導學生以確定筆尖（動點）軌跡的幾何要素為基礎，讓學生經歷從不嚴謹到嚴謹的過程，逐步完善對橢圓幾何特征的理解，抽象出橢圓的概念，從而培養學生思維的嚴謹性和數學抽象素養。

2.橢圓的標準方程教學設計

【問題6】在了解橢圓的概念后，我們下一步應該研究什么？

【問題7】觀察橢圓的形狀，你認為怎樣建立坐標系能使所得的橢圓方程形式簡單？

師：從橢圓性質看，它既是軸對稱圖形，也是中心對稱圖形，而且過兩個焦點的直線是它的對稱軸，所以我們可以以經過橢圓兩焦點F1，F2的直線為[x]軸，線段[F1F2]的垂直平分線為[y]軸，建立平面直角坐標系xOy。（如圖1）

（圖1）

【問題8】如何用坐標表示橢圓上點所滿足的條件？

學生活動：設[Mx，y]是橢圓上任意一點，橢圓的焦距為[2cc>0]，那么焦點F1，F2的坐標分別為（-c，0），（c，0）。根據橢圓的定義，設點[M]與焦點F1，F2的距離的和為[2a]。由橢圓的定義可知，橢圓可看作點集[P=MMF1+MF2=2a]。因為[MF1=x+c2+y2]，[MF2=x-c2+y2]，所以[x+c2+y2 +x-c2+y2=2a]，化簡得：[x2a2+y2a2-c2=1]。

由橢圓的定義可知，[2a>2c>0]，即[a>c>0]，所以[a2-c2>0]。

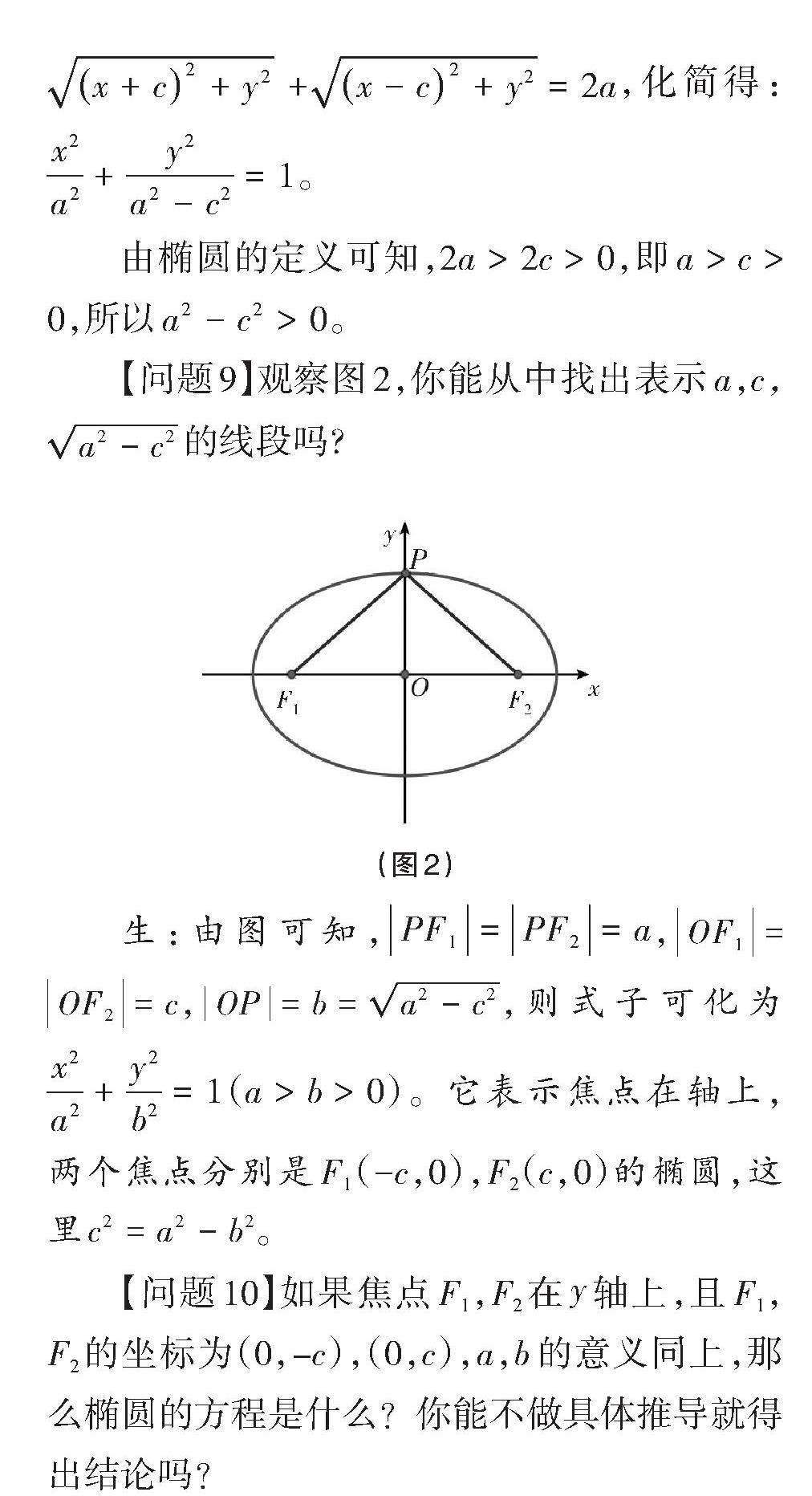
【問題9】觀察圖2，你能從中找出表示a，c，[a2-c2]的線段嗎？

（圖2）

生：由圖可知，[PF1=PF2=a]，[OF1=OF2=c]，[OP=b=a2-c2]，則式子可化為[x2a2+y2b2=1]（[a>b>0]）。它表示焦點在軸上，兩個焦點分別是F1（-c，0），F2（c，0）的橢圓，這里[c2=a2-b2]。

【問題10】如果焦點F1，F2在[y]軸上，且F1，F2的坐標為（0，-c），（0，c），a，b的意義同上，那么橢圓的方程是什么？你能不做具體推導就得出結論嗎？

【問題11】在橢圓中怎么區分焦點坐標在[x]軸還是[y]軸？

上述教學在探究橢圓的標準方程時利用挖井式的探究方法，通過不斷深入的問題一步步引導學生學會探究圓錐曲線的一般方法，并回憶圓的標準方程的推導過程：建系—設點—列式—化簡—證明，類比推理橢圓的標準方程。學生對方程中的a，b，c的幾何意義進行自主探索，并推導出焦點在[y]軸時橢圓的標準方程。整個過程都是在研究圓錐曲線的一般方法下進行的，這個研究方法同樣適用于雙曲線和拋物線，是在幾何與代數大概念視角下的教學設計。

本文以橢圓及其標準方程為例，展現了基于核心素養導向下“有廣度”的數學課堂的建構過程。“有廣度”的數學課堂對教師的專業素養要求較高，因此，作為數學教師需要不斷地鉆研數學教材，對教材進行再次理解和重構，在了解學生的基礎上選取最適宜的方式將知識教授給學生，達到最佳的教學效果。

【參考文獻】

［1］嚴虹.核心素養視閾下中小學“三度”數學課堂構建的一些思考［J］.數學通訊，2023（9）：6-9.

［2］李龍梅，嚴虹.核心素養視閾下中小學“三度”數學課堂構建的再思考［J］.興義民族師范學院學報，2023（4）：64-69.

［3］中華人民共和國教育部.普通高中數學課程標準（2017年版2020年修訂）［S］.北京：人民教育出版社，2020：43.