數(shù)學(xué)與音樂的跨學(xué)科融合

金奎 陳緒梅

【摘要】跨學(xué)科教學(xué)是新課標(biāo)重點(diǎn)倡導(dǎo)的教學(xué)方式.基于跨學(xué)科的教學(xué)視角，實(shí)現(xiàn)數(shù)學(xué)與音樂的融合，讓學(xué)生在體驗(yàn)音樂之美的過程中體會(huì)數(shù)學(xué)原理，運(yùn)用數(shù)學(xué)知識(shí)解決實(shí)際問題，培養(yǎng)其模型意識(shí)和應(yīng)用意識(shí)，關(guān)注學(xué)生創(chuàng)新意識(shí)的培養(yǎng).

【關(guān)鍵詞】跨學(xué)科；綜合與實(shí)踐；核心素養(yǎng)

1引言

《義務(wù)教育數(shù)學(xué)課程標(biāo)準(zhǔn)（2022 版）》（ 以下簡(jiǎn)稱《新課標(biāo)》）指出：綜合與實(shí)踐領(lǐng)域的教學(xué)活動(dòng)，以解決實(shí)際問題為重點(diǎn)，以跨學(xué)科主題式學(xué)習(xí)為主，適當(dāng)采取主題活動(dòng)或項(xiàng)目學(xué)習(xí)的方式呈現(xiàn)，通過綜合運(yùn)用數(shù)學(xué)和其他學(xué)科的知識(shí)與方法解決真實(shí)問題，著力培養(yǎng)學(xué)生的創(chuàng)新意識(shí)、實(shí)踐能力、社會(huì)擔(dān)當(dāng)?shù)染C合品質(zhì)[1].在跨學(xué)科情境項(xiàng)目化改造教學(xué)中，通過教師把握“度”的實(shí)踐教學(xué)指導(dǎo)，提高學(xué)生學(xué)習(xí)數(shù)學(xué)“悟”的真諦[2].本文以人教版九年級(jí)下冊(cè)“實(shí)際問題與反比例函數(shù) ”為例，設(shè)計(jì)和實(shí)施數(shù)學(xué)與音樂跨學(xué)科學(xué)習(xí)，結(jié)合具體情境體會(huì)反比例函數(shù)的意義，并能應(yīng)用反比例函數(shù)解決簡(jiǎn)單實(shí)際問題.2數(shù)學(xué)與音樂融合

從古至今，數(shù)學(xué)與音樂一直相輔相成.數(shù)學(xué)家畢達(dá)哥拉斯在世界上第一次發(fā)現(xiàn)音樂與數(shù)學(xué)的關(guān)系；中國(guó)古代通過數(shù)學(xué)運(yùn)算研究音律；萊布尼茨說(shuō)音樂是一種隱藏的數(shù)學(xué)練習(xí)；傅里葉發(fā)現(xiàn)聲波是周期函數(shù)的一種；音樂大師貝多芬、肖邦、柴可夫斯基等也常常根據(jù)曲線來(lái)譜曲.

音樂離不開數(shù)學(xué)思維，數(shù)學(xué)思維的秩序性可以讓音樂呈現(xiàn)出節(jié)奏、穩(wěn)定、有序的狀態(tài)，能夠使聽眾產(chǎn)生和諧、愉悅的感受.數(shù)學(xué)的思維方式不僅能夠讓學(xué)生更好地理解音樂，鑒賞音樂，也能幫助學(xué)生用理性邏輯創(chuàng)作音樂.在我國(guó)最早產(chǎn)生的完備的律學(xué)理論是三分損益律，時(shí)間大約在春秋中期，《管子·地員篇》和《呂氏春秋·音律篇》中分別有述；明代朱載 （1536—1610）在其音樂著作《律學(xué)新說(shuō)》對(duì)十二平均律的計(jì)算方法作了概述，在《律呂精義·內(nèi)篇》中對(duì)十二平均律理論作了論述，并把十二平均律計(jì)算的十分精確，與當(dāng)今的十二平均律完全相同，這在世界上屬于首次[3]．根據(jù)十二平均律的定義，也可以寫為數(shù)字式，如：122·122·122·…=2.因此，相鄰的兩個(gè)音之間的頻率比為fn[]fn-1=122=1.05946…由此可見，在古代音樂的發(fā)展就與數(shù)學(xué)緊密地聯(lián)系在了一起.從那時(shí)起，隨著數(shù)學(xué)和音樂的不斷發(fā)展，人們對(duì)它們之間關(guān)系的理解和認(rèn)識(shí)也在不斷地加深.

3教學(xué)過程

3.1設(shè)境催問，引燃探究

讓學(xué)生用吸管吹奏音樂，感受吸管長(zhǎng)度不同，吹出的音調(diào)也不同.引導(dǎo)學(xué)生從音樂、科學(xué)、物理等相關(guān)知識(shí)進(jìn)行思考，從其他學(xué)科引入數(shù)學(xué)問題，然后運(yùn)用數(shù)學(xué)加以解決，這始終是數(shù)學(xué)學(xué)習(xí)的重要方法.學(xué)生已了解到音調(diào)與吸管材質(zhì)、吸管粗細(xì)、吸管長(zhǎng)度、吹氣的力度等有關(guān).本節(jié)課在吸管材質(zhì)和粗細(xì)均相同條件下，聚焦到音調(diào)和吸管長(zhǎng)度的關(guān)系.

本節(jié)課基于音樂常識(shí)（吸管越短，音調(diào)越高）、物理常識(shí)（吸管越短，振動(dòng)頻率越大），通過信息技術(shù)軟件（Phyphox和Geogebra軟件）輔助，建立數(shù)學(xué)模型，讓學(xué)生在真實(shí)的環(huán)境中探索，應(yīng)用數(shù)學(xué)知識(shí)發(fā)現(xiàn)、解決問題，提升學(xué)生思維品質(zhì).

在課堂開始之前，請(qǐng)學(xué)生們來(lái)欣賞一段音樂.（播放吹吸管音樂）

問題1他們?cè)谟檬裁礃菲餮葑啵?/p>

師生活動(dòng)學(xué)生通過觀看視頻，回答樂曲是用吸管吹奏的.

問題2吹吸管能發(fā)出聲音嗎？

師生活動(dòng)學(xué)生體驗(yàn)吹吸管能發(fā)出聲音，確定本研究的可操作性.

問題3如何吹出不同的音調(diào)？和哪些因素有關(guān)？

師生活動(dòng)學(xué)生根據(jù)音樂、物理等相關(guān)知識(shí)進(jìn)行發(fā)散性思維，讓學(xué)生自由發(fā)揮，充分調(diào)動(dòng)學(xué)生積極性和求知欲，通過教師的引導(dǎo)，讓學(xué)生發(fā)現(xiàn)問題，進(jìn)行自我總結(jié)和反思，培養(yǎng)學(xué)生的批判精神.最終得出音調(diào)與吸管材質(zhì)、吸管粗細(xì)、吹氣的力度、吸管長(zhǎng)度等有關(guān)，本節(jié)將問題聚焦到音調(diào)與吸管長(zhǎng)度的關(guān)系.

問題4改變吸管長(zhǎng)度真的能吹出不同的音調(diào)嗎？

師生活動(dòng)學(xué)生現(xiàn)場(chǎng)操作，同桌相互配合，一人吹、另一人剪，并邀請(qǐng)兩位同學(xué)上臺(tái)展示.實(shí)驗(yàn)發(fā)現(xiàn)：吸管越短，音調(diào)越高.學(xué)生積極參與，共同探索它們的數(shù)量關(guān)系和變化規(guī)律.

設(shè)計(jì)意圖本節(jié)從優(yōu)美的音樂入手，感受音樂之美和中國(guó)傳統(tǒng)文化的博大精深.涉及一些音樂與物理的知識(shí)，學(xué)生在理解上存在一定的難度.通過問題，將數(shù)學(xué)和其他學(xué)科的知識(shí)整合起來(lái)，側(cè)重幫助學(xué)生深入學(xué)習(xí)數(shù)學(xué)的知識(shí)和技能、理解數(shù)學(xué)的思想和方法，能創(chuàng)造性地解決應(yīng)用性問題，實(shí)現(xiàn)跨學(xué)科教學(xué)[4].師生明確本節(jié)研究的對(duì)象與任務(wù)，從變量角度進(jìn)一步加深對(duì)函數(shù)的認(rèn)識(shí)，引導(dǎo)學(xué)生運(yùn)用函數(shù)關(guān)系進(jìn)行分析.

3.2收集數(shù)據(jù)，建立模型

問題5如何研究?jī)蓚€(gè)變量之間的關(guān)系？

追問1用函數(shù)來(lái)研究?jī)烧咧g的關(guān)系，具體應(yīng)該怎么做呢？

追問2收集什么數(shù)據(jù)？

師生活動(dòng)師生共同確定好變量，確定用函數(shù)來(lái)研究此問題，可運(yùn)用刻度尺測(cè)出吸管的長(zhǎng)度，用Phyphox軟件測(cè)量出此長(zhǎng)度下吹吸管的振動(dòng)頻率（圖1、圖2）.

（學(xué)生現(xiàn)場(chǎng)實(shí)驗(yàn)，前后四人互為一組，在小組內(nèi)一人吹吸管，一人測(cè)量振動(dòng)頻率，一人讀取數(shù)據(jù)，一人將數(shù)據(jù)記錄在數(shù)學(xué)實(shí)驗(yàn)報(bào)告單中.）

問題6要想通過實(shí)驗(yàn)得出有用的數(shù)據(jù)，在實(shí)驗(yàn)之前需要思考怎樣做，以及會(huì)遇到哪些問題.同時(shí)，在這次測(cè)量活動(dòng)中我們要對(duì)同學(xué)們的表現(xiàn)進(jìn)行評(píng)價(jià)，評(píng)比出最佳測(cè)量小組.你認(rèn)為需要圍繞哪些方面進(jìn)行評(píng)價(jià)呢？

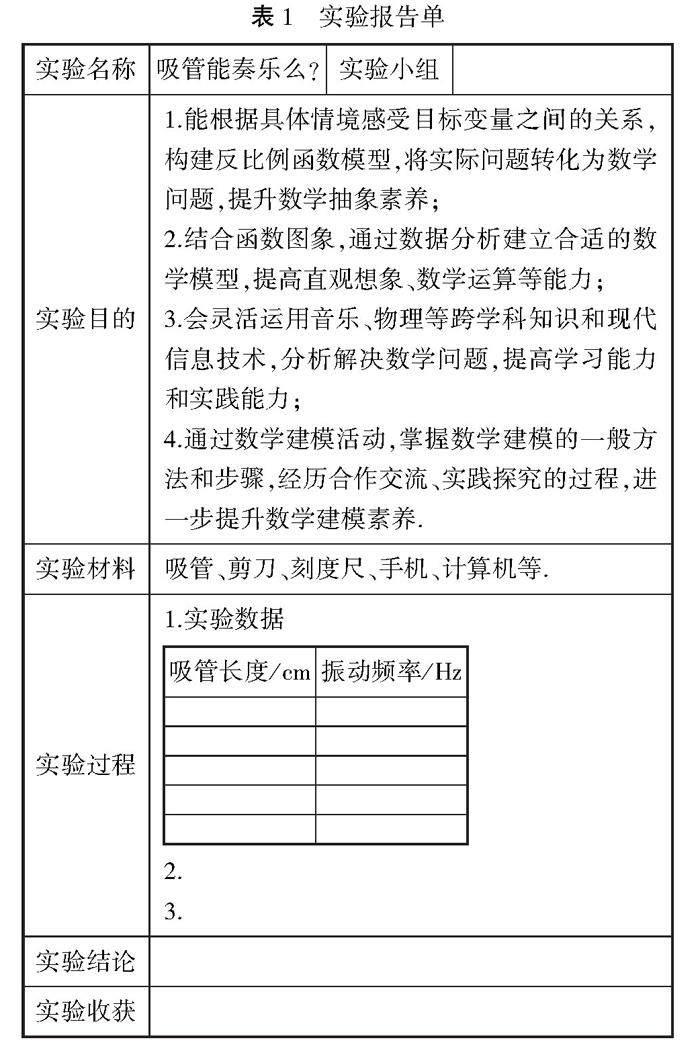
師生活動(dòng)師生共同制定實(shí)驗(yàn)報(bào)告單（表1）和實(shí)驗(yàn)評(píng)價(jià)表（表2），學(xué)生在教師的引導(dǎo)下動(dòng)手完成實(shí)驗(yàn)，按照項(xiàng)目化的分工，一部分學(xué)生記錄數(shù)據(jù)，一部分學(xué)生統(tǒng)計(jì)數(shù)據(jù)，一部分學(xué)生協(xié)助，合作完成實(shí)驗(yàn)報(bào)告單和評(píng)價(jià)表.

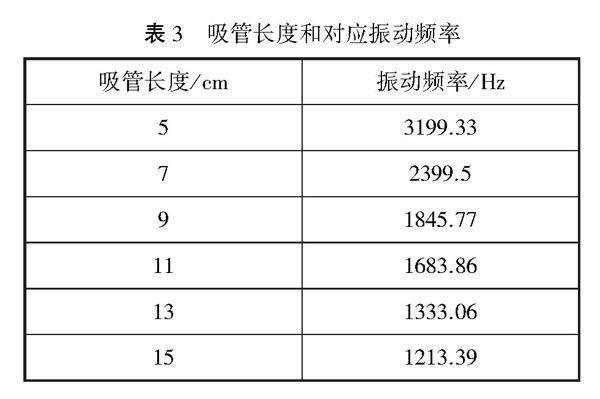
追問1：要更直觀地表示這組數(shù)據(jù)的變化規(guī)律（如上表3），有什么方法？

追問2：觀察圖象，可以用什么函數(shù)來(lái)刻畫兩個(gè)變量之間的關(guān)系？

師生活動(dòng)1.教師提出問題，學(xué)生獨(dú)立解決問題.學(xué)生畫出圖象后，發(fā)現(xiàn)有的圖象接近于一次函數(shù)，有的接近于反比例函數(shù).經(jīng)過反復(fù)實(shí)驗(yàn)，多次得到數(shù)據(jù)，畫出圖象，猜測(cè)更接近于反比例函數(shù).教師巡視學(xué)生完成情況，并請(qǐng)學(xué)生展示解答過程（圖3），給予適當(dāng)評(píng)價(jià).2.師生共同分析數(shù)據(jù)，引導(dǎo)學(xué)生經(jīng)歷觀察表格、尋找規(guī)律、描點(diǎn)繪圖、觀察圖象的過程.由于手動(dòng)繪圖存在一定的誤差，教師引導(dǎo)學(xué)生運(yùn)用現(xiàn)代信息技術(shù)（如Geogebra軟件），幫助學(xué)生利用已學(xué)的函數(shù)圖象與性質(zhì)，確定函數(shù)更接近于反比例函數(shù)（圖4），即可以選擇反比例函數(shù)來(lái)刻畫這兩個(gè)變量之間的關(guān)系，擬合得到函數(shù)表達(dá)式.

教學(xué)說(shuō)明《新課標(biāo)》指出：模型思想的建立是學(xué)生體會(huì)和理解數(shù)學(xué)與外部世界聯(lián)系的基本途徑.學(xué)生根據(jù)已學(xué)物理知識(shí)將音樂中抽象的音調(diào)轉(zhuǎn)化為可以測(cè)量的振動(dòng)頻率這一想法，筆者給予了高度的贊賞.《新課標(biāo)》指出：數(shù)學(xué)教學(xué)應(yīng)該從學(xué)生已有的生活經(jīng)驗(yàn)出發(fā)，讓學(xué)生親身經(jīng)歷將實(shí)際問題抽象成數(shù)學(xué)模型并理解運(yùn)用的過程.本節(jié)活動(dòng)課的設(shè)計(jì)體現(xiàn)綜合與實(shí)踐課從生活出發(fā)、學(xué)科融合的特質(zhì).

設(shè)計(jì)意圖引導(dǎo)學(xué)生通過實(shí)驗(yàn)收集數(shù)據(jù)，從觀察表格數(shù)據(jù)發(fā)現(xiàn)規(guī)律過渡到繪制函數(shù)圖象，使學(xué)

生經(jīng)歷將現(xiàn)實(shí)問題轉(zhuǎn)化為數(shù)學(xué)問題的過程.Geogebra軟件的應(yīng)用讓學(xué)生體會(huì)到信息技術(shù)在數(shù)學(xué)建模

中的作用，引導(dǎo)學(xué)生經(jīng)歷“看數(shù)據(jù)，繪圖象，先猜想，再判斷”的過程，滲透數(shù)形結(jié)合的思想，為

應(yīng)用函數(shù)模型打好基礎(chǔ).

3.3應(yīng)用模型，成果展示

問題8吸管長(zhǎng)度5cm，對(duì)應(yīng)的振動(dòng)頻率是多少呢？

師生活動(dòng)依據(jù)圖4，總結(jié)求出解析式，正確使用反比例函數(shù)解析式解決問題，得到應(yīng)使用長(zhǎng)度的吸管.教師可以利用Geogebra軟件操作驗(yàn)證得到圖5，并請(qǐng)另一位學(xué)生進(jìn)行實(shí)驗(yàn)驗(yàn)證.

問題9嘗試完成《小星星》的吹奏并進(jìn)行成果展示.

設(shè)計(jì)意圖通過具體情境應(yīng)用反比例函數(shù)模型解決問題，對(duì)反比例函數(shù)的性質(zhì)和圖象等有更深入的理解.小組合作吹奏歌曲《小星星》，學(xué)生經(jīng)歷合作交流、實(shí)踐探索和組織協(xié)調(diào)的過程，親身動(dòng)手、

動(dòng)腦、動(dòng)嘴，充分感受數(shù)學(xué)與音樂的緊密融合，發(fā)展學(xué)習(xí)能力和實(shí)踐能力.

3.4問題歸納，課堂小結(jié)

（1）回顧探索音調(diào)與吸管長(zhǎng)度關(guān)系的過程，我們經(jīng)歷了哪些步驟？

師生活動(dòng)：學(xué)生先自己總結(jié)，進(jìn)行交流互動(dòng)，再得出數(shù)學(xué)建模的一般步驟，由實(shí)驗(yàn)獲得數(shù)據(jù)—用描點(diǎn)法畫出圖象—根據(jù)圖象選擇函數(shù)—擬合求函數(shù)關(guān)系式—應(yīng)用模型解決問題.

（2）經(jīng)過這一節(jié)課的學(xué)習(xí)，你有什么收獲？

師生活動(dòng)學(xué)生暢所欲言.

學(xué)生1我經(jīng)歷了整個(gè)數(shù)學(xué)建模過程，解決了音調(diào)與吸管長(zhǎng)度的關(guān)系問題.

學(xué)生2我感受到了高科技的魅力，比如用聲學(xué)軟件測(cè)頻率、計(jì)算機(jī)描點(diǎn)等.

學(xué)生3我感受到數(shù)學(xué)來(lái)源于生活，在日常生活中數(shù)學(xué)無(wú)處不在.

學(xué)生4我了解運(yùn)用函數(shù)解決問題的步驟：實(shí)驗(yàn)—收集數(shù)據(jù)—確定變量—描點(diǎn)—求函數(shù)解析式—評(píng)價(jià).

設(shè)計(jì)意圖由學(xué)生先自行整理回顧數(shù)學(xué)建模的全過程，明確數(shù)學(xué)建模的一般方法與步驟，再由教師補(bǔ)充提升，充分發(fā)揮了學(xué)生的自主性.通過對(duì)數(shù)學(xué)與音樂史的講述，感受數(shù)學(xué)與生活的緊密聯(lián)系，從情感上提升學(xué)生對(duì)數(shù)學(xué)學(xué)習(xí)的熱情.通過學(xué)生自行總結(jié)，檢驗(yàn)本節(jié)的教學(xué)效果，為今后的項(xiàng)目化的學(xué)習(xí)做好鋪墊.

3.5課后拓展，鞏固提升

（1）請(qǐng)選擇除吸管外的物品（如皮筋）對(duì)其音調(diào)與長(zhǎng)度的關(guān)系進(jìn)行探究，運(yùn)用數(shù)學(xué)建模的方法，尋找變量之間的關(guān)系，擬合函數(shù)，并應(yīng)用求得的函數(shù)自制樂器，完成樂曲的演奏.

（2）請(qǐng)考慮幾何結(jié)構(gòu)等因素，優(yōu)化自制樂器.

4教學(xué)感悟

4.1培養(yǎng)學(xué)生動(dòng)手實(shí)驗(yàn)?zāi)芰?/p>

杜威說(shuō)：“人們最初的知識(shí)，最能永久不忘的知識(shí)是關(guān)于‘怎樣做的知識(shí).”目前的一線數(shù)學(xué)教學(xué)中基本都以傳授知識(shí)為主的教學(xué)方式，為知識(shí)而講解知識(shí)，陷入學(xué)生死記硬背、盲目機(jī)械刷題、疲于應(yīng)付形形色色考試怪圈，完全扼殺學(xué)生動(dòng)手能力，忽略其知識(shí)生成的過程和本質(zhì)原理，無(wú)法提升學(xué)生思維能力和運(yùn)用數(shù)學(xué)知識(shí)解決實(shí)際問題的能力.

本節(jié)課從“做實(shí)驗(yàn)”的視角，通過學(xué)生親自參與，協(xié)同合作，在反復(fù)實(shí)驗(yàn)中，不斷修正，建立數(shù)學(xué)模型，積極評(píng)價(jià)，最大化地實(shí)現(xiàn)教學(xué)目標(biāo).通過數(shù)學(xué)與音樂的融合，讓學(xué)生親自參與，提高動(dòng)手能力，感受數(shù)學(xué)之美，感受生活中數(shù)學(xué)無(wú)處不在，提升學(xué)生核心素養(yǎng).

4.2培養(yǎng)學(xué)生解決問題的能力

讓學(xué)生在欣賞數(shù)學(xué)美、創(chuàng)造數(shù)學(xué)美的過程中，引發(fā)對(duì)數(shù)學(xué)文化的思考，培養(yǎng)學(xué)生運(yùn)用數(shù)學(xué)解決問題的能力[5].學(xué)生通過吸管實(shí)驗(yàn)，直觀感受音調(diào)與吸管長(zhǎng)度的關(guān)系，以振動(dòng)頻率與吸管長(zhǎng)度為變量建立數(shù)學(xué)模型，尋找數(shù)學(xué)關(guān)系，反復(fù)實(shí)驗(yàn)，收集數(shù)據(jù)，運(yùn)用信息技術(shù)處理數(shù)據(jù)，應(yīng)用數(shù)學(xué)知識(shí)處理圖象，構(gòu)建反比例函數(shù)模型，合理進(jìn)行評(píng)價(jià).

學(xué)生通過操作、驗(yàn)證、說(shuō)理，將零散的知識(shí)結(jié)構(gòu)化、單一的圖形模型化、抽象的思維顯性化、靜態(tài)的圖形動(dòng)態(tài)化，關(guān)注學(xué)科間的綜合聯(lián)系，形成對(duì)知識(shí)的整體性認(rèn)識(shí)，經(jīng)歷構(gòu)建反比例函數(shù)模型的探究過程.通過項(xiàng)目化學(xué)習(xí)，學(xué)生在不斷解決問題的過程中，體會(huì)如何利用理論知識(shí)解決問題的過程，從而在構(gòu)建反比例函數(shù)模型時(shí)，利用理論知識(shí)來(lái)尋找解決問題的基本方向，再進(jìn)一步利用知識(shí)指導(dǎo)實(shí)踐.學(xué)生在做中思，在思中行.

4.3培養(yǎng)學(xué)生批判性思維

《新課標(biāo)》明確要求：發(fā)展質(zhì)疑問難的批判性思維，形成實(shí)事求是的科學(xué)態(tài)度，初步養(yǎng)成講道理、有條理的思維品質(zhì)，逐步形成理性精神.目前課堂教學(xué)中，多數(shù)學(xué)生是老師要求做啥我就做啥，教材如何寫我就如何做，知其然不知其所以然，教師以教學(xué)時(shí)間不夠、學(xué)生能力差等為托詞，在課堂教學(xué)中忽視對(duì)學(xué)生批判性思維能力的培養(yǎng).教師要能自覺開發(fā)資源，并結(jié)合學(xué)生實(shí)際創(chuàng)設(shè)真實(shí)情境，深度挖掘蘊(yùn)含的培養(yǎng)批判性思維的價(jià)值，從問題處進(jìn)行批判性思考，從困惑處進(jìn)行批判性探索，從猜想處進(jìn)行批判性實(shí)驗(yàn)，從結(jié)論處進(jìn)行批判性驗(yàn)證，從遷移處進(jìn)行批判性拓展，引導(dǎo)學(xué)生領(lǐng)悟具有批判性學(xué)習(xí)的數(shù)學(xué)，從而促進(jìn)學(xué)生批判精神和批判能力的提升.

4.4跨學(xué)科教學(xué)的必要性

《新課標(biāo)》指出：義務(wù)教育的“綜合與實(shí)踐”以“跨學(xué)科主題學(xué)習(xí)”為主，其中小學(xué)可采用“主題活動(dòng)”和“項(xiàng)目式學(xué)習(xí)”，初中可采用“項(xiàng)目學(xué)習(xí)”，高中階段采取“數(shù)學(xué)建模活動(dòng)”與“數(shù)學(xué)探究活動(dòng)”[6].數(shù)學(xué)跨學(xué)科教學(xué)體現(xiàn)數(shù)學(xué)與其他學(xué)科的聯(lián)系，通過解決綜合性的實(shí)際問題，培養(yǎng)學(xué)生的模型觀念、數(shù)據(jù)分析意識(shí)、運(yùn)算能力和推理能力.跨學(xué)科除了教學(xué)內(nèi)容、教學(xué)形式的整合，更需要學(xué)生思維的整合，優(yōu)化并提升學(xué)生的思維品質(zhì).在課堂教學(xué)中引導(dǎo)學(xué)生在跨學(xué)科的背景下用數(shù)學(xué)的眼光觀察現(xiàn)實(shí)世界，用數(shù)學(xué)的語(yǔ)言表達(dá)現(xiàn)實(shí)世界中事物的概念、關(guān)系和規(guī)律，幫助學(xué)生感悟數(shù)學(xué)與現(xiàn)實(shí)世界的聯(lián)系[7].傳統(tǒng)教學(xué)中，由于缺失了對(duì)函數(shù)生成過程的展現(xiàn)，使得學(xué)生普遍認(rèn)為函數(shù)知識(shí)抽象難懂.本文借助跨學(xué)科的數(shù)學(xué)實(shí)驗(yàn)，讓學(xué)生經(jīng)歷了構(gòu)建函數(shù)的過程，深化了對(duì)函數(shù)概念的理解.

參考文獻(xiàn)

[1]中華人民共和國(guó)教育部.義務(wù)教育數(shù)學(xué)課程標(biāo)準(zhǔn)：2022年版[M].北京：北京師范大學(xué)出版社，2022：87.

[2]張潔，戴小駒，黃麗.跨學(xué)科情境教學(xué)：數(shù)學(xué)課堂的項(xiàng)目化改造：以“孟德爾遺傳規(guī)律”為例[J].中學(xué)數(shù)學(xué)月刊，2023（06）：43-46.

[3]劉衛(wèi)峰，王尚志.數(shù)學(xué)與音樂[J].數(shù)學(xué)通報(bào)，2005（04）：19-21.

[4]劉祖希.關(guān)于數(shù)學(xué)跨學(xué)科內(nèi)容與教學(xué)的已有研究：兼及2022年全國(guó)高考數(shù)學(xué)試卷跨學(xué)科試題分析[J].教育研究與評(píng)論（中學(xué)教育教學(xué)），2022（12）：5-11.

[5]肖丹，杜蘭歌，朱哲.數(shù)學(xué)與藝術(shù)的跨學(xué)科融合：以綜合與實(shí)踐課“美麗的鑲嵌”為例[J].中學(xué)數(shù)學(xué)月刊，2023（04）：41-43.

[6]劉祖希.圖說(shuō)數(shù)學(xué)與跨學(xué)科教學(xué)[J].中學(xué)數(shù)學(xué)雜志，2023（10）：19-20.

[7]中華人民共和國(guó)教育部.義務(wù)教育數(shù)學(xué)課程標(biāo)準(zhǔn)：2022年版[M].北京：北京師范大學(xué)出版社，2022：5.

作者簡(jiǎn)介金奎（1980—），男，安徽安慶人，蕪湖市中學(xué)數(shù)學(xué)教研員，安徽師范大學(xué)碩士研究生導(dǎo)師，蕪湖市數(shù)學(xué)學(xué)科帶頭人；出版著作兩本，主持多項(xiàng)省、市級(jí)課題，發(fā)表文章20余篇.

陳緒梅（1991—），女，安徽蕪湖人，中學(xué)二級(jí)教師；參與多項(xiàng)市級(jí)課題，獲蕪湖市中小學(xué)實(shí)驗(yàn)說(shuō)課一等獎(jiǎng).

基金項(xiàng)目

安徽省教育科學(xué)研究課題“多學(xué)段融通視域下數(shù)學(xué)閱讀課程資源的開發(fā)與實(shí)踐”（JK23176）.