折出60°的角

陶瓊

折紙做60°、30°、15°等特殊角是在學(xué)生學(xué)習(xí)了“三角形”“四邊形”“軸對(duì)稱”等基本概念、性質(zhì)的基礎(chǔ)上，進(jìn)一步研究圖形翻折的一次數(shù)學(xué)活動(dòng)。在此之前，教材已呈現(xiàn)折角平分線，折紙研究軸對(duì)稱圖形特點(diǎn)、全等圖形性質(zhì)等活動(dòng)。折紙有助于學(xué)生體會(huì)研究圖形性質(zhì)實(shí)際上就是揭示圖形中各幾何要素之間的關(guān)系，明確觀察、實(shí)驗(yàn)、猜想、證明是幾何研究的基本活動(dòng)，感悟“用合情推理發(fā)現(xiàn)結(jié)論，用演繹推理證明結(jié)論”這一幾何研究的基本思考方式。本節(jié)課的教學(xué)重點(diǎn)是用不同的方法折出60°的角并說明理由，有了60°的角，再通過對(duì)折得到30°、15°的角。

一、視頻導(dǎo)入，創(chuàng)設(shè)折紙情境

教學(xué)伊始，筆者讓學(xué)生思考不借助任何測(cè)量工具，在一張矩形紙片上折出一個(gè)正方形的方法，隨后播放演示視頻，讓學(xué)生觀察折的過程中，折出了多少度的角。學(xué)生觀看視頻后，都能發(fā)現(xiàn)折出了45°角。筆者順勢(shì)鼓勵(lì)學(xué)生動(dòng)手折一折，大部分學(xué)生都能將矩形沿著對(duì)角線對(duì)折，很快折出45°角。筆者肯定了學(xué)生折45°角的方法，并在用幾何畫板演示折角過程后追問：如圖1所示，哪些角等于45°？你還發(fā)現(xiàn)了哪些度數(shù)的角？折痕AE可以看作對(duì)稱點(diǎn)B與B'的什么？折疊前后的兩個(gè)對(duì)應(yīng)圖形有什么關(guān)系？

學(xué)生很快發(fā)現(xiàn)：∠BAE、∠EAD、∠AEB、∠AEB'都等于45°；計(jì)算得到∠AEC=135°；折痕AE可以看作B與B'的對(duì)稱軸；折疊前后兩個(gè)圖形全等。

45°角的折法讓學(xué)生識(shí)別出折痕的本質(zhì)，意識(shí)到對(duì)折可以平分一個(gè)角。最后，筆者追問：按照同樣的方法，你還可以折出哪些角呢？有了剛才折45°角的活動(dòng)經(jīng)驗(yàn)，學(xué)生很快通過對(duì)折折出了22.5°，11.25°等“倍分”的角，為后面折出60°角后對(duì)折得出30°、15°的角做鋪墊。

二、設(shè)置問題支架，引導(dǎo)動(dòng)手操作

教學(xué)中，筆者設(shè)計(jì)主問題：能不能像折45°角那樣，不借助任何測(cè)量工具，僅用一張矩形紙片準(zhǔn)確地折出60°角呢？折60°角對(duì)學(xué)生而言難度比較大，筆者通過設(shè)置問題支架，引導(dǎo)學(xué)生動(dòng)手操作。

問題支架1：我們學(xué)過的什么圖形里有60°角呢？

在已學(xué)的特殊三角形中，學(xué)生想到等邊三角形和有30°角的直角三角形里有60°角，從而打開了思路。

問題支架2（思路一）：如何用一個(gè)矩形紙片折一個(gè)等邊三角形呢？

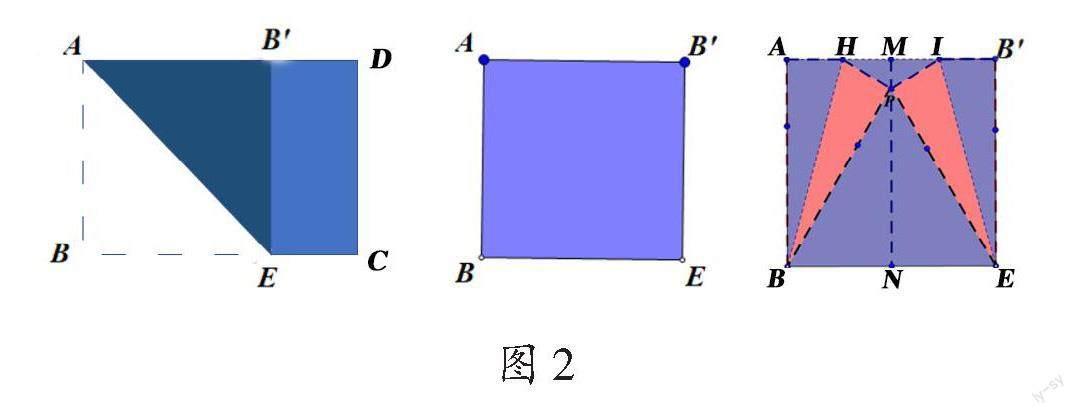
筆者引導(dǎo)學(xué)生回想剛才折45°角的過程：我們可以折出一個(gè)正方形，得到4條相等的邊。學(xué)生順勢(shì)思考如何讓正方形4條邊中任意3條“聚”在一個(gè)三角形里，進(jìn)而折出等邊三角形，得到60°角。學(xué)生嘗試折紙后展示折法，筆者用多媒體演示折疊過程（如圖2）。

問題支架3（思路二）：我們將圖2中的正方形沿著折痕MN對(duì)折，觀察圖形（如圖3），此時(shí)∠PEN還等于60°嗎？PE和EN有什么數(shù)量關(guān)系？

學(xué)生回答：∠PEN仍然等于60°，PE=2EN。接著，筆者引導(dǎo)學(xué)生分析：∠PNE=90°和PE=2EN是因，∠PEN=60°是果，并讓學(xué)生證明。

學(xué)生根據(jù)之前學(xué)習(xí)的特殊四邊形以及直角三角形的性質(zhì)等，很快證出這個(gè)推論。接著，學(xué)生嘗試折紙，小組交流合作，構(gòu)造斜邊是直角邊2倍的三角形。

折法一：（如圖4）對(duì)折矩形ABCD，使AD與BC重合，得到折痕EF，把紙片展平，再一次折疊紙片，使點(diǎn)A落在EF上，并使折痕經(jīng)過點(diǎn)B，得到折痕BM，同時(shí)得到線段BN。

筆者追問：觀察折痕EF與AB的關(guān)系，你還有其他證法嗎？寫出已知、求證，并完成證明。學(xué)生寫出“已知：如圖5，在矩形ABCD中，EF垂直平分AB，△ABM與△NBM關(guān)于BM軸對(duì)稱，點(diǎn)N在EF上。求證：∠ABN=60°”。學(xué)生識(shí)別出折痕的本質(zhì)就是對(duì)稱軸，想到EF是AB的垂直平分線，于是想到連接AN（如圖5）。

學(xué)生上講臺(tái)板書證明過程：連接AN，因?yàn)镋F垂直平分AB，所以AN＝BN；又因?yàn)椤鰽BM與△NBM關(guān)于BM軸對(duì)稱，所以AB=BN；可得AB＝BN=AN，△ABN是等邊三角形，所以∠ABN＝60°。

筆者繼續(xù)追問：剛才的折紙過程是將矩形紙片對(duì)折一次，如果對(duì)折兩次，你還可以折出60°角嗎？學(xué)生先獨(dú)立思考，設(shè)計(jì)方案，解決問題，再在小組中交流自己的折法。學(xué)生上講臺(tái)展示折法，筆者用多媒體演示折疊過程。

折法二：（如圖6）將矩形紙片對(duì)折兩次，得到三條折痕，分別為MN、EF、GH，再一次翻折，使點(diǎn)B落在MN上，并使折痕經(jīng)過點(diǎn)E，從而得到∠AEB′＝60°。

筆者通過折紙活動(dòng)，讓學(xué)生經(jīng)歷思考、操作、觀察、猜想、驗(yàn)證的活動(dòng)過程，體會(huì)到轉(zhuǎn)化思想。不同折法讓學(xué)生體驗(yàn)到方法的靈活性，用不同方法證明折法的過程培養(yǎng)了學(xué)生的創(chuàng)新思維。

問題支架4：同學(xué)們已經(jīng)學(xué)會(huì)了折60°角，你能折出30°、15°角嗎？你還能折出其他度數(shù)的角嗎？

通過小組交流，學(xué)生認(rèn)識(shí)到通過對(duì)折可以得到60°角的“倍分”角，進(jìn)一步體會(huì)到對(duì)折的實(shí)質(zhì)是軸對(duì)稱，可以將角平分，繼而得到“和差、倍分”的角。

三、拓展鞏固，積累數(shù)學(xué)活動(dòng)經(jīng)驗(yàn)

為幫助學(xué)生積累數(shù)學(xué)活動(dòng)經(jīng)驗(yàn)，筆者先讓學(xué)生歸納、梳理本節(jié)課中用矩形紙片折出了哪些特殊度數(shù)的角，如何折出60°的角，具體用到了哪些知識(shí)；再出示由易到難的三類練習(xí)題。

【基礎(chǔ)性練習(xí)】如圖7，把一個(gè)正方形的紙片對(duì)折兩次，然后剪下一個(gè)角。要得到一個(gè)正方形，剪口與折痕應(yīng)成多少度角？

【鞏固性練習(xí)】如圖8，樂樂用一張長方形紙片折紙飛機(jī)，折疊過程如圖8所示，則∠ACB的度數(shù)為 ?????? 。

【提高性練習(xí)】如圖9-1，對(duì)折矩形紙片ABCD，使AD與BC重合，得到折痕EF，把紙片展平；再一次折疊紙片，使點(diǎn)A落在EF上的點(diǎn)N處，并使折痕經(jīng)過點(diǎn)B，得到折痕BM，把紙片展平，連接AN。折痕BM ? （填“是”或“不是”）線段AN的垂直平分線。

如圖9-2，繼續(xù)折疊紙片，使點(diǎn)A落在BC邊上的點(diǎn)H處，并使折痕經(jīng)過點(diǎn)B，得到折痕BG，把紙片展平，則∠GBN＝ ?? °。

如圖9-3，折疊矩形紙片ABCD，使點(diǎn)A落在BC邊上的點(diǎn)A'處，并且折痕交BC邊于點(diǎn)T，交AD邊于點(diǎn)S，把紙片展平，連接AA'交ST于點(diǎn)O，連接AT。求證：四邊形SATA′是菱形。

基礎(chǔ)性練習(xí)題來自課后習(xí)題，考查折痕的實(shí)質(zhì)以及正方形的判定；鞏固性練習(xí)題是學(xué)生日常生活中比較熟悉的折紙飛機(jī)，考查折疊前后兩個(gè)圖形全等的基本性質(zhì)；提高性練習(xí)題是在折60°角的基礎(chǔ)上設(shè)計(jì)的變式練習(xí)。這三道題與本節(jié)課內(nèi)容呼應(yīng)，可以考查學(xué)生對(duì)本節(jié)課內(nèi)容的掌握程度。

最后，筆者出示手折玫瑰花的圖片和折紙教程的二維碼，讓有興趣的學(xué)生課后參照視頻教程，嘗試折出一朵玫瑰花。

（作者單位：武漢市新洲區(qū)思源實(shí)驗(yàn)學(xué)校）

責(zé)任編輯? 孫愛蓉