漫談黃金分割

黃 雨 樊 濤

(安徽省淮南第二中學(xué))

0.618是一個(gè)令世界震驚的數(shù)字,在其中隱含著最美的比例,人體、雕塑、繪畫、圖形、建筑等,只要有優(yōu)美的外觀,必然蘊(yùn)含著這個(gè)數(shù)字,因此,人們將其稱為黃金分割比例(簡(jiǎn)稱黃金分割),它是數(shù)學(xué)大廈上一顆璀璨的明珠.

世人皆知,幾何學(xué)里有兩件瑰寶,一是勾股定理,二是黃金分割.有人說:“如果把勾股定理比作黃金礦的話,那么可以把黃金分割比作鉆石礦”,當(dāng)見黃金分割意義非凡.

一、黃金分割的由來

傳說兩千多年前,古希臘數(shù)學(xué)家畢達(dá)哥拉斯(Pythagoras,約公元前580年～約前500年)走在街上,當(dāng)路過一個(gè)鐵匠鋪時(shí)聽到“叮當(dāng)、叮當(dāng)……”的打鐵聲,一長(zhǎng)一短,非常悅耳,于是駐足傾聽.他發(fā)現(xiàn)聲音的節(jié)奏具有規(guī)律性,憑數(shù)學(xué)家的天賦,他把這種聲音的比例用數(shù)學(xué)的方式表達(dá)了出來.公元前4世紀(jì),古希臘數(shù)學(xué)家歐多克索斯系統(tǒng)地研究了這一問題,并建立起了比例理論.后來,數(shù)學(xué)家歐幾里得吸收了歐多克索斯的理論,并將其撰寫在《幾何原本》中,使得比例理論得到了進(jìn)一步的發(fā)展.我國(guó)著名數(shù)學(xué)家華羅庚推廣優(yōu)選法,其中最著名的就是0.618法,也稱黃金分割法.

1.1 黃金分割比的定義

如圖1,把一條線段分成兩段,如果較短的一段與較長(zhǎng)的一段的比等于較長(zhǎng)的一段與整條線段的比,那么這個(gè)比值就是黃金分割比.

圖1

1.2 黃金分割點(diǎn)的作法

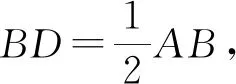
圖2(1)

②如圖2(2),以D為圓心,以BD為半徑作圓D,交AD于E點(diǎn);

③如圖2(3),以A為圓心,以AE為半徑作圓A,交AB于C點(diǎn),則C即為黃金分割點(diǎn).

1.3 黃金矩形的作法

①如圖3(1),在正方形ABCD中,取AB的中點(diǎn)E,連接EC;

圖3(1)

②如圖3(2),以E為圓心,以EC為半徑作圓E,交AB的延長(zhǎng)線于F點(diǎn);

③如圖3(3),以BC,BF為鄰邊構(gòu)造矩形BCGF,則矩形ADGF,BCGF都為黃金矩形.

二、黃金分割的發(fā)展

2.1 從斐波那契數(shù)列到黃金分割

意大利數(shù)學(xué)家列昂納多·斐波那契(Leonardo Fibonacci),生于公元1170年,卒于1250年,出生于比薩,他被人稱作“比薩的列昂納多”.他在建立養(yǎng)兔場(chǎng)的兔子演化模型時(shí)發(fā)現(xiàn)了數(shù)列{Fn}:1,1,2,3,5,8,13,21,34,55,89,144,….滿足從第三項(xiàng)起,每一項(xiàng)都是前兩項(xiàng)之和,即:Fn+2=Fn+1+Fn(n∈N*),此數(shù)列稱為斐波那契數(shù)列,戲稱兔子數(shù)列.

(1)數(shù)字特征

數(shù)列相除小數(shù)數(shù)列相除小數(shù)數(shù)列相除小數(shù)F2=1F1F21F8=21F7F80.619 047 619F14=377F13F140.618 037 135F3=2F2F30.5F9=34F8F90.617 647 059F15=610F14F150.618 032 787F4=3F3F40.666 666 667F10=55F9F100.618 181 818F16=987F15F160.618 034 448F5=5F4F50.6F11=89F10F110.617 977 528F17=1597F16F170.618 033 813F6=8F5F60.625F12=144F11F120.618 055 556F18=2584F17F180.618 034 056F7=13F6F70.615 384 615F13=233F12F130.618 025 751F19=4181F18F190.618 033 963

(2)理論證明

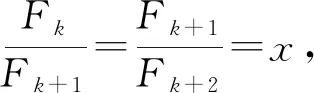
方法二:Fn+2=Fn+1+Fn,根據(jù)遞推數(shù)列的解法,建立方程,利用根來構(gòu)造數(shù)列.

2.2 從斐波那契螺旋線到黃金分割比例構(gòu)圖

生活中我們能夠觀察到芭蕾舞演員會(huì)踮起腳尖舞蹈,女生喜歡穿高跟鞋,著名雕像被故意延長(zhǎng)了雙腿,攝影師構(gòu)圖會(huì)把主體物放在旋渦中心.這些舉動(dòng)是否有科學(xué)依據(jù),筆者帶著疑問來研究斐波那契螺旋線.

(1)圖形特征

分別以斐波那契數(shù)為邊長(zhǎng)作正方形,然后將它們拼成矩形,在每個(gè)正方形中畫一個(gè)90°的扇形,連起來的弧線就是斐波那契螺旋線,又稱黃金螺旋線,拼成的矩形近似為黃金矩形.如下圖4(1)所示.

圖4(2)

圖4(3)

(2)黃金構(gòu)圖

攝影師會(huì)把主體物放到旋渦中心點(diǎn)(圖4(2)),讓其他的輔助畫面圍繞黃金螺旋線.世界名畫《蒙娜麗莎的微笑》(圖4(3))也是用黃金分割比例構(gòu)圖的.從它們身上發(fā)現(xiàn),優(yōu)美的構(gòu)圖其實(shí)就是在整體和局部反復(fù)地使用黃金分割.黃金分割具有比例性、藝術(shù)性、和諧性,蘊(yùn)含著豐富的美學(xué)價(jià)值,即是美的密碼.

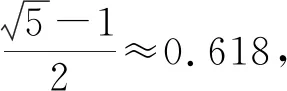
三、試題中的黃金分割

3.1 高考試題

( )

A.165 cm B.175 cm

C.185 cm D.190 cm

【分析】根據(jù)黃金分割比,作出頭頂、咽喉、肚臍、足底的簡(jiǎn)圖.

圖5(1)

圖5(2)

圖5(3)

【點(diǎn)評(píng)】本題以最美人體為背景,考查了黃金分割、估算以及不等式等必備知識(shí),考查了邏輯思維能力、運(yùn)算求解能力、創(chuàng)新能力等關(guān)鍵能力,引導(dǎo)教學(xué)注重培養(yǎng)數(shù)學(xué)運(yùn)算和邏輯推理核心素養(yǎng).難點(diǎn)在于從兩個(gè)不同的角度進(jìn)行估算運(yùn)算,考查創(chuàng)新能力.

【變式1】(背景同上題)某女生頭頂至咽喉的長(zhǎng)度為25 cm,肚臍至足底的長(zhǎng)度為103 cm,肚臍以上滿足黃金分割比例,則該女生應(yīng)選擇多高的鞋子,才能最接近滿足上述兩個(gè)黃金分割比例

( )

A.2 cm B.3 cm

C.4 cm D.5 cm

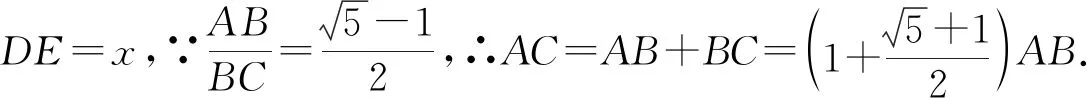
【點(diǎn)評(píng)】高跟鞋的選擇是有科學(xué)依據(jù)的,并不是越高越好,要從審美的角度進(jìn)行分析.

( )

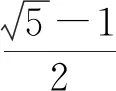
圖6

A.29 m B.29.8 m

C.30.8 m D.32.8 m

【分析】由矩形ABCD和EBCF是黃金矩形,由邊長(zhǎng)的比求出AB范圍.

【點(diǎn)評(píng)】本題以黃金矩形為背景,考查黃金分割、估算、不等式等必備知識(shí),考查了邏輯思維能力、運(yùn)算求解能力、創(chuàng)新能力等關(guān)鍵能力,引導(dǎo)教學(xué)注重培養(yǎng)數(shù)學(xué)運(yùn)算和邏輯推理核心素養(yǎng).難點(diǎn)在于從兩個(gè)不同的角度進(jìn)行估算運(yùn)算,考查創(chuàng)新能力.

( )

圖7

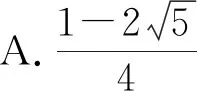
故選C.

【點(diǎn)評(píng)】本題以黃金三角形為背景,考查利用二倍角公式以及誘導(dǎo)公式求值等必備知識(shí),考查了邏輯思維能力、運(yùn)算求解能力等關(guān)鍵能力,引導(dǎo)教學(xué)注重培養(yǎng)數(shù)學(xué)運(yùn)算和邏輯推理核心素養(yǎng).

3.2 命題導(dǎo)向

以實(shí)際問題為背景,考查必備的基礎(chǔ)知識(shí),強(qiáng)調(diào)知識(shí)之間的內(nèi)在聯(lián)系,引導(dǎo)學(xué)生建立完備的數(shù)學(xué)知識(shí)體系.考查邏輯思維能力、運(yùn)算求解能力、創(chuàng)新能力等關(guān)鍵能力,引導(dǎo)教學(xué)注重培養(yǎng)核心素養(yǎng)和數(shù)學(xué)能力.