基于邏輯主線、課程主題的數(shù)學(xué)整體性教學(xué)的實(shí)踐與思考
——關(guān)于“手電筒模型”解題教學(xué)問題診斷與分析解決的案例實(shí)錄

陳偉流

(廣東省惠州市仲愷中學(xué))

一、教學(xué)前言

《普通高中數(shù)學(xué)課程標(biāo)準(zhǔn)(2017年版)》在教學(xué)實(shí)施中強(qiáng)調(diào):教師要進(jìn)一步精選學(xué)科內(nèi)容,重視以主題為引領(lǐng),使課程內(nèi)容結(jié)構(gòu)化,促進(jìn)學(xué)科素養(yǎng)的落實(shí),隨后的2020年修訂版課標(biāo)又強(qiáng)調(diào):關(guān)注同一主線內(nèi)容的邏輯關(guān)系,關(guān)注不同數(shù)學(xué)知識(shí)蘊(yùn)含的通性通法、數(shù)學(xué)思想.數(shù)學(xué)內(nèi)容的展開應(yīng)循序漸進(jìn)、螺旋上升,并使之成為一個(gè)有機(jī)的整體.

具體到解析幾何模塊的解題教學(xué)實(shí)踐,不少教師因試題的綜合性強(qiáng)、推理量大、變化情境雜而停留于就題論題、點(diǎn)到為止、輕視知識(shí)關(guān)聯(lián)性等特征的淺層教學(xué)階段中,使得學(xué)生出現(xiàn)思維混亂、認(rèn)知偏差等帶有負(fù)遷移的不良心理因素,以至于無法充分挖掘試題的隱含條件,無法調(diào)動(dòng)對(duì)已學(xué)知識(shí)的靈活運(yùn)用,更難以凝練出具有知識(shí)統(tǒng)攝性的數(shù)學(xué)模型.基于新課標(biāo)的指導(dǎo)理念及上述教與學(xué)的現(xiàn)狀,筆者以邏輯主線及課程主題為統(tǒng)領(lǐng)思想進(jìn)行數(shù)學(xué)整體性教學(xué),以解析幾何中“手電筒模型”解題教學(xué)問題診斷與分析解決的案例為切入點(diǎn),淺談在創(chuàng)設(shè)情境,初探模型;多變情景,深化模型;變式應(yīng)用,完善認(rèn)知等多個(gè)教學(xué)環(huán)節(jié)中的些許設(shè)計(jì)心得.

二、教學(xué)目標(biāo)解析

(1)理解動(dòng)直線具備定斜率和過定點(diǎn)等屬性的根源,培養(yǎng)發(fā)現(xiàn)問題的基本能力;

(2)理解“引雙直線的定點(diǎn)” “斜率和(積)為定值” “定斜率或過定點(diǎn)”三要素的整體封閉性,提升分析問題的能力,滲透模型思想,提升數(shù)學(xué)抽象、邏輯推理、數(shù)學(xué)建模等核心素養(yǎng).

經(jīng)過本次課堂學(xué)習(xí),學(xué)生能初步形成“手電筒模型”的數(shù)學(xué)模型基本知識(shí)理論體系,在積累多維的數(shù)學(xué)活動(dòng)經(jīng)驗(yàn)后,明確定值、定點(diǎn)等知識(shí)的邏輯關(guān)系,在變式訓(xùn)練中積累逆向活動(dòng)經(jīng)驗(yàn),從而理解數(shù)學(xué)知識(shí)的內(nèi)在邏輯,培養(yǎng)數(shù)學(xué)探索、數(shù)學(xué)應(yīng)用的理性思維,體會(huì)所學(xué)知識(shí)創(chuàng)造性解決問題的成就感,實(shí)現(xiàn)數(shù)學(xué)知識(shí)的育人價(jià)值.

三、教學(xué)問題診斷分析

(1)學(xué)生已基本熟知解析幾何模塊的基礎(chǔ)知識(shí)、基礎(chǔ)思想及基礎(chǔ)應(yīng)用,有一定的推理運(yùn)算素養(yǎng).課堂中教師需引導(dǎo)學(xué)生以邏輯主線的視角審視斜率和(積)與定斜率、定點(diǎn)問題,能夠主動(dòng)發(fā)現(xiàn)問題間的脈絡(luò)關(guān)系并在腦海中形成相關(guān)模型體系,繼而凝練出課程主題——“手電筒模型”.

(2)在教學(xué)環(huán)節(jié)的逐步推進(jìn)中,學(xué)生積累由易到難、由淺到深、由特殊到一般的活動(dòng)經(jīng)驗(yàn),能初步形成“手電筒模型”的雛形,認(rèn)識(shí)動(dòng)直線具備定斜率或過定點(diǎn)的條件,但對(duì)于三要素間的統(tǒng)一封閉性較為陌生,需教師在變式中深化學(xué)生對(duì)三要素的認(rèn)知,讓學(xué)生體會(huì)豁然開朗的頓悟感,促進(jìn)知識(shí)、技能的全面內(nèi)化,避免教與學(xué)出現(xiàn)“兩張皮”的脫離現(xiàn)象.基于上述分析,明確本設(shè)計(jì)的重點(diǎn)為理解“手電筒模型”中關(guān)聯(lián)定值、定點(diǎn)問題的知識(shí)邏輯體系.難點(diǎn)是理解“手電筒模型”中三要素的邏輯關(guān)系.

四、教學(xué)過程設(shè)計(jì)

環(huán)節(jié)一 創(chuàng)設(shè)情境,初探模型

【問題1】經(jīng)歷設(shè)點(diǎn),設(shè)線,曲直聯(lián)立,韋達(dá)定理介入等步驟,可計(jì)算得出動(dòng)直線PQ有定斜率-1(過程略).在此基礎(chǔ)上,同學(xué)們能否順便計(jì)算出雙曲線在點(diǎn)A處的切線斜率?(A處的切線斜率k1為1)

【追問1】在本例中l(wèi)PQ的斜率與A處切線斜率k1互為相反數(shù),這是偶然還是必然?

在現(xiàn)代信息技術(shù)GeoGebra的平臺(tái)中,教師還原本例的所有幾何要素,如圖1,拖動(dòng)點(diǎn)A,保持直線AP,AQ斜率之和為0,從直觀角度可驗(yàn)證lPQ與雙曲線在動(dòng)點(diǎn)A處的切線斜率k1始終互為相反數(shù).

圖1

【評(píng)注】以雙曲線為背景,由引兩直線的定點(diǎn),斜率和為0推導(dǎo)出動(dòng)直線有定斜率的規(guī)律屬性,為進(jìn)一步推廣到圓錐曲線體系做好鋪墊.

【追問2】若將問題背景切換為橢圓、拋物線或圓,其他條件不變,問動(dòng)直線是否仍有定斜率?在GeoGebra的平臺(tái)中依次在曲線上取定點(diǎn)A,過A作斜率互為相反數(shù)的兩直線交曲線于P,Q兩點(diǎn),觀察動(dòng)直線PQ斜率與A處切線斜率k1,有何發(fā)現(xiàn)(如圖2,3,4)?針對(duì)上述數(shù)學(xué)實(shí)驗(yàn)?zāi)芊窠o出統(tǒng)一的定性結(jié)論?

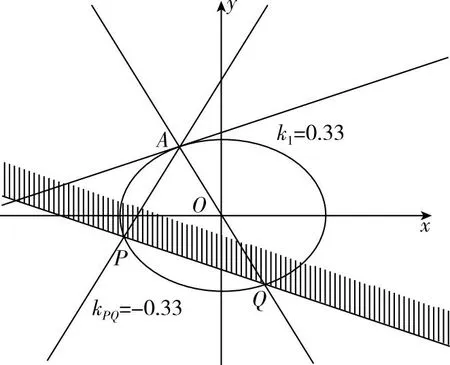
圖2

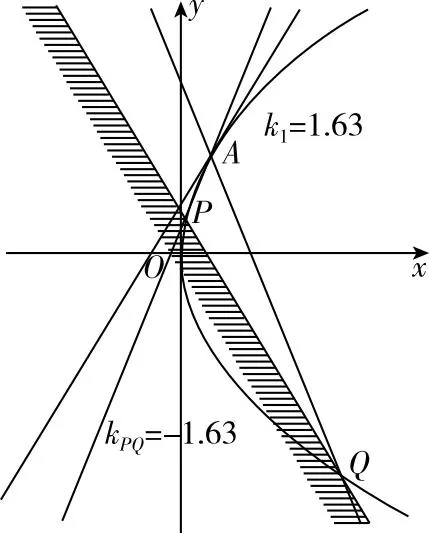
圖3

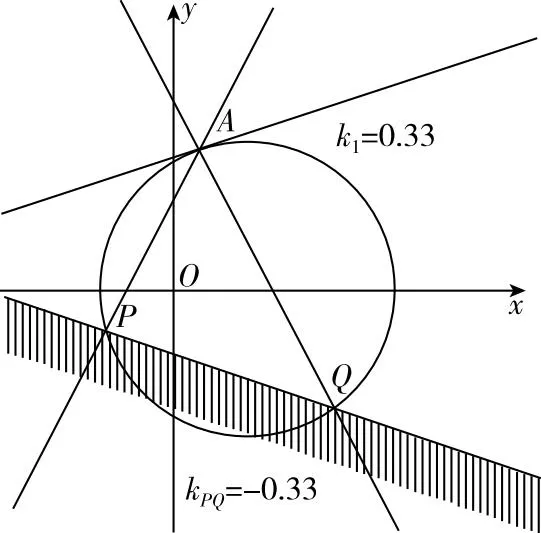
圖4

【結(jié)論1】在圓錐曲線上取定點(diǎn)A(x0,y0)(y0≠0),過A作斜率為相反數(shù)的兩直線交曲線于P,Q兩點(diǎn),圓錐曲線在點(diǎn)A處的切線斜率為k1,若

點(diǎn)A在橢圓x2a2+y2b2=1(a>b>0)上,點(diǎn)A在雙曲線x2a2-y2b2=1(a,b>0)上,點(diǎn)A在拋物線y2=2px(p>0)上,點(diǎn)A在圓x2+y2+Dx+Ey+F=0(D2+E2-4F>0)上,則kPQ=b2x0a2y0=-k1則kPQ=-b2x0a2y0=-k1則kPQ=-py0=-k1則kPQ=x0+D2y0+E2=-k1

【評(píng)注】通過問題情境的探究活動(dòng),揭示定點(diǎn)、斜率和為0、定斜率三要素在圓錐曲線體系間存在普遍性、統(tǒng)一性的內(nèi)在規(guī)律,水到渠成般地形成命題和結(jié)論,感悟問題的通法通性.圖象的動(dòng)態(tài)可視化反映了變化中的不變性與規(guī)律性,以及對(duì)稱性,體現(xiàn)變化中的對(duì)稱美與和諧美,有利于激發(fā)學(xué)生的理性探索精神,反映數(shù)學(xué)美學(xué)的育人價(jià)值.

環(huán)節(jié)二 多變情景,深化模型

【問題2】如果改變例1中斜率和為0的條件,動(dòng)直線PQ仍有定斜率嗎?動(dòng)直線PQ是否有如過定點(diǎn)等其他屬性?

【追問3】承接例1的解題經(jīng)驗(yàn),其求解過程在例2中是否具有普適性與通用性?

【評(píng)注】引導(dǎo)學(xué)生在解題實(shí)踐中,認(rèn)識(shí)到解法上的共性特征,凝練出通法思維.增設(shè)傾斜角和為定值的變式情境,旨在引導(dǎo)學(xué)生如何有效解讀條件,合理建立陌生條件與所學(xué)知識(shí)的溝通橋梁,化陌生為熟悉.

【追問4】由此可知,在雙曲線背景中,當(dāng)斜率和積為非零定值時(shí),動(dòng)直線PQ有過定點(diǎn)屬性;若將斜率和(積)為非零定值的條件推廣到橢圓、拋物線中時(shí),其定點(diǎn)屬性是否仍成立?

【評(píng)注】以變式教學(xué)為切入手段,以斜率和(積)為定值為課堂統(tǒng)領(lǐng)主線串聯(lián)起定斜率和過定點(diǎn)的兩個(gè)問題,保證了學(xué)生知識(shí)學(xué)習(xí)中的邏輯關(guān)聯(lián)性和認(rèn)識(shí)結(jié)構(gòu)上的自然過渡性,為進(jìn)一步開展“手電筒模型”的主題凝練做好鋪墊.

圖5

圖6

圖7

圖8

圖9

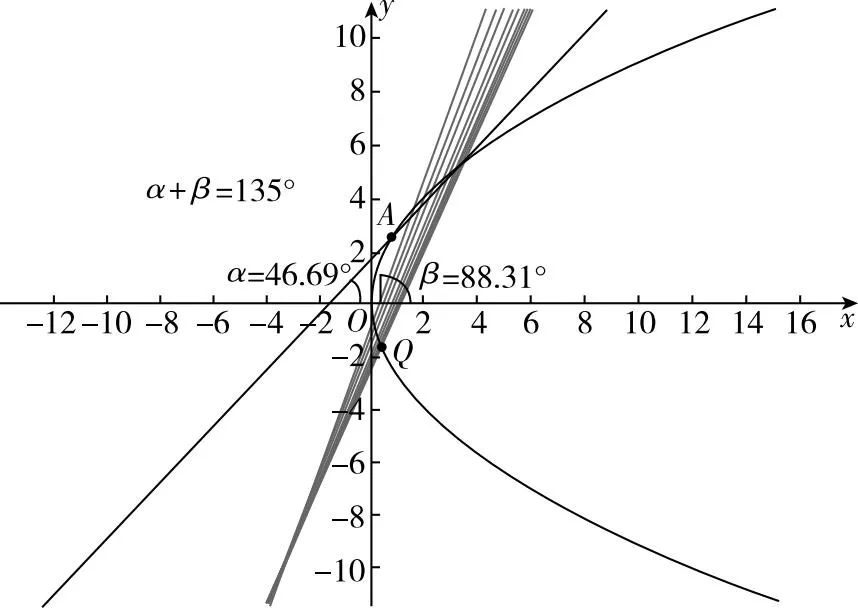
圖10

【追問5】通過可視化動(dòng)態(tài)分析,是否能得出對(duì)斜率和(積)為非零定值與直線過定點(diǎn)的邏輯關(guān)系作出統(tǒng)一定性表述?

【結(jié)論2】在圓錐曲線上取定點(diǎn)A(x0,y0)(y0≠0),過A作斜率存在的兩直線交曲線于P,Q兩點(diǎn),若兩直線

斜率和為λ(λ≠0)斜率積為λ(λ≠0)兩直線傾斜角滿足tan(α+β)=λ(λ≠0)橢圓lPQ過定點(diǎn)x0-2y0λ,-y0-2b2x0λa2 λ=b2a2,kPQ=-y0x0(x0≠0)λ≠b2a2,lPQ過定點(diǎn)λa2+b2λa2-b2x0,-b2-λa2λa2-b2y0 lPQ過定點(diǎn)-2a2y0-(b2+a2)λx0λ(a2-b2) ,2b2x0-(b2+a2)λy0λ(a2-b2) 雙曲線lPQ過定點(diǎn)x0-2y0λ,-y0+2b2x0λa2 λ=-b2a2,kPQ=-y0x0(x0≠0)λ≠-b2a2,lPQ過定點(diǎn)λa2-b2λa2+b2x0,b2-λa2λa2+b2y0 lPQ過定點(diǎn)-2a2y0+(b2-a2)λx0λ(a2+b2) ,2b2x0+(b2-a2)λy0λ(a2+b2) 拋物線lPQ過定點(diǎn)x0-2y0λ,-y0+2pλ lPQ過定點(diǎn)x0-2pλ,-y0 lPQ過定點(diǎn)x0-2p-2pλ,-y0+2pλ

【評(píng)注】在多層次的探究變式的情境中培養(yǎng)學(xué)生在解題實(shí)踐中養(yǎng)成思考并解決問題的習(xí)慣,以通法貫穿問題的運(yùn)算推理過程,將新通性規(guī)律通過技術(shù)引領(lǐng),從形象到抽象總結(jié)為更一般的結(jié)論并用數(shù)學(xué)語(yǔ)言表示,教師帶領(lǐng)學(xué)生經(jīng)歷從特殊到一般,從感性到理性,從定性到定量的研究過程,升華思維的同時(shí)提升了邏輯推理、數(shù)學(xué)抽象等素養(yǎng).

環(huán)節(jié)三 變式應(yīng)用,完善認(rèn)知

【問題3】在上述探索中,若改變“曲線上的定點(diǎn)” “斜率和或積為定值” “動(dòng)直線有定斜率或過定點(diǎn)”這三要素的邏輯結(jié)構(gòu),是否依然滿足知二求一的封閉性?

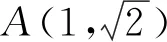
(1)求橢圓C的方程;

(2)求證:直線AB,AD的斜率之和為定值.

例4(2021·河南洛陽(yáng)一模)設(shè)拋物線C:y2=2px(p>0)的焦點(diǎn)為F,點(diǎn)P(4,m)(m>0)是拋物線上一點(diǎn)且|PF|=5.

(1)求拋物線的方程;

(2)過點(diǎn)Q(1,-4)的直線與拋物線交于A,B兩點(diǎn)(均與點(diǎn)P不重合).設(shè)直線PA,PB的斜率分別為k1,k2,求證:k1·k2為定值.

【評(píng)注】學(xué)生在前文的探索環(huán)節(jié)中對(duì)三要素邏輯關(guān)系打下一定的認(rèn)知基礎(chǔ),該環(huán)節(jié)以變式訓(xùn)練切入,旨在打破其認(rèn)知刻板印象,豐富并完善其對(duì)三要素的認(rèn)識(shí)結(jié)構(gòu)層次,為引導(dǎo)學(xué)生基于知識(shí)整體上提煉模型主題積累充分的認(rèn)知活動(dòng)經(jīng)驗(yàn).

本課堂的教學(xué)環(huán)節(jié)以斜率和(積)作為切入條件拉開序幕,到斜率和(積)為定值作結(jié)論收尾,課堂中的諸多設(shè)計(jì)永遠(yuǎn)圍繞著邏輯主線——“斜率和(積)與定斜率定點(diǎn)問題”來展開,循序漸進(jìn)般拾級(jí)而上,在知識(shí)體系上有效整合了眾多教學(xué)內(nèi)容,使各個(gè)教學(xué)要素成為有邏輯關(guān)聯(lián),有通性規(guī)律,有模型思想的數(shù)學(xué)結(jié)構(gòu),此時(shí),基于學(xué)生認(rèn)知結(jié)構(gòu)的建立過程,“手電筒模型”的主題便可水到渠成般自然凝練而成!

“手電筒模型”:在平面直角坐標(biāo)系中,已知?jiǎng)又本€與圓錐曲線交于兩動(dòng)點(diǎn),從圓錐曲線上的一定點(diǎn)向兩動(dòng)點(diǎn)引兩直線,則兩直線的斜率和(積)為定值的充要條件是兩點(diǎn)所在的動(dòng)直線具有定向(定斜率)或過定點(diǎn)的不變屬性,因其幾何圖形的形象特征可稱其為“手電筒模型”.

五、展望思考

1.把握“邏輯主線”,服務(wù)“深度備課”

《高考評(píng)價(jià)體系》在四翼的綜合性考查中強(qiáng)調(diào):要求學(xué)生對(duì)同一層面的知識(shí)、能力、素養(yǎng)能夠橫向整合貫通,形成完整的知識(shí)結(jié)構(gòu)、能力結(jié)構(gòu)網(wǎng)絡(luò);對(duì)不同層面的知識(shí)、能力、素養(yǎng)能夠縱向融會(huì)貫通.由此可見,在解題教學(xué)實(shí)踐中,教師要基于知識(shí)發(fā)展,學(xué)生學(xué)情等實(shí)際情況,以知識(shí)關(guān)聯(lián)為邏輯主線進(jìn)行課堂的整體設(shè)計(jì),將教學(xué)內(nèi)容循序漸進(jìn),螺旋上升,以點(diǎn)帶面般展開,使之構(gòu)成一個(gè)可延伸、耐推敲、有活力的有機(jī)整體,最終實(shí)現(xiàn)教師的深度備課.如本案例中,課堂多個(gè)環(huán)節(jié)的實(shí)施始終圍繞著斜率和(積)與定向定點(diǎn)問題為核心主線統(tǒng)攬全局,并將教學(xué)內(nèi)容的安排每一步都放到課堂活動(dòng)的大系統(tǒng)中考量,主次分明,目標(biāo)清晰,結(jié)構(gòu)緊湊,緊密相連,合乎邏輯,而并非一味地追求教學(xué)內(nèi)容的深度、難度及廣度,或是片面地突出或強(qiáng)調(diào)某一點(diǎn).

2.問題引領(lǐng),推進(jìn)活動(dòng),凝練主題

因?qū)W生思維視野、知識(shí)水平及能力素養(yǎng)方面存在不同程度、不同方面的欠缺,本案例中試題的求解分析及結(jié)論的歸納總結(jié)等過程必然使部分學(xué)生倍感吃力而心生畏難情緒,所以筆者根據(jù)知識(shí)、學(xué)情、技術(shù)等客觀因素在深度備課中進(jìn)行多維預(yù)設(shè),圍繞內(nèi)容主線設(shè)置符合學(xué)生認(rèn)知規(guī)律的啟發(fā)性問題,進(jìn)而展開定斜率幾何意義的探索、GeoGebra技術(shù)的直觀探路、特殊到一般的歸納總結(jié)、變式教學(xué)的鋪墊過渡、條件結(jié)論互逆的解題體驗(yàn)等多維學(xué)習(xí)活動(dòng),一步步逐級(jí)推進(jìn),使得“手電筒模型”的主題生成得以順利開展,學(xué)生知其然,更知其所以然,如此才能帶動(dòng)學(xué)生的思維品質(zhì)、學(xué)習(xí)能力不斷地拾級(jí)而上.

3.關(guān)注能力成長(zhǎng),提升學(xué)習(xí)品質(zhì)

章建躍博士曾指出:教學(xué)設(shè)計(jì)應(yīng)充分體現(xiàn)數(shù)學(xué)的整體性、邏輯的連貫性、思想的一致性、方法的普適性、思維的系統(tǒng)性,切實(shí)防止碎片化教學(xué),通過有效的四基、四能教學(xué),使數(shù)學(xué)學(xué)科核心素養(yǎng)真正落實(shí)于數(shù)學(xué)課堂,基于此,本案例以邏輯主線及課程主題為導(dǎo)向進(jìn)行數(shù)學(xué)整體性設(shè)計(jì),學(xué)生擺脫了淺層教學(xué)中僅掌握知識(shí)技能、思想方法等低階要求,實(shí)現(xiàn)了數(shù)學(xué)思維、數(shù)學(xué)語(yǔ)言、實(shí)踐能力、批判精神、創(chuàng)新能力等學(xué)習(xí)品質(zhì)方面的發(fā)展和精進(jìn),最終到達(dá)整體性教學(xué)所指向的彼岸遠(yuǎn)方——深度學(xué)習(xí).回顧課堂各個(gè)環(huán)節(jié),教師通過問題的精心設(shè)計(jì)和可視化輔助軟件的巧妙安排,無不是為了讓學(xué)生立足四基以發(fā)展四能,能在探尋不變性及規(guī)律性的過程中,激發(fā)數(shù)學(xué)學(xué)習(xí)的興趣,培養(yǎng)良好的學(xué)習(xí)習(xí)慣,提升數(shù)學(xué)應(yīng)用意識(shí),審美價(jià)值等理性思維,最終促進(jìn)學(xué)生學(xué)會(huì)深度學(xué)習(xí),以期提升數(shù)學(xué)素養(yǎng),引導(dǎo)學(xué)生在將來的學(xué)習(xí)中,會(huì)用數(shù)學(xué)眼光觀察世界,會(huì)用數(shù)學(xué)思維思考世界,會(huì)用數(shù)學(xué)語(yǔ)言表達(dá)世界.