自適應分塊的改進最小費用網絡流解纏算法

張金翼，王 輝，吳思利，鄭世超，顧約翰

（1.上海衛星工程研究所，上海 201109；2.上海市毫米波空天信息獲取及應用技術重點實驗室，上海 201109）

0 引言

近年來，地下資源的過度開采、水土流失等問題愈發嚴重，地質災害（如地震、泥石流、礦區塌陷、城市地面沉降）頻發，對我國人民群眾的生命及財產安全造成威脅。在該類災害中典型的表征為地表形變，因此監測地表形變是防災減災的重要手段。傳統的測量地表形變技術手段為水準測量、GPS 測量等［1］，但上述方法存在費時、費力、數據點孤立的缺陷，無法及時、高效地預測和評估地質災害。差分干涉合成孔徑雷達（Differential Interferometric Synthetic Aperture Radar，DInSAR）是天基遙感中較為常用的測量地表形變的技術手段，因為全天時、全天候工作，速度快、范圍廣、測量密度高等特點逐漸受到人們的重視［2-3］，差分干涉合成孔徑雷達形變測量主要利用相位的變化，直接測得的干涉相位被包裹在［-Π，Π）)[-π，π 內，要獲得可用的相位信號須對其進行解纏繞，其效果對測量的精度有較大的影響［4-5］。

常用的解纏方法按照原理分為以下3 類：1）基于路徑跟蹤解纏，選擇不同的路徑對相鄰像元進行差值積分恢復真實相位，較有代表性的是GOLSTEIN［6］于1988 年提出的枝切法，可在計算出殘差點后，快速有效地尋找連接相鄰殘差點的最優路徑；2）基于最小范數思想，通過擬合函數求得纏繞相位和解纏相位的離散偏微分差，進而求解相位解纏的整體最佳估計值，其中較為常用的是最小二乘法、Jacobi 迭代法、Gauss-Seidel 迭代法和逐次超松弛（Successive Over Relaxation，SOR）迭代法，這些算法的缺陷在于數據量較大時收斂速度慢，不適用于大規模數據［7-8］；3）基于網絡規劃的算法，由COSTANTINI［9］于1996 年提出，網絡規劃算法 在相位解纏中引入最小代價流的概念，通過搜索全區域最短路徑生成最優枝切線進行解纏，可以將誤差限制在相干質量差的區域內，保證其余區域結果的準確性，精度較高，因此常被用作其他算法的精度參照，但由于最小費用網絡流（Minimum Cost Network Flow，MCF）的算法特性，當相位差圖像相干性差、殘差點數量多時，算法的復雜度較高，效率較低［10-12］。CHEN［13］提出改進的MCF 算法，分割整個圖像，與傳統的MCF 算法相比，提高了算法效率，但分塊的規模為人工設定，沒有具體的標準，不同的分塊大小會對該算法的精度產生較大影響。

本文提出一種基于自適應分塊的改進MCF 解纏算法，該方法根據質量圖所表現的殘差信息，將分塊大小進行自適應尋優，更多地將高相干區域劃分在一個子塊。實驗結果表明，該算法在提升算法效率的同時保證了準確度，有效地拓展了MCF 算法的應用場景。

1 MCF 算法解纏原理

相位解纏的基本思路是將已獲取的干涉圖中的纏繞相位，通過疊加纏繞數恢復相位的真實值，進而反映真實的形變情況［14-15］。

定義纏繞相位為ψi，j，真實相位為?i，j，對于一個M×N的矩陣，可得方程式如下：

式中：k為整數，0 ≤i≤M-1，0 ≤J≤N-1。

定義纏繞算子W，對相鄰像素間的纏繞相位進行±2kπ 的操作，使其變為真實相位。定義x方向和y方向上的絕對相位差分別為，其方程式如下：

式中：ψi+1，j為M×N矩陣中(i+1，j)處點的纏繞相位，rad；ψi，j+1為M×N矩陣中(i，j+1)處點的纏繞相位，rad。

由式（2）變換可得方程式如下：

對于干涉圖中大部分點，沿著點(i，j)、(i+1，j)、(i+1，j+1)、(i，j+1)的纏繞相位差環路積分為0，而實際應用中，由于噪聲等因素的存在導致出現殘差點，殘差點處的纏繞相位差環路積分為±2π，即定義殘差為

式 中：ei，j為殘差；為(i+1，j)點在y方向上的絕對相位差，單位為rad；為(i，j+1)點 在x方向上的絕對相位差，單位為rad。

由于存在殘差點，無法確定干涉圖全圖的積分，其變成與積分路徑有關的變量，因此需考慮殘差點的影響，使其降至最小。在最小費用流解纏算法中，將正/負殘差點定義為供應/需求節點，殘差為供應/需求量，將其他點定義為轉運節點。相鄰的節點之間通過帶有流的弧連接，以調節供需平衡，最小費用流解纏的目的是在所有節點供需平衡的基礎上，確保總費用取最小。達到供需平衡即［16-18］：

式 中：為 點(i，j)到點(i+1，j)的流量；為點(i，j)到點(i，j+1)的流量，1 ≤i≤M-1，1 ≤j≤N-1。

總費用流為

式中：為點(i，j)到點(i+1，j)對應的費用；為點(i，j)到點(i，j+1)的費用。

式中：ψ0，0為（0，0）位置處點的纏繞相位，rad。

綜上所述，應用MCF 算法的解纏步驟如下。

1）對相干圖做預處理，選定閾值，提取相干系數高于閾值的相位。

2）在相位的集合中建立Delaunay 三角網，進而構建對偶圖，將殘差映射到對偶網絡中。

3）在對偶網絡中，應用最小費用流法連接正負殘差點對，計算最小費用流集合。

4）根據流的大小和方向對相位矩陣積分，得到解纏結果，再從高質量區域向低質量區域積分［12］。

2 自適應分塊的改進MCF 解纏算法

MCF 算法一經推出，其準確度便得到肯定，但隨著殘差點的增多，該算法的效率有所下降，因此提高算法效率是優化該算法的一個方向［16］。CHEN［13］提出改進的MCF 算法，將整個相干圖劃分為不重疊的矩形塊，將矩形塊作為完全獨立的圖像進行相位解纏，降低解纏過程中所需的內存資源，提高效率。

原始相干圖使用MCF 算法解纏的算法復雜度可表示為O(N2)，其中N為圖中殘點的數量，將相干圖分為i個矩形塊，則分割后算法復雜度可表示為O(N12+N22+N32+…+Ni2)，其 中N1+N2+N3+…+Ni=N，后者的算法復雜度遠小于前者。

該種方法雖然提升了相位解纏的效率，但由于分割大小的不同會導致解纏精度的不穩定。在本文中引入一種基于質量圖的自適應分塊改進MCF算法，切割時，根據質量圖自適應選取分割大小，保留相干性較強的區域，在提高效率的同時保證精度。

本文提出的算法流程如下。

1）對相干圖做預處理，選定閾值，提取相干系數高于閾值的相位。

2）根據相干系數的計算方式計算質量圖。

在干涉SAR 中殘差點的存在是由于SAR 疊掩或去相關噪聲引起的，因此相關系數較低的區域其殘差點較多，相關系數較高的區域殘差點較少。一般將表征干涉圖像各點相位的特征圖稱為質量圖，質量圖可劃分為相干系數圖、偽相干系數圖、相位導數變化圖及最大相位梯度圖4 種，本文采用使用范圍較廣的相干系數圖［20］。

相干系數圖中各個區域之間的相干性通過相干系數表示，相干系數值較高表示2 個區域之間的相關性較好，即相位信息準確；相干系數值較低說明2 個區域之間相關性較差，即相位信息有誤。A、B2 張復圖像的相干系數可表示為

式中：E為求期望；γ為相干系數；B*為B的共軛。

3）根據質量圖選定應進行分割的塊的尺寸。

質量圖表示相干系數的大小，在最小費用流解纏方法中，影響解纏效率與準確度的是干涉圖中集中存在的殘差點。因此在分割時，將相干性較強的區域集中在一起，進而使得殘差點被零散的分割到各個子塊內，提高每個分割塊的解纏效率。

在實際操作過程中，為濾去噪聲求整張質量圖的均值，將其作為門限濾波，表達式為

式中：T為門限值；M、N為質量圖規模；f(i，j)為(i，j)位置點的相干系數。

在選擇分塊尺寸的過程中，選用密度峰值聚類算法。該算法是目前較為先進的聚類算法，需要較少的輸入參數，能檢測聚類中心，具有簡單、聚類速度快、穩定性好、聚類高效的優點，且對噪聲不敏感，是較為理想的聚類算法［21-22］。

對于質量圖中的數據，采用歐氏距離計算兩點之間的相似性：

式中：(xi，xj)為第i個點和第j個點；l為維度；m為維度的數量。

計算數據集中每個數據點的密度，表達式如下：

式中：S(m)為判斷函數；dc為截斷距離，設定為5。

當m≥0 時S(m)=1；當m≤0 時S(m)=0。

依照式（11），即可計算得到以每一點為中心的與其距離小于5 的點的個數，再求取每一數據點與其他密度比其大的數據點間的最小距離，如該點密度最大，則取與其他數據點距離的最大值為

式中：di，j為第i個點與第j個點的距離。

求得密度及最小距離后，將橫軸表示數據點的密度，縱軸表示數據點的最小距離，選取密度高且距離大的點作為聚類中心點，再將其他點按密度值降序排列，歸于聚類中心點［23-25］。

得到聚類結果后，將聚類點所在的矩形區域作為參考的干涉圖分塊區域，如聚類后產生多個子塊，將其大小取均值作為最終的分塊參考大小。

依照此方法得到的分塊可將相干性較強的點集中在同一塊區域，并依照大小劃分其他區域，提高算法的效率和準確度。

4）在相位的集合中建立Delaunay 三角網，進而構建對偶圖，將殘差映射到對偶網絡中。

5）在對偶網絡中應用最小費用流法連接正負殘差點對，計算最小費用流集合。

6）根據流的大小和方向對相位矩陣積分，得到解纏結果，再從高質量區域向低質量區域積分［12］。

算法流程如圖1 所示。

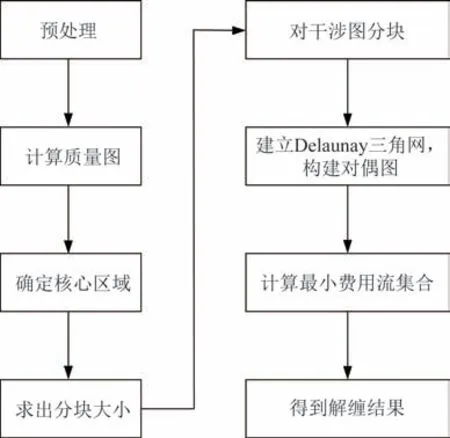
圖1 自適應分塊的改進MCF 解纏算法流程Fig.1 Flow chart of the improved MCF unwrapping algorithm with adaptive chunking

3 仿真實驗及結果分析計算機模擬結果

仿真實驗在一臺配備Intel Core i7-10750H 處理器（2.6 GHz，6 核12 線程）、NVIDIA GeForce GTX 1660 Ti GPU（6 GB 顯存）和16 GB DDR4 內存的計算機上進行，運行于Windows 10 操作系統，使用Matlab R2019b 仿真，在該平臺生成干涉條紋圖，并按照本文方法對其解纏繞，解纏前干涉如圖2所示。

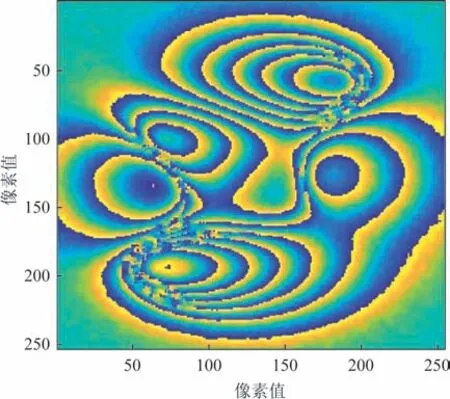
圖2 解纏前干涉Fig.2 Interference image before phase unwrapping

3.1 仿真實驗

上文中所提到的方法對干涉圖像做處理，經自適應算法選取可知高相干點位于（80～170，50～180），塊大小為90×130，將上圖保留高相干塊并依照其大小劃分其他區域，進而對其解纏繞，與從小到大隨機選取其他分塊大小做解纏對比，解纏后實驗結果如圖3 所示。圖3（a）～圖3（f）分別為尋優后分塊的解纏結果、選取分割塊大小為50×50 的解纏結果、選取分割塊大小為100×100 的解纏結果、選取分割塊大小為150×150 的解纏結果、選取分割塊大小為200×200 的解纏結果和選取分割塊大小為256×256 的解纏結果。圖3（a）～圖3（f）的解纏全流程處理時間分別為4.07、2.18、3.32、4.55、4.51 和8.92 s。

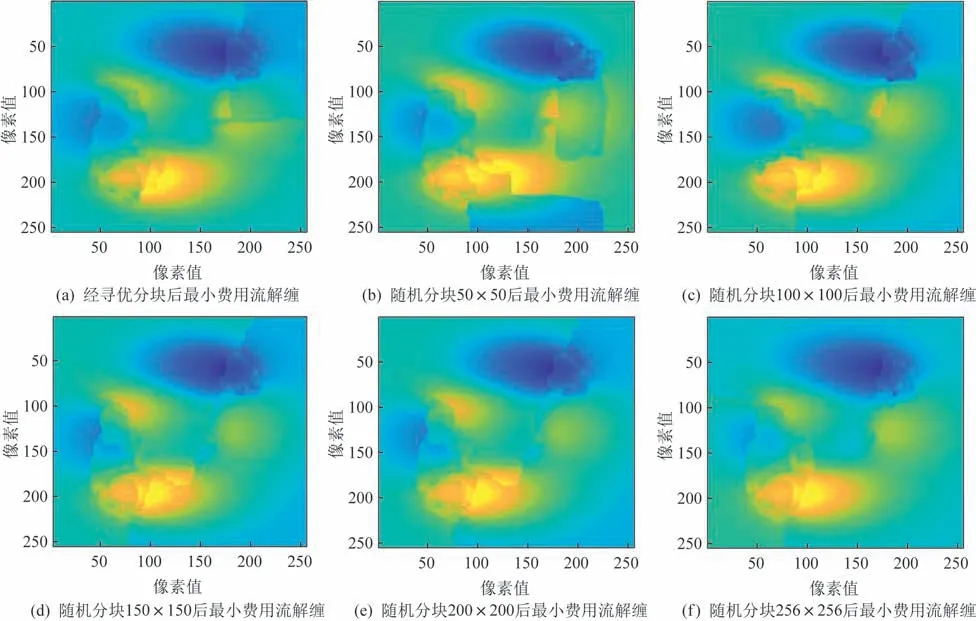
圖3 不同分塊方式解纏后圖像Fig.3 Images after unwrapping with different chunking methods

不同分塊解纏結果誤差如圖4 所示。其中圖4（a）～圖4（f）的解纏后均方根誤差（Root Mean Square Error，RMSE）分別為4.002 8、5.564 1、5.574 6、5.232 5、5.232 5 和3.962 9 rad。

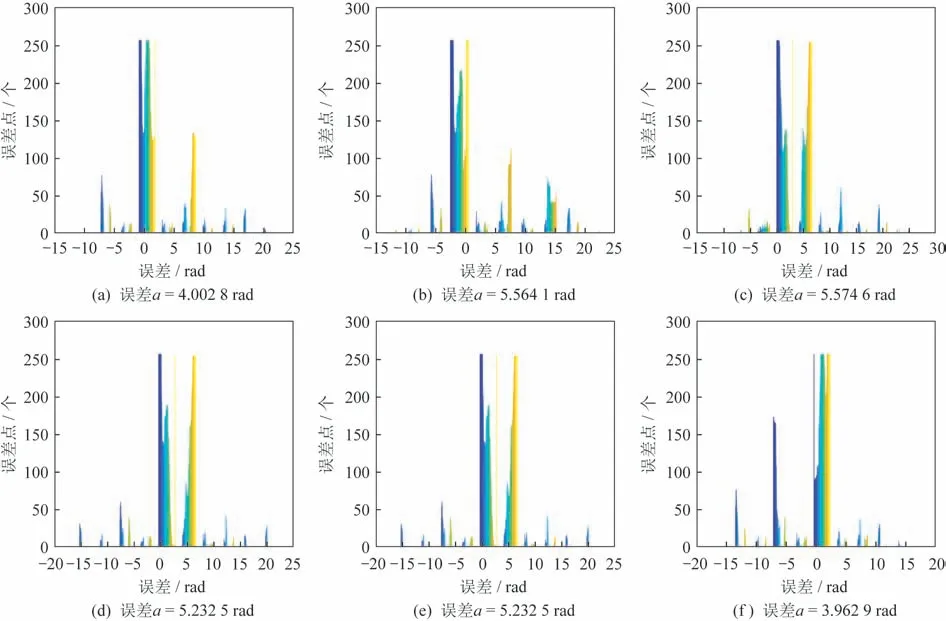
圖4 不同分塊方式解纏圖像后均方根誤差Fig.4 RMSE results after unwrapping the images with different chunking methods

仿真試驗結果統計見表1。

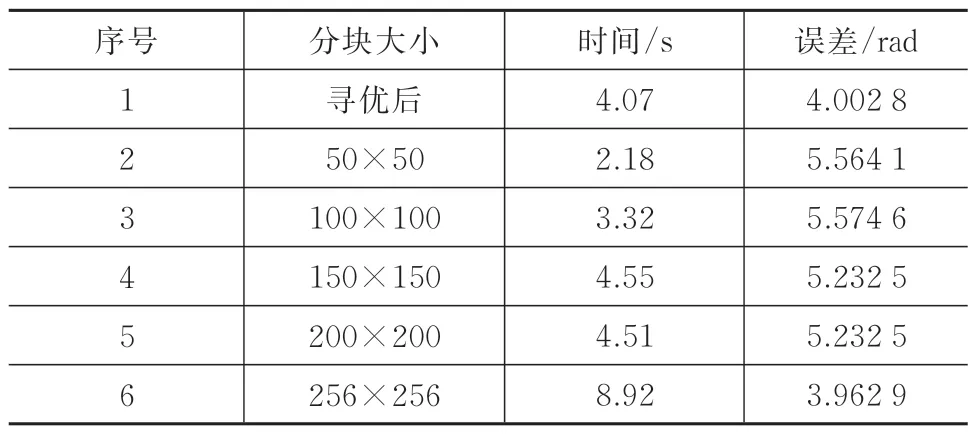
表1 仿真試驗結果Tab.1 Simulation results

3.2 結果分析

由上述仿真結果可知，采用文中算法選取到的分割大小可在4.07 s 內完成解纏，誤差為4.002 8 rad，對比其他隨機選取的分塊大小，本算法在保證解纏效率的同時，其準確度沒有大幅下滑。對比誤差最小的分塊方式（256×256），解纏誤差惡化了1.01%，但效率提升了54.37%。證明本算法在平衡效率和準確度方面具有一定的優勢，對提升改進MCF 算法的應用場景與計算效率有一定的貢獻。

4 結束語

針對改進的基于分割的最小費用網絡流算法準確率及效率受分割塊大小影響的問題，提出利用質量圖表征相干性優劣的特性自適應確定分割塊大小的方法，進而將相干性較好的區域聚集在一起，將殘差點散落地分布在不同分割塊中。仿真結果表明，本方法通過自適應尋優方式選取合適的分割塊，使得準確度在不受過多影響的情況下，有效地提高算法效率。不足之處是在分割干涉圖進行的過程中，存在將其分塊過小的可能，進而導致解纏后圖像出現較為嚴重的馬賽克現象。在后續研究中，將探究如何對自適應分塊后的圖像做針對性的解纏、融合處理。