頭針聯合下肢智能反饋訓練對卒中后下肢功能障礙患者下肢運動功能及步態的影響※
張紹華 王玉龍 章春霞 肖 鵬 何麗明 李長征
(廣東省深圳市大鵬新區南澳人民醫院康復科,廣東 深圳 518121)
卒中因其高發病率、高致殘率、高死亡率,目前已經成為全球威脅人類生命的第2殺手疾病,是成年人致殘的第1位病因[1]。而卒中后引起的步行能力下降,是影響患者回歸家庭、回歸社會的主要因素[2]。目前,卒中后下肢運動障礙的治療方法較多,包括傳統針灸、物理療法、運動療法等,但尚無特效療法,有15%~30%的患者會遺留永久性殘疾[3]。頭針作為治療卒中后運動功能障礙的有效治療方法,在既往大量的研究中已經得到了證實[4-6],但也有一些研究認為,頭針在卒中的康復治療中療效不確切[7]。部分觀點認為,頭針治療起作用的關鍵在于針刺刺激的強度及刺激時機的選擇[8]。因此,我們通過查閱國內外文獻,并結合長期康復過程中總結的經驗,將頭針與下肢智能反饋訓練相結合,借助智能化訓練系統提供的參數,為頭針的行針刺激提供參考。2017-10—2019-10,我們采用頭針聯合下肢智能反饋訓練治療卒中后下肢功能障礙患者70例,并與下肢智能反饋訓練治療70例對照,觀察對患者下肢運動功能及步態的影響,結果如下。
1 資料與方法
1.1 一般資料 全部140例均為廣東省深圳市大鵬新區南澳人民醫院康復科住院康復的卒中后下肢功能障礙患者,按照隨機數字表法分為2組。治療組70例,男35例,女35例;年齡40~75歲,平均(57.35±15.49)歲;病程55~120 d,平均(87.11±30.81)d;腦梗死38例,腦出血32例;左側肢體功能障礙38例,右側肢體功能障礙32例。對照組70例,男34例,女36例;年齡45~72歲,平均(58.90±12.35)歲;病程55~120 d,平均(89.07±30.60)d;腦梗死30例,腦出血40例;左側肢體功能障礙36例,右側肢體功能障礙34例。2組一般資料比較差異無統計學意義(P>0.05),具有可比性。
1.2 病例選擇
1.2.1 診斷標準 參照《上海市中醫病證診療常規》[9]及《各類腦血管疾病診斷要點》[10],經顱腦MRI或CT明確診斷為腦梗死或腦出血。
1.2.2 納入標準 ①首次發病,病程在180 d以內,生命體征穩定;②Brunnstrom分期在Ⅱ~Ⅴ期[10];③單側肢體功能障礙,監督或獨立狀態下可行走10 m;④意識清醒,能配合針刺及康復運行訓練;⑤年齡40~75歲;⑥患者及家屬對研究內容知情同意,均簽署知情同意書;⑦本研究經廣東省深圳市大鵬新區南澳人民醫院醫學倫理委員會審查通過。
1.2.3 排除標準 ①存在嚴重精神、心理疾病;②癲癇反復發作,存在治療風險;③有嚴重心、肝、腎等臟腑疾病;④有病毒性肝炎、結核病等傳染性疾病;⑤有凝血功能障礙;⑥顱骨缺損;⑦合并有外周神經系統疾病。
1.2.4 中止標準 ①研究過程中再發腦梗死或腦出血,需要轉神經科進行專科治療;②出現嚴重壓瘡、深靜脈血栓形成等,需要暫停治療;③懼怕疼痛,不能耐受針刺治療;④研究過程中,主動要求退出試驗的患者。
1.3 治療方法 2組均予常規運動康復訓練,如認知治療、言語訓練、吞咽訓練、手功能訓練等。
1.3.1 對照組 予下肢智能反饋訓練。操作:采用下肢智能反饋訓練系統(中國廣州一康醫療設備有限公司,型號:A1),訓練前先將患者軀干、骨盆及下肢分別綁定于儀器上,準備工作就緒后,進入主操作界面,根據患者的具體情況選擇適合的站立角度,同時設置左、右腿不同的活動范圍(0~25°),以及步頻(1~80步/min)。每日1次,每次40 min,每周治療6 d。
1.3.2 治療組 在對照組治療基礎上予互動式頭針治療。取穴:頭針選穴為頂顳前斜線(前神聰至懸厘穴)上1/5,頂顳后斜線(百會至曲鬢穴)上1/5,均取病灶側穴線,穴位定位依據《針灸學》[11]中的定位方法。患者進行下肢智能反饋訓練的同時進行頭針治療。穴位常規消毒,選用0.25 mm×40 mm一次性針灸針,針身與頭皮成15 °左右夾角快速刺入頭皮下,當針尖抵達帽狀腱膜下層、指下感到阻力減少時,使針身與頭皮平行,刺入25~35 mm,然后快速連續行捻轉手法,捻針速度保持在200次/min左右,捻針角度取決于患者的病情和耐受程度(一般在90°~360°范圍)。留針過程中囑患者隨著下肢智能反饋系統進行主動步行運動訓練。當下肢智能反饋訓練系統操作界面顯示患者用力不足時,針灸師對患者進行捻轉行針手法1次,每次2~3 min,行針1次后繼續步行訓練。每日1次,每次40 min,每周治療6 d。
1.3 療程 2組均治療8周,并隨訪8周。
1.4 觀察指標
1.4.1 主要療效觀測指標 ①采用下肢Fugl-Meyer評定量表(FMA)[12]對患側下肢進行運動功能評定,總分34分,包括17項,分數越高,下肢功能障礙越輕。②Berg平衡量表(BBS)[13],包含14個動作項目,每項0~4分,最高分為56分,分數越高平衡能力越強。③6 min步行試驗(6MWT)[14],看護下讓患者采用所能承受的最快步行速度徒步行走,測定患者6 min行走的距離。④改良Barthel指數(MBI)[15]量表,總分100分,分為進食、修飾、轉移、平地行走45 m、如廁、穿脫衣服、上下樓梯、大小便控制等10個方面,評分越高,生活自理能力越強。
1.4.2 次要療效觀測指標 采用步態功能評價系統(意大利Sensor Medica s.a.e公司)及freestep軟件(1.4.03版本)對患者進行步態參數測定,患者需在安靜的環境下進行數據采集,并進行1~2次預實驗以熟悉相關的測試流程,患者在測試時先脫去鞋子,在測試區域前2 m處開始以自然的步態在壓力傳感器板上行走,然后在2 m處停下[16]。每個患者采集3次,每次采集過程中可休息1 min,每次采集至少保證存在一個完整的步行周期,取3次測試參數的平均值進行計算和分析[17],測試參數包括步頻、步幅、步寬、患側足偏角等。
1.4.3 觀測時點 由1名經過培訓的專業人員,在治療前后及8周后隨訪時對上述觀測指標進行評估、登記,這名評估人員對患者的分組情況不知情。
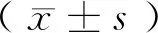
2 結 果
2.1 2組治療前后下肢FMA評分、BBS評分、6MWT距離、MBI變化比較 見表1。
由表1可見,治療后、隨訪時2組下肢FMA評分、BBS評分、6MWT距離、MBI均較本組治療前升高(P<0.05);治療后治療組BBS評分、6MWT距離、MBI評分均高于對照組同期(P<0.05),隨訪時治療組下肢FMA評分、6MWT距離、MBI評分均高于對照組同期(P<0.05)。

表1 2組治療前后下肢FMA評分、BBS評分、6MWT距離、MBI變化比較
2.2 2組治療前后步頻、步幅、步寬、患側足偏角變化比較 見表2。

表2 2組治療前后步頻、步幅、步寬、患側足偏角變化比較
由表2可見,治療后、隨訪時治療組及治療后對照組步頻、步幅均較本組治療前升高(P<0.05),步寬、患側足偏角均降低(P<0.05),隨訪時對照組步頻均較本組治療前升高(P<0.05),步寬、患側足偏角均較降低(P<0.05);治療后、隨訪時治療組步頻均高于對照組同期(P<0.05),患側足偏角均低于對照組同期(P<0.05),隨訪時治療組步幅高于對照組同期(P<0.05)。
3 討 論
卒中后下肢運動功能障礙是影響卒中患者回歸家庭和提高生活自理能力的主要因素,是卒中后遺癥康復治療的重點[18]。既往研究證實,頭針治療能夠激活大腦相關區域,促進軸突再生,在腦重塑中發揮重要作用[19]。但是,神經重塑理論認為,并非所有的重塑都是有積極意義的,如果缺少正確的康復引導和針對性的康復訓練,軸突的再生有可能會加劇不正確的運動模式和代償運動,且難糾正。在臨床康復過程中,我們發現針刺治療對卒中軟癱期的治療有明顯療效,當進入痙攣期以后,反復的針刺刺激反而會進一步加重肌肉攣縮,導致不同肌肉在力量、張力上的失衡,加劇偏癱步態形成,反而不利于運動功能的進一步恢復。著名康復醫學專家Bobath的學生Davies在《循序漸進》一書中指出:“神經元的樹狀生長源于需求”“這種生長明顯伴著新的突觸形成”[20]。基于這樣的認識,我們猜測,雖然針刺治療能夠促進中樞神經形成新的突觸,但如果沒有正確的運動治療模式引導,神經元很可能按照異常的痙攣模式生長,最終這種錯誤的運動模式不斷被強化而形成誤用綜合征。
近年來,康復機器人在卒中患者的康復中應用越來越多。本研究中的下肢智能化反饋訓練系統,通過控制患者走步時的髖、膝、踝關節,并通過影像、聲音等刺激,引導患者按照正常模式進行步行訓練。也有研究發現,康復機器人雖然能引導患者按照正確的步行運動模式進行訓練,但是長期反復的使用,會導致患者運動訓練的主動積極性下降,肌肉活性降低,反而不利于長期的康復[21]。為此,我們通過大量查閱文獻,結合治療卒中后運動功能障礙的臨床經驗,將頭針治療與下肢智能化反饋訓練系統同步進行,通過下肢智能反饋訓練系統引導患者主動進行步行訓練,同時反復捻轉行針強刺激患者頭部下肢運動及感覺區,促進患者主動運動,提高患者步行訓練主動參與的積極性。并通過下肢智能反饋訓練,為頭針的腦神經重塑提供引導作用,使卒中患者神經重塑向著對患者有利的途徑進展,這與胡曉麗等[22]的研究相一致。
卒中屬中醫學“中風”范疇。卒中恢復期及后遺癥期遺留下肢活動不利,其病機多為痰、瘀等阻滯經絡,氣血不能濡養經脈,因此治療方面當以疏通經絡為要,經絡通則經脈得以濡養,運動功能才能恢復。針刺治療卒中后肢體麻痹、萎軟是一種有效的治療方法。但是傳統針刺在治療過程中,注重醫者的操作,而患者完全被動接受,缺乏互動機制,因此針感難以到達病所。近些年的“運動針刺”理論認為,醫者行針過程中患者配合以肢體、關節的運動,有利于針感的傳遞,從而達到“氣至病所”的目的。頭針配合下肢智能反饋訓練,在頭針的同時,采用具有減輕負重、主動及被動運動功能的下肢智能反饋訓練系統,能讓患者在接受針刺刺激的同時,在減輕負重狀態下、機器輔助下進行模擬正常人的步態行走,有利于更大限度地發揮針刺療效。前期研究已經證實,頭針與下肢智能反饋訓練相結合,能有效改善卒中患者足底動態和靜態壓力分布[23-24],而本研究進一步證實,頭針聯合下肢智能反饋訓練對卒中患者下肢運動功能、平衡能力、步行能力和生活自理能力均有顯著改善作用,這與徐傳偉等[25]、汪軍等[26]的研究結果一致。傳統針灸理論認為,針刺療效的關鍵在于“得氣”,在針刺頭部下肢運動、感覺區的同時,采用下肢智能反饋訓練系統引導患者進行步行訓練,有助于幫助針感向患病部位傳遞[27-28],從而達到“刺之要,氣至而有效”的目的。通過對患者步頻、步幅、步寬及患側足偏角等步態參數的檢測,發現頭針聯合下肢智能反饋訓練能有效提高卒中患者步頻、步幅,降低步寬和患側足偏角,從而提高卒中患者步行能力及步態穩定性,這與莊燕等[29]的研究結果一致。但是本研究與這些研究相比,優勢在于采用了更為嚴謹的隨機對照試驗,為了避免因不同運動治療師手法及強度的不同,影響患者康復療效,采用了下肢智能反饋訓練系統,使所有的運動訓練采用同樣的運動模式、時間等,并依據系統顯示的參數,對患者進行運針刺激,大大降低了人為因素造成的實驗數據偏倚。
本研究從臨床觀察的角度證實了頭針聯合下肢智能反饋訓練治療卒中后下肢運動障礙的療效,但是對于其作用機制未能進行更深入的揭示。在下一步的研究中,我們將采用功能性磁共振從大腦結構與功能網絡角度進一步研究該治療方法的作用機制,為卒中后運動障礙的康復治療提供循證醫學證據。

