一種基于SRE 的對稱可搜索加密方案

黃一才 郁 濱 李森森

（信息工程大學 鄭州 450001）（huangyicai3698@163.com）

可搜索加密無需解密就能實現數據搜索.依據搜索時所采用的加密算法加密方案可分為公鑰可搜索加密（public key encryption with keyword search, PEKS）和對稱可搜索加密（searchable symmetric encryption,SSE）這2 類.其中SSE 方案因采用對稱算法，在數據量較大的云存儲環境下往往具有更高的搜索效率.

1 相關工作

2000 年，Song 等人[1]提出了可搜索加密的基本概念，并基于對稱密碼算法，構造對稱可搜索加密方案.文獻[2-6]分別構造了正排索引、倒排索引、雙向索引和樹形索引結構的對稱可搜索加密方案，提高了方案的搜索效率.

相比靜態方案，支持密文數據更新，如添加、刪除等操作的動態方案具有更好的實用性.文獻[6]利用OMAP 結構隱藏服務器密文字典的訪問地址，實現了一種安全且支持動態更新的對稱可搜索加密方案，但OMAP 結構較高的通信開銷降低了方案的實用性[7].文獻[8-10]分別采用并行計算和優化I/O 效率的方式進一步提高了方案的搜索效率.文獻[11]設計2 級索引鏈結構，實現了固定大小的客戶端存儲空間開銷.

安全性一直是動態方案構造中研究的熱點問題.為方便對動態方案的安全性進行分析，Curtmola 等人[4]通過泄露函數給出了自適應安全對稱可搜索加密方案的定義.文獻[12]給出了方案動態更新時前向及后向隱私的正式定義.文獻[13]構造了一種前向隱私的可搜索加密方案，但方案需要進行大量的指數運算，搜索效率不高.文獻[14-16]提出了執行效率更高的前向隱私方案.文獻[17-18]提出了同時滿足前向和后向隱私的對稱可搜索加密方案，文獻[19]提出了利用SGX 技術實現的后向隱私，但方案的安全性需要基于特殊軟件平臺，一定程度上降低了方案的通用性.

方案的構造過程通常需要結合應用場景在搜索效率、存儲和通信開銷、安全性、功能性等方面進行多種妥協.其中利用可穿刺加密技術構造的前向/后向隱私方案，具有交互少、安全性高的特點，近年來越來越受到人們的重視.文獻[20]基于可穿刺加密技術，在Janus 方案[12]基礎上，采用可穿刺偽隨機函數[21]代替公鑰算法，設計了對稱可穿刺可搜索加密方案Janus++，提高了方案在增加和刪除密文索引時的效率，且方案在實現后向隱私的同時，具有更小的通信開銷.

Sun 等人[22]指出Janus++方案中使用的對稱可穿刺加密（symmetric puncturable encryption，SPE）無法抵抗共謀攻擊，為此定義了基于可穿刺偽隨機函數的對稱可撤消加密（symmetric revokable encryption，SRE）密碼學原語，并利用對稱可撤消加密構造一種單輪交互的后向安全對稱可搜索加密方案Aura.Aura 方案使用GGM 樹實現可穿刺偽隨機函數，并在此基礎上引入Bloom Filter 記錄刪除索引，實現了TypeII 級后向隱私.實驗證明，該方案能夠進一步提高搜索響應速度.然而該方案存在2 個方面的不足：1）由于Bloom Filter 存在假陽性[23]，會導致索引誤刪除.2）服務器在每次搜索前需要生成所有密鑰序列，增加了服務器計算開銷，降低了搜索效率，且使非可信服務器提前掌握了所有密鑰信息，存在一定的安全隱患.

本文基于Aura 方案[22]提出了一種改進的可穿刺對稱可搜索加密方案，具有3 個方面的優勢：

1） 搜索效率高.通過在客戶端增加存儲節點使用標志，解密時僅傳輸已使用節點密鑰，減少服務器端計算開銷，提高搜索效率，且節點平均搜索時間不受節點規模影響.

2） 避免誤刪除.結合Bloom Filter 設計思想，計算可穿刺密鑰節點位置選擇算法，在提高節點利用率的同時，防止因哈希碰撞而誤刪索引.

3） 服務器密文存儲規模小.Aura 方案中密文規模與Bloom Filter 中哈希函數個數相關，通過設計插入位置選擇算法為每個索引選擇唯一的節點位置，避免密文規模擴大，減少服務器密文存儲開銷.

2 預備知識

首先簡要介紹方案設計中用到的相關密碼學基礎知識，包括多點可穿刺偽隨機函數、對稱加密算法及前向與后向隱私等.

2.1 多點可穿刺偽隨機函數

定義1.多點可穿刺偽隨機函數[21-22].設t(·)表示一個確定的多項式，密鑰空間為 K的偽隨機函數MF：K×X →Y ， 若集合S滿 足 |S|≤t，存在另外一個密鑰空間Kp以及3個多項式時間算法 （Setup,Punc,Eval）：

1）k←Setup(1λ).輸入安全參數λ，輸出偽隨機函數密鑰k∈K.

2）kS←Punc(k,S).輸 入 密 鑰k∈K ， 集 合S?X s.t.|S|≤t(λ)， 輸出可穿刺密鑰kS∈Kp.

3）y←Eval(kS,x).輸入可穿刺密鑰kS∈Kp，x∈X，輸出y∈Y 或 ⊥.

則稱MF為多點可穿刺偽隨機函數t-Punc-PRF（tpuncturable pseudorandom function）.

定義2.MF正確性[22].對所有S?Xs.t.|S|≤t(λ)，x∈XS，k←Setup(1λ)，kS←Punc(k,S)， 對 所 有k∈K使

成立，其中 ν (λ)為 可忽略函數，則稱函數MF滿足正確性條件.

2.2 對稱加密算法

定義3.對稱加密算法[22].設明文空間 M、密鑰空間 K 和密文空間 C，則對稱加密（symmetric encryption，SE）算法可用3 個多項式時間算法的三元組表示，記為S E=(Gen,Enc,Dec)，其中：

1）k←Gen(1λ).輸入秘密參數 λ ，輸出密鑰k∈K.

2）ct←Enc(k,m).輸入密鑰k、明文消息m，輸出密文ct∈C.

3）m←Dec(k,ct).輸入密鑰k、密文ct，成功解密輸出ct對應明文m， 否則輸出 ⊥.

定義4.SE正確性[22].若算法對任意明文m∈M，k←Gen(1λ)且ct←Enc(k,m)，滿足

則稱算法SE滿足正確性條件.

2.3 前向隱私與后向隱私

可搜索加密方案前向隱私是指更新查詢不會泄露正在更新的關鍵字或文檔對中所涉及的關鍵字信息，主要針對文檔添加操作，確保新添加文檔不會包含在以前查詢令牌的檢索結果中.文獻[24]指出針對不具備前向隱私的方案可有效實施文件注入攻擊，快速恢復用戶檢索信息.

后向隱私要求搜索和更新操作僅泄露數據庫中的當前文檔（不包括已刪除的文檔），主要針對文檔刪除操作，確保當前查詢不會包含過去已刪除的文檔索引.文獻[4]根據泄露信息不同，將安全強度由高到低分為TypeⅠ，TypeⅡ，TypeⅢ.TypeⅠ后向隱私允許泄露當前關鍵詞所匹配的文檔索引、插入時間及更新關鍵詞的更新總數；TypeⅡ在TypeⅠ基礎上，增加了泄露關鍵詞的操作類型和時間；TypeⅢ相對于TypeⅡ，增加了泄露刪除操作對應的那個添加操作.

3 搜索模型

本文方案中各主要符號定義如表1 所示.為簡化方案構造，假定：

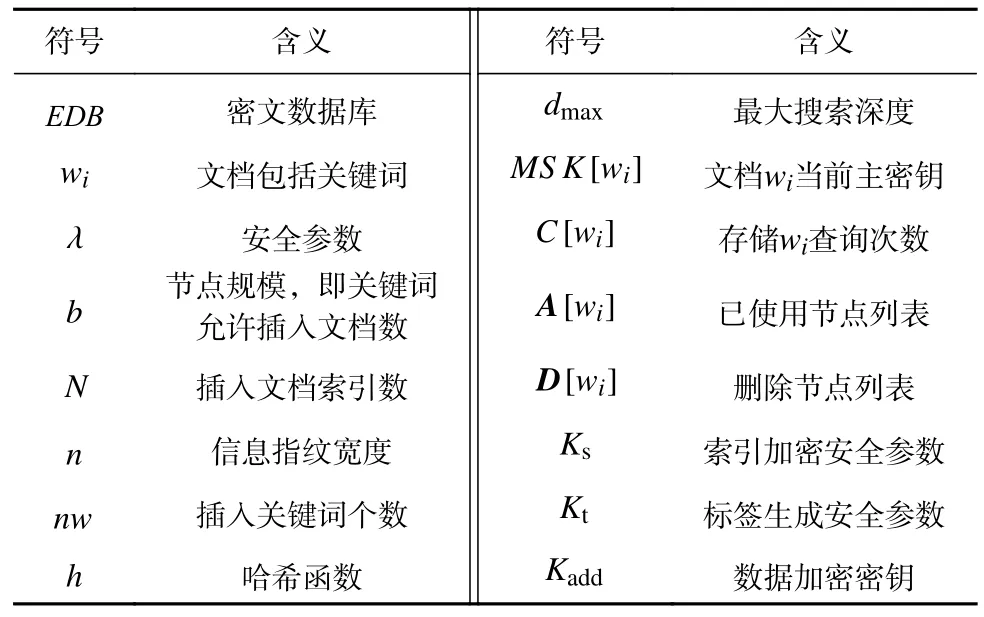
Table 1 Symbol Definition表1 符號定義

1）服務器為“誠實且好奇（honest but curious）”的.即服務器能忠實運行用戶發出的請求，但也會盡可能地窺探用戶個人隱私.

2）只有數據擁有者（data owner，DO）是完全可信的，且能夠訪問系統中所有的明文信息；各實體之間以及云存儲服務器內部各通信信道均不可信，且存在各種可能的網絡攻擊行為.

3）數據擁有者能夠對文檔進行解密，但在訪問服務器前并不確定云服務器中存有哪些文件，以及是否包含其想要的文件.

4）不考慮多客戶端應用場景.僅對方案搜索效率優化與避免誤刪除進行設計，對多客戶端場景下的特殊性不做專門研究.

3.1 場景描述

對稱可搜索加密應用場景由安全存儲服務器和數據擁有者2 部分組成，其中安全存儲服務器包括1個存儲用戶密文文件的存儲服務器和1 個實現數據密文搜索的密文索引搜索服務器.DO 既能夠向安全存儲服務器中添加新的密文文件，又可以實現對數據密文查詢.應用場景如圖1 所示.

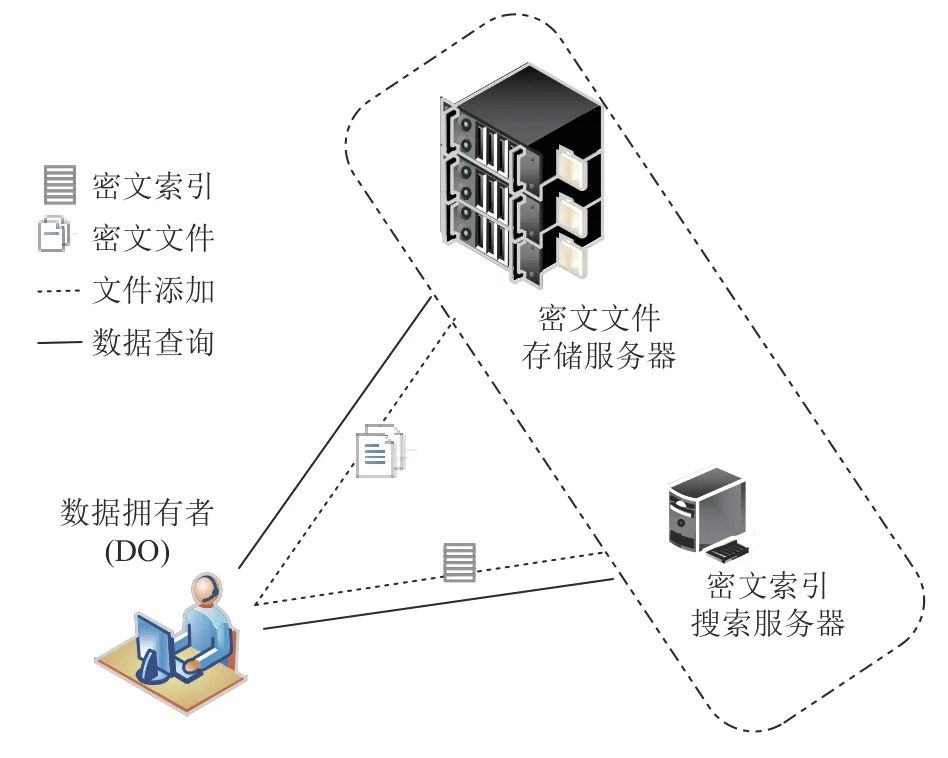
Fig.1 Application scenario of dynamic searchable symmetric encryption圖1 動態對稱可搜索加密應用場景

方案的工作過程包括數據動態更新和數據查詢2 個階段，其中數據動態更新通常包括數據添加、刪除和更新3 種操作，為簡化描述過程，這里以數據添加為例，具體描述方案的工作過程.

1）數據添加.用于向密文索引數據庫中加入新的數據文件索引.DO 先將數據文件加密后存儲在文件存儲服務器，并返回訪問入口信息；然后DO 通過對明文數據進行處理，生成文件訪問入口信息與關鍵詞對應關系，并按照一定索引結構生成密文索引，將密文索引存儲于密文索引服務器.

2）數據查詢.要求密文服務器不用解密具體密文文件，便能從所有密文文件中返回符合用戶查詢需求的文件信息，這也是可搜索加密方案的核心.此過程一般是DO 通過關鍵詞生成查詢令牌，然后通過密文索引服務器獲取密文文件的入口地址信息，最終從密文文件服務器獲取密文文件.

3.2 方案形式化描述

動態對稱可搜索加密（dynamic searchable symmetric encryption, DSSE）的形式化定義通常由一組多項式時間算法組成.

定義5.DSSE 方案.設數據庫由DB=文檔地址或關鍵詞集構成，其中idi為第i文 檔，Wi為文檔i包含的關鍵詞集合，d為數據庫中文檔的數量，則動態對稱可搜索加密方案可用一個三元組多項式時間算法(Setup,Search,Update)表示，其中：

1）初始化算法：(K,σ,EDB)←S etup(1λ,DB).算法輸入安全參數 λ和明文索引數據庫DB， 輸出密鑰K、關鍵詞狀態 σ和密文索引數據庫EDB.在DSSE 方案中，通常設EDB=?.

2）查 詢 算 法：(DB(w),σ′,EDB′)←S earch(K, σ,w;EDB).輸入密鑰K、關鍵詞狀態 σ和檢索關鍵詞w，輸出包含檢索關鍵詞w的所有文檔標識DB(w)，以及搜索操作后關鍵詞狀態 σ′和密文索引數據庫EDB′.通常算法包含客戶端生成查詢令牌和服務器根據令牌搜索查詢結果2 部分.

3）更新算法：(σ′,EDB′)←Update(K,σ,w,ind,op;EDB).輸入密鑰K、關鍵詞狀態 σ、更新關鍵詞w及對應索引ind，更新操作類 型op，其中op∈{add,del}，輸出更新后的密文索引數據庫EDB′、 關鍵詞狀態 σ′.

定義6.DSSE 正確性[25].對于所有的DB和W，若任意的w∈W，滿足

則稱DSSE 方案滿足正確性條件.

3.3 SRE 語法定義

定義7.SRE 算法定義[21].設 MSK表示密鑰空間，T表示標簽空間，則一個SRE 算法可用4 個多項式時間算法表示，記為SRE=(KGen,Enc,KRev,Dec)，其中：

1）msk←KGen(1λ).輸入安全參數 λ，輸出系統密鑰msk∈MSK.

2）ct←Enc(msk,m,T).輸入系統密鑰msk，消息m∈M 及 標簽列表T?T ，輸出消息m標 簽T下的密文ct.

3）skR←KRev(msk,R).輸入系統密鑰msk及撤消列表R?T ，輸出撤消后的密鑰skR，僅能解密不屬于標簽R對應的密文.

4）m←Dec(skR,ct,T).輸入撤消后的密鑰skR、密文ct及對應標簽T，輸出消息m（ 解密失敗輸出 ⊥）.

定義8.SRE正確性.對所有安全參數 λ ∈N+，消息m∈M 及 對應標簽T?T 、撤消列表R?Ts.t.R∩T=?，算法SRE正確解密的概率Pr[SRE.Dec(skR,ctm,t)=m]=即對于未撤消加密節點均可正確解密，則稱算法S RE滿足正確性條件.

相比文獻[21]給出的正確性定義中，解密發生錯誤的概率以一個不可忽略函數 ν (λ)為上界，定義8要求能夠對t∈T 且t?R的 所有密文ctm及對應標簽T，均可正確解密.

定義9.撤消操作.對所有安全參數 λ ∈N+， 消息m對應標簽t∈Ts.t.T?T 和撤銷列表R?T ，消息m∈M，撤消加密操作定義為R=R∪{t}.

性質1.撤消操作的有效性.對所有安全參數λ ∈N+， 消 息m對 應 標 簽t∈Ts.t.T?T 和撤 銷 列 表R?T ，消 息m∈M 撤 消 加 密，則Pr[S RE.Dec(skR,ctm,t)=m]=0 ， 即撤消加密后無法通過撤消后的密鑰skR、密文ctm和對應標簽t完成解密.

證明.令消息m撤消前的撤消列表為R′，根據定義9，撤消后撤消列表R=R′∪{t}， 則有t∈T 且t∈R.

根據正確性定義，Pr[S RE.Dec(skR,ctm,t)=m]=0.

證畢.

性質2.撤消操作的正確性.對所有安全參數λ ∈N+， 已 插 入 消 息 M={m1,m2,···,mn}，對 應 標 簽T={t1,t2,···,tn} 和 撤銷列表R?T ，其中n為已插入消息 數.?mi,mj∈M ， 對 應 標 簽 分 別 為ti,tj∈Ts.t.i≠j,ti≠tj.當ti∈R,tj?R，則

Pr[SRE.Dec(skR,ctmi,ti)=mi]=0且Pr[SRE.Dec(skR,ctmj,tj)=mj]=1，即撤消解密后不會破壞其他已加密密文解密的正確性.

證明.因為ti∈R，由性質1 可知，Pr[S RE.Dec(skR,ctmi,ti)=mi]=0成立.

因為tj∈T且tj?R， 則由定義8 可知，Pr[S RE.Dec(skR,ctmj,tj)=mj]=1成立.證畢.

撤消消息m∈M 對 應密文ctm的 解密操作，將ctm對應標簽tm加入撤消列表，即進行消息刪除操作.

定理1.誤刪除條件.若方案滿足正確性條件，發生誤刪除的充要條件是 ?j≠i,且ti=tj.

證 明.設 ?mi,mj∈M ，對 應 標 簽 分 別 為ti,tj∈Ts.t.i≠j，mi撤 消前撤消列表為R*.

1） 充分性

設消息mi撤 消后，mj也 被撤消，其中j≠i,ti≠tj.撤消前，ti,tj∈T 且ti,tj?R*.當mi撤消后，依據性質2，撤消列表R=R*∪{ti}.

因 為j≠i且ti≠tj，tj?R*，所 以tj?R*∪{ti}=R, 則Pr[SRE.Dec(skR,ctmj,tj)=mj]=1.

因為mi撤 消時，mj也被撤消，所以依據性質1，有Pr[SRE.Dec(skR,ctmj,tj)=mj]=0.

矛盾，即假設不成立.

2） 必要性

由定義9 得到，刪除mi后 ，撤消列表R=R*∪{ti}，即ti∈R.因為ti=tj， 所以tj∈R.

根據正確性定義，可得

則由定義9 可知，消息mj也已刪除.證畢.

可以看出，防止選擇相同標簽加密是避免誤刪除的有效手段.

4 方案構造

插入位置選擇算法為每個插入文件索引尋找唯一的節點位置.在此基礎上，構造基于SRE 的對稱可搜索加密方案.

4.1 插入位置選擇算法

插入位置選擇算法用于在給定范圍內，為消息m隨機選擇一個未使用的節點位置pm.

設hp(x)，hf p(x)分 別表示2 個 哈希函數，Lb表示長度為b的狀態列表，Lb[i]=(fi,f pi).其中，fi為占用標志，寬度為1 b，用于記錄列表Lb中位置i的占用情況，占用時標志置為 t rue， 否則置為false；f pi為 位置i上存儲的消息指紋，一般為消息m的哈希值低n比特（n為預設指紋寬度）.圖2 所示為消息m選擇插入位置過程示意圖.

Fig.2 Design idea of insertion position selection algorithm圖2 插入位置選擇算法設計思想

算法記為InsPos（b,dmax,n）， 其中b表示列表規模，dmax表示最大搜索深度，n表示消息指紋寬度，且b,dmax,n∈N+，dmax＜b，則 算 法 可 以 用 一 個 三 元 組InsPos=(S etup,Insert,Test)表示.

1）初始化：Lb←S etup(b,n,Lbinit).輸入列表規模b、初始狀態Lbinit， 輸出狀態列表Lb.工作過程為：

① 分配位長為b+nb的 比特狀態列表Lb.

②若Lbinit=⊥， 令Lb[i]=(false,⊥)， 否則Lb[i]=Lbinit[i]，其中0 ≤i≤b-1.

③ 返回比特列表Lb.

2）插入點位置選擇：(Rst,pm,Lb′)←Insert(m,dmax,Lb).輸入待插入消息m、 最大搜索深度dmax、狀態列表Lb；輸出為插入結果Rst、 插入位置pm、插入后狀態列表Lb′.工作過程為：

① 計算消息m的插入位置pm=hp(m)modb，f pm=hf p(m).

②令Rst=false ，若fpm=false， 則Rst=true，運 行③，否則 ? ≤i≤dmax，使fpm=false 成 立（其中pm=(pm+i)modb） ，則pm=(pm+i)modb，Rst=true.

③ 若Rst=true ，則 修 改Lb列 表fpm=true，f ppm=f pm.

④ 返回插入結果Rst、 插入位置pm、最新狀態列表Lb′=Lb， 即 (Rst,pm,Lb′).

當Rst=true時表示在列表中找到唯一的節點位置pm， 否則表示在搜索深度d=dmax下未能找到空閑節點，返回pm為第1 哈希的節點位置.此時若選擇此節點位置偽隨機數作為加密密鑰，將導致密鑰重用，并在刪除該節點時因同時刪除多個文件加密密鑰而造成誤刪除.

3）插入位置測試：(rstPos,f pm)←Test(m,dmax,Lb).通過對消息指紋對比獲取消息m在 列表Lb中的位置.輸入為消息m、最大搜索深度dmax、 狀態列表Lb；輸出為消息m插入位置rstPos，消息指紋f pm.工作過程為：

① 計算消息m的插入位置pm=hp(m)modb和消息指紋f pm=hfp(m).

②令rstPos=-1， 若 ?0≤i≤dmax，Lb[(pm+i)modb]=(rstPos,f pm)， 則rstPos=(pm+i)modb.

③ 返回 (rstPos,f pm).當rstPos≥0時，表示找到消息m的插入位置.

在可搜索加密方案構造中，Test算法主要用于從列表刪除索引時查找索引準確位置.搜索時服務器通過存儲密文對應標簽，直接獲取節點在列表中的位置，因此不需要重新通過Test算法計算.Test算法的性能僅影響節點刪除時的執行速度，不影響添加和搜索效率.

插入指紋生成時使用的哈希函數、位置選擇以及位置深度搜索時使用的哈希函數可以設為相同也可以設為不同，列表占用標志fi可以通過判斷指紋位置是否為0 判斷該位置是否已被占用.然而指紋生成時采用哈希函數的質量將直接影響方案指紋大小設定，選擇優秀的哈希函數作為消息指紋生成算法能有效降低指紋占用空間的大小.同時方案中，由于fi僅需1 b，占用空間較小，且能夠方便對指定位置占用情況進行判斷，提高算法執行效率.

4.2 SRE的一般構造

設S E=(Gen,Enc,Dec)為標準對稱加密算法，其密鑰空間為 Y，MF：K×X →Y為多點穿刺偽隨機函數，記 為MF=（S etup,Punc,Eval）[20-21]，InsPos（b,dmax,n）=(S etup,Insert,Test)表示插入位置選擇算法，則對稱可撤消加密算法S RE=(KGen,Enc,KRev,Dec)的具體描述為4 個步驟.

1）msk←KGen(1λ,b,n,Lbinit)： 輸入安全參數 λ和整 數b,n∈N+，Lbinit[i]=(false,⊥)， 其中0 ≤i≤b-1，系統主密鑰msk的生成過程有2 步：

①生成Lb←InsPos.Setup(b,n,Lbinit).

②生 成sk←MF.Setup(1λ)， 輸 出msk=(sk,Lb).

2） (ctm,t)←Enc(dmax,msk,m,t).輸入msk=(sk,Lb)和消息m∈M對 應標簽t∈T，通過2 個步驟生成密文ctm：

① (Rst,t)←InsPos.Insert(m,dmax,Lb)和skt=MF(sk,t).

② 生 成ctm=S E.Enc(skt,m)， 返 回 密 文ctm和 對 應標簽t.

3）skR←KRev(msk,R).輸入msk=(sk,Lb)和撤消標 簽 列 表R={t1,t2,…,tτ}， 滿 足 τ ≤NL，NL為Lb中 已使用節點數.通過2 個步驟生成R下撤消的密鑰skR：

① 計算Lb所 有置1 的索引節點位置集合IR={t:t∈[b]且t?R}.

② 計算集合skIR←MF.Punc(sk,IR)， 返回skR=(skIR,IR).

4）m←Dec(skR,ctm,t).輸入密文ctm、 對應標簽t，以及R下撤消后的密鑰skR，按2 個步驟恢復消息：

① 若t?IR，解密失敗，運行②.

② 若t∈IR， 計 算skt=MF.Eval(skI,t) ， 計 算m=S E.Dec(skt,ctm).

4.3 方案描述

設Σadd=(S etup,S earch,Update)為一個前向安全的對稱可搜索加密方案，用于動態增加密文索引，并保證前向數據隱私，SRE=(KGen,Enc,KRev,Dec)為對稱可撤消加密算法（構造方法詳見4.2 節）.算法1詳細描述 基于SRE和 Σadd的可搜索 加密方 案Σadd=(S etup,S earch,Update)的工作過程.

算法1.初始化Σ.Setup(1λ).

輸入：安全參數 λ；

輸出：密鑰集K，關鍵詞狀態 σ，密文索引數據庫EDB.

客戶端：

①(EDBadd,Kadd,σadd)←Σadd.S etup(1λ)；

③return((Kadd,Ks,Kt),(σadd,MS K,C,A,D),(EDBadd,EDBcache)).

初始化完成后，客戶端存儲密鑰K=(Kadd,Ks,Kt)、關鍵詞狀態 σ =(σadd,MS K,C,A,D)，服務器存儲密文索引數據庫EDB=(EDBadd,EDBcache).

算法2.查詢 Σ.S earch(K,w,σ;EDB).

輸入：客戶端輸入密鑰集K，關鍵詞狀態 σ，查詢關鍵詞w，服務器輸入密文索引數據庫EDB；

輸出：匹配結果集DB(w)及 更新后關鍵詞狀態 σ′.

Step 1.生成查詢令牌 Σ.S earch(K,w,σ;EDB).

客戶端：

①c←C[w],mskw←MS K[w],D←D[w],

A←A[w]；

② ifc=⊥ then

③ return ?；

④ end if

⑤ 計算skR=(skA,A)←S RE.KRev((mskw,A),D)；

/*A來自A[w]，D來自D[w]*/

⑥發送skR和tkn=h(Ks,w)至服務器；

⑦←S RE.KGen(1λ,A)；

/*搜索后更新w對應的msk*/

⑧MS K[w]←，C[w]←c+1.

Step 2.Σ.S earch(K,w,σ;EDB)結果搜索.

客戶端 & 服務器：

① 運行 Σadd.S earch(Kadd,w||i,σadd;EDBadd)，服務器得到關于密文和標簽對的列表((ct1,t1),(ct2,t2),···,(ct?,t?)).

服務器：

② 服務器使用skR按如下步驟解密所有密文{(cti,ti)}；

③ fori∈[1,?] do

④indi=S RE.Dec(skR,cti,ti)；

⑤ ifindi≠⊥ then

⑥NewInd←NewInd∪{indi,ti}；

⑦ else

⑧DelInd←DelInd∪{ti}；

⑨ end if

⑩ end for

?OldInd←EDBcache[tkn]；

?OldInd←OldInd{(ind,t):

?ti∈DelInds.t.t=ti}；

?Res←NewInd∪OldInd,

EDBcache[tkn]←Res；

? returnRes.

查詢算法用于實現對關鍵詞w的搜索操作，主要包括客戶端生成查詢令牌和結果搜索2 個步驟，即生成查詢令牌和結果搜索.

1） 查詢令牌生成.查詢令牌生成算法在客戶端運行，輸入 (K,w,σ)， 通過查詢本地MS K,C,A,D的值，生成查詢令牌tkn和 穿刺密鑰skR，并發送到服務器.

Step1 中，客戶端執行行①～⑥，根據待查詢的關鍵詞w，從MS K獲取密鑰mskw， 使用S RE算法生成撤消加密密鑰skR，使用偽隨機函數F生成查詢令牌tkn，將(tkn,skR)發送至密文索引服務器.執行行⑦⑧，更新本地存儲狀態 σ，隱藏查詢特征.同時由于行⑦⑧與Step2 在時間上可并行執行，并不會對查詢效率造成明顯影響.

2） 結果搜索.服務器接收到查詢請求，解析查詢令牌tkn和 穿刺密鑰skR，運行 Σadd搜索算法查詢密文索引數據庫EDB， 獲取關鍵詞w未穿刺節點所有密文索引，將搜索結果返回客戶端.

Step2 中，通 過 調 用 Σadd方 案 的 Σadd.S earch和S RE算法，計算查詢關鍵詞w相關的索引，去除已刪除索引，更新服務器端結果緩存EDBcache，并向客戶端返回查詢結果.

算法3.更新 Σ.Update(K,σ,op,w,ind;EDB).

輸入：客戶端輸入密鑰集K、關鍵詞狀態 σ、操作類型op、更新關鍵詞w及對應文檔索引ind，服務器輸入為密文索引數據庫EDB；

輸出：更新后的關鍵詞狀態 σ′，密文索引數據EDB′.

客戶端：

①mskw←MS K[w]，i←C[w]，D←D[w]，A←A[w]；

②ifmskw←⊥then

③ (mskw,A)←S RE.KGen(1λ) ；

④MS K[w]←mskw，D[w]←D；

⑤i←0，C[w]←i；

⑥ end if

⑦ ifop=add then

⑧ 計算 (rst,t,A′)←FKt(w,ind)，InsPos.Insert(w,dmax,A)；

⑨ct←S RE.Enc(dmax,(mskw,A),ind,t)；

⑩A←A′； /*更新添加列表*/

? 運行Σadd.Update(Kadd,add,w||i,(ct,t),σadd;EDBadd)； /*客戶端&服務器運行*/

? else(i.e.,op=del)

?D←D[w]；

? ifposw≥0 then

?D′=InsPos.Insert(w,dmax,D)；

?D[w]←D′； /*更新刪除列表*/

? end if

? end if

數據更新包括插入和刪除2 類，即op=add和op=del.

插入文檔索引時，客戶端查找主密鑰列表，找出w對應密鑰信息，利用節點位置選擇算法查找插入點位置，并利用SRE.Enc算法對索引進行加密，修改本地密鑰位置使用標志.將密文和標簽對 (ct,A)發送至服務器，服務器運行 Σadd.Update算法更新密文索引數據庫EDB.

刪除文檔索引時，通過InsPos.Test查找需要刪除的節點位置，并在刪除列表記錄刪除標記，在下次生成搜索密鑰時對應位置密鑰進行穿刺，服務器因無法恢復對應節點密鑰信息而無法解密，從而實現后向隱私.

5 方案分析

下面從插入位置選擇算法和搜索方案分析2 個方面對方案進行理論分析.

5.1 插入位置選擇算法分析

需要記錄每個位置使用情況，至少需要1 b，對于一個節點規模為b列表，算法工作時需要分配b比特存儲空間.插入時的時間復雜度為多項式時間O(n).為了進一步對算法的性能進行評價，現給出節點利用率定義.

定義10.節點利用率.當InsPos.Insert(x,dmax,Lb)首次輸出Rst=false 時，節點利用率 ρ=N/b，其中N為Lb中元素為1 的個數.

由定義10 可以看出，因為0 ＜N≤b， 所以0 ＜ρ ≤1.隨著搜索深度dmax的增大，插入點生成時間增大，空間利用率逐步升高.當dmax=b時，搜索插入點位置時間最長，節點利用率 ρ=1.在實際方案構造過程中，提高節點利用率可有效減小節點規模、減少搜索時的通信開銷.

由定理1 可知，插入消息mi后導致發生誤刪除的概率與消息mi在 插入位置選擇算法中Rst=false的概率相等.當最大搜索深度為dmax時 ，第i（i∈[b]）次選擇插入位置時InsPos.Insert算法輸出發生Rst=false的概率等于Lb在pm后 連續dmax+1個節點為1 的概率.

設位置選擇時每次均是從空余節點中隨機選擇一個位置，則設指紋長度足夠的情況下，節點規模為b、搜索深度為dmax的 列表在第N+1(N≥dmax)次插入失敗的概率為

5.2 搜索方案分析

結合本文方案的實現過程，從搜索效率、存儲開銷、通信開銷和安全性等方面進行分析.

1）搜索效率

搜索時服務器僅需要計算使用的密鑰節點，相比每次均需要計算GGM 樹所有節點密鑰的Aura 方案，平均搜索時間更低.實際上GGM 樹節點計算隨著節點規模的擴大而迅速增加，在節點規模較大、但使用節點較少的場景中，每個索引平均搜索時間將迅速增加.本文方案平均搜索時間受節點規模影響較小，在節點規模較大但使用節點較少時具有明顯的優勢.

2）存儲開銷

客戶端需要為每個節點存儲指紋、使用標志、刪除標志，通常使用標志和刪除標志僅需1 b 存儲空間，則客戶端需要預先為每個節點分配n+2比特存儲空間，其中n為每個節點指紋寬度.

服務器中需要存儲索引密文和節點位置信息，相比Aura 中密文大小為索引密文大小的整數倍，不會導致密文規模擴張，存儲空間占用更低，如表2 所示.

Table 2 Scheme Comparison表2 方案對比

3）通信開銷

本文方案采用文獻[22]的節點壓縮算法對傳輸節點進行壓縮，但與Aura 刪除前僅需傳輸單個節點信息不同，由于每次選擇節點位置是隨機的，在插入文檔索引較少時，節點壓縮率也較低，隨著使用節點數量增多，傳輸節點數量將逐步降低.

在刪除索引時，Aura 由于中間使用的索引位置被刪除，通常需要發送更多的節點.

4）安全性

本文方案通過在服務器端增加EDBcache保存上次查詢結果，并在每次查詢后更新查詢密鑰，以保護數據訪問特征.下面通過真實游戲Real和理想游戲Idea對方案安全性進行證明.

RealΣA(k).攻 擊 者 A選 擇 數 據 庫DB，DO 運 行S etup(DB)算法生成檢索索引EDB并發送給攻擊者.A按一定規則選擇一系列查詢q， DO 運行Trapdoor(q)算法生成的 Tq并發送給 A.服務器運行Search(EDB,將運行的所有結果發送給A.最后， A輸出一個比特b.

IdeaΣA,S.模擬器初始化查詢數組q.A 選擇數據庫DB，DO 運行 S(L(DB))算法生成檢索索引并發送給A.接著， A 按一定規則的選擇查詢q.模擬器記錄下查詢q[i]， 運行S(L(q,DB)).最后， A 輸出一個比特b.

定理2.方案 Σ后向隱私自適應安全.設sp(w)為關鍵詞w的搜索特征，TimeDB(w) 表 示關鍵詞w有關索引（去除刪除索引），DelTime(w) 表示關鍵詞w上的刪除操作的時間戳，方案 Σ的泄露函數 LBS定義為

其中：

若 Σadd為前向自適應隱私的對稱可搜索加密方案，SRE 滿足IND-sREV-CPA 安全，則方案 Σ為隨機預言機模型下對所有多項式時間攻擊者 A是TypeⅡ后向隱私自適應安全的.

證明.設多項式時間攻擊者 A在模擬器S中所取得的最大優勢記為AdvA,S(λ)，Gi表 示Gamei，Pr[E]表示事件E發生的概率.證明定理2的關鍵是針對自適應A構造一個高效的模擬器S，使得Pr[=1]-(λ)成 立，其中(λ)是可忽略的.

利用構造法，從真實游戲構造一個滿足要求的高效模擬器S，進而證明定理2.

Game 0.G0為 完全按照方案 Σ運行的真實游戲，則有

Game 1.在G0基 礎上，將偽隨機函數F使用隨機數代替，并將生成的隨機數存入數組中，在下次調用時重新找出生成的隨機數.在攻擊者視野下，相同的輸入均會獲得相同的隨機數.

由于偽隨機函數計算上具有不可區分性，不防設使用真隨機數代替函數F，對所有多項式時間攻擊者B1獲 得 的最 大 優 勢 為(λ) ，其 中(λ)是可忽略函數.

方案 Σ中每次新加入的關鍵詞和生成密文標簽均采用隨機數代替，則攻擊者B1能夠獲得2 倍的優勢，即

Game 2.在G1基 礎上，將前向安全SSE 方案Σadd使用模擬器代替，同時在服務器端維護一個更新操作列表Ladd，在攻擊者發出查詢操作時再執行更新操作.由于 Σadd滿足前向隱私，更新操作不會泄露關鍵詞和索引的有關信息.

Ladd包 含了方案 Σ 搜索時泄露的信息，即搜索特征sp(w) 、 索引密文及對應標簽、更新時間u.Ladd反映了關鍵詞w通過方案 Σadd執行添加操作更新的歷史記錄，并作為方案 Σadd的模擬器的輸入.針對方案 Σadd的多項式時間的攻擊者Badd，存在一個模擬器，滿足

其中(λ)是可忽略的.

Game 3.在G2基礎上，在執行可穿刺加密操作前將已刪除文檔索引置為0.由于SRE 是IND-sREVCPA 安全的[22]，因此對攻擊者B3存在一個高效的模擬器SSRE，滿足

其中(λ)是可忽略的.

Game 4.使用更新列表獲得泄露信息TimeDB和DelHist，重建索引添加列表Ladd、 使用標志A和刪除標志D，并作為模擬器的輸入.若假設每個文檔索引只會被添1 次和刪除1 次，則標簽不會被重復使用，也就不必為了保證一致性而為每個密文索引存儲對應的密文標簽.

在G4中，僅對模擬器的工作方式進行了修改，即

為構造理想游戲的模擬器，不能直接調用關鍵詞w，而改用查詢特征sp[w] 來生成令牌信息.同時，不再保持維護更新記錄的列表，而是利用搜索查詢中的泄露信息TimeDB(w)，DelTime(w)重建添加列表Ladd和 節點使用標志A、 刪除標志D.這樣利用 LBS有關信息，構造了一個高效的模擬器S，使得

將以上多項式時間攻擊者B1，Badd，B3對 方案 Σ攻擊所獲得的優勢相加，可得

其中(λ)是可忽略的，即定理2 成立.證畢.

6 方案測試

方案性能測試所采用的軟/硬件環境配置如表3所示.

Table 3 Environment Configuration of Software/Hardware for Testing表3 測試軟/硬環境配置

6.1 插入點位置選擇算法測試

插入點位置選擇算法中，消息位置、消息指紋所使用的哈希函數均采用SpookyHash V2 算法，隨機生成消息m，發生第1 次插入失敗（即未找到可用節點或發生指紋沖突）時，每個搜索深度下隨機生成500組索引，節點利用率 ρ的平均值隨指紋寬度n和搜索深度dmax的變化關系如圖3 所示.

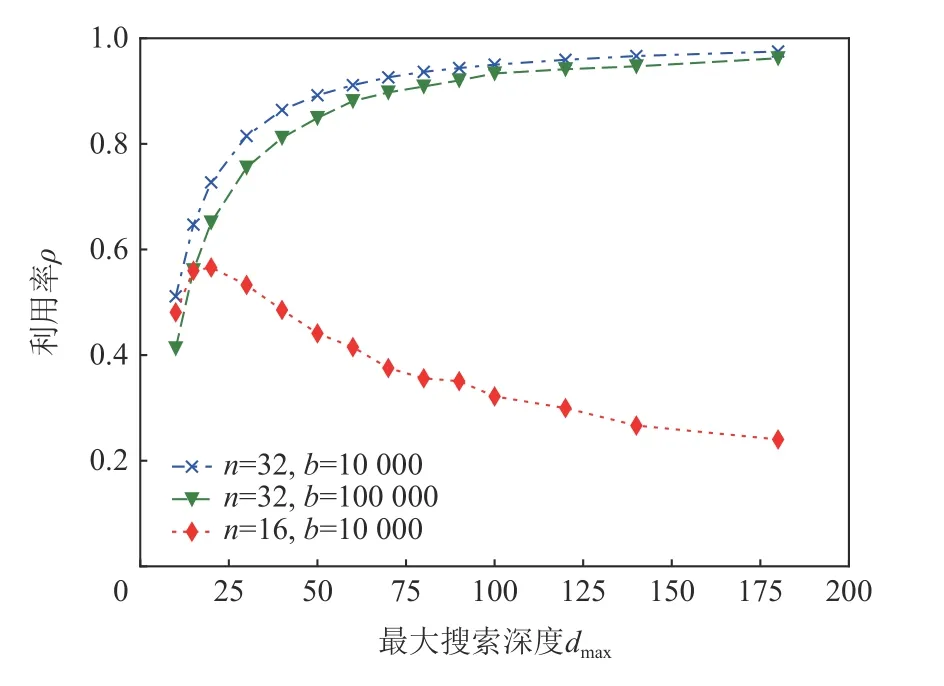
Fig.3 The curve of node utilization rate圖3 節點利用率曲線

可以看出，在n=32，dmax=100時能夠保證較高的節點利用率.

6.2 搜索方案性能測試

對稱加密算法采用AES，哈希算法選用計算速度較快的SpookyHash V2，偽隨機數發生器采用GGM 算法實現，采用支持分布式部署的非關系數據庫rocksDB 作為密文索引數據庫.測試中，隨機生成文檔索引，利用 Σ.Update算法添加至密文索引數據庫.

如表4 所示，從存儲空間開銷可以看出，Aura 在服務器中因需要同時存儲多個密文備份，服務器占用空間開銷更大.相比Aura 方案，本文方案每個密文索引不存在密文擴展，實際平均每條索引占用存儲空間開銷更小.在客戶端，密文刪除操作需要為每個節點存儲一個指紋，存儲客戶端存儲空間開銷為O(b).節點實際占用空間包含了rocksDB 內部存儲結構數據，方案實際占用的空間相比測試值要更小.另外，采用質量更好的指紋哈希算法，降低每個節點的指紋長度，也可進一步快速降低客戶端中存儲空間的大小.

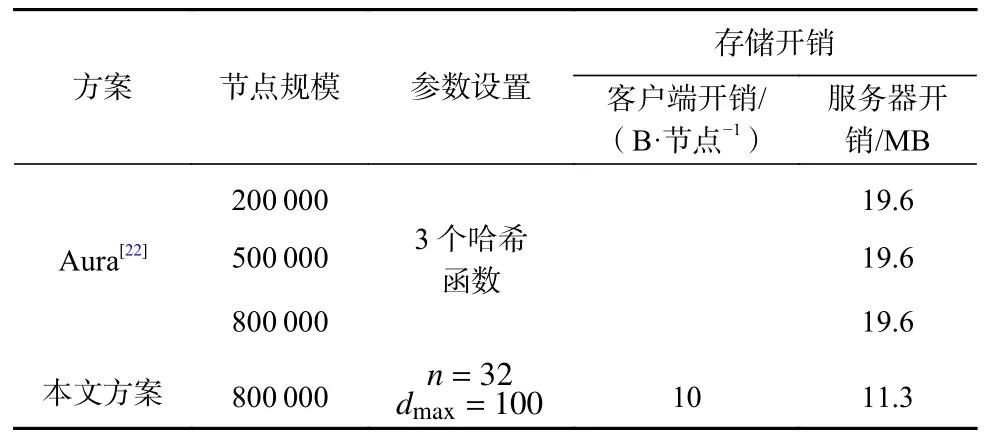
Table 4 Actual Storage Overhead of Schemes表4 方案實際存儲開銷

由于GGM 樹隨著節點規模的擴大，其計算時間迅速增加，如圖4 所示，本文方案通過增加節點使用列表，避免每次搜索時服務器需要生成全部穿刺密鑰，大大減少在匹配節點較少時搜索的響應時間，隨著匹配節點數的增多，方案平均搜索時間趨于一致.

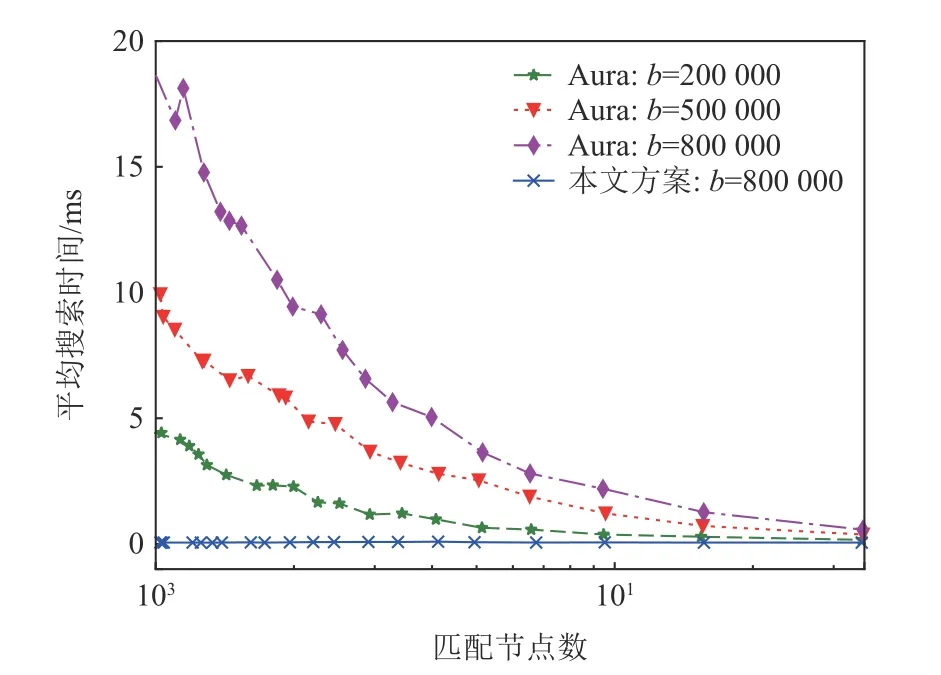
Fig.4 The comparison of actual search time（N = 100 000）圖4 實際搜索時間對比（N = 100 000）

如圖5 所示，在節點規模b=60 000時，客戶端運行查詢算法時向服務器發送的節點個數隨節點利用率 ρ的變化情況.在插入文檔索引較少時，發送數據隨文檔索引增加而增加，當 ρ ＞0.3時，發送的節點數逐漸提高.

圖6 為刪除索引后查詢到的匹配節點個數變化情況，可以看出本文方案不會發生誤刪除.圖7 為刪除索引時方案通信開銷變化情況.從圖7 可以看出，在頻繁發生索引刪除的DSSE 應用場景下，本文方案通信開銷也隨著刪除節點增多而逐漸降低.

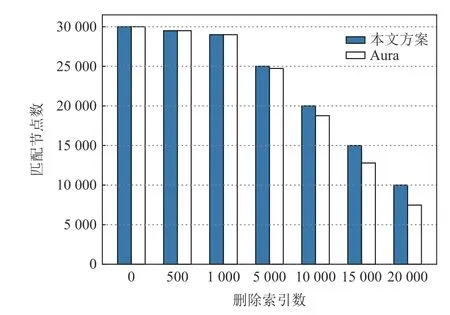
Fig.6 Search results after index deletion（b = 60 000, N =30 000）圖6 刪除索引后搜索結果（b = 60 000, N = 30 000）

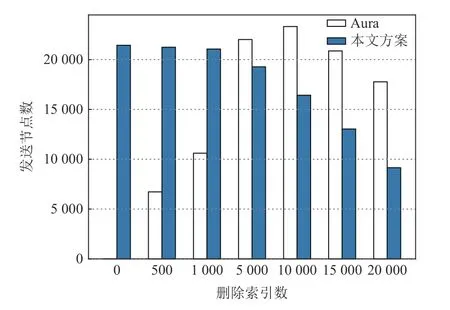
Fig.7 Scheme communication overhead comparison after index deletion（b = 60 000, N = 30 000）圖7 刪除索引后方案通信開銷對比（b = 60 000, N =30 000）

7 總 結

本文結合可搜索加密方案的應用場景，給出了動態對稱可搜索方案的形式化描述.同時給出了SRE 更嚴格的正確性定義，并通過理論分析證明了避免誤刪除發生的條件.在設計插入點位置選擇算法的基礎上，構造了基于SRE 的對稱可搜索加密方案.

大多數情況下，關鍵詞的使用密鑰節點數遠小于未使用節點數，通過為每個關鍵詞添加節點插入標志，記錄每個關鍵詞實際使用的節點位置信息，查詢時只發送已使用節點，可以大大降低服務器恢復密鑰時的時間開銷.理論分析和實現結果表明，本文方案進一步優化了Aura 方案搜索效率，有效避免了節點誤刪除問題.然而方案需要在客戶端存儲更多節點信息，增加了客戶端數據存儲開銷，同時在刪除索引較少的場景下，本文方案具有更大的通信開銷.下一步將在減少客戶端存儲開銷、方案通信開銷以及多客戶端場景下的擴展等問題上展開進一步研究.

作者貢獻聲明：黃一才提出了算法思路和實驗方案，并撰寫了論文；郁濱提出指導意見并修改論文；李森森參與了實驗方案制定及部分數據分析與整理.