基于FP-tree 和MapReduce 的集合相似度自連接算法

馮禹洪 吳坤漢 黃志鴻 馮洋洲 陳歡歡 白鑒聰 明 仲

1 （深圳大學計算機與軟件學院 廣東深圳 518060）

2 （中國科學技術大學計算機科學與技術學院 合肥 230027）（yuhongf@szu.edu.cn）

集合相似度自連接是大數據分析的重要操作，它是從一個集合集中找出相似度大于給定閾值的集合對，有著廣泛的應用，如協同過濾[1]、檢測近似重復的網頁[2]、社交網絡分析[3]等.其中，度量2 個集合的相似度可根據應用選擇合適的度量函數，如Jaccard函數.

集合相似度自連接需要度量集合集中所有集合對的相似度，時間復雜度為O(kn2)， 其中n為集合集的大小，k為任意2 個集合相似度的平均計算時間.當集合規模較大時，如2019 年第3 季度知名社交網絡平臺Facebook 的月活躍用戶人數為24.5 億[4]，每個用戶都有好友集合.Facebook 用戶好友集合的自連接計算中n=2.45×109，這樣的大規模數據集給時間復雜度高的集合相似度自連接計算帶來挑戰.基于要處理的數據是靜態數據還是動態數據（流數據），現有集合相似度自連接計算方法可以劃分為2 類：批處理式計算和流處理式計算.

首先，批處理式集合相似度自連接計算要處理的是靜態數據，運行過程中沒有新增數據.現有提高運行效率的批處理式集合相似度自連接計算方法可以劃分為2 類：近似計算方法和基于過濾-驗證框架的準確計算方法.近似計算方法通過設計合適的集合相似度快速估算方法來加速計算，如基于位置敏感哈希函數的MSJL[5]、基于局部敏感過濾的LSFJoin[6]、基于高維數據速寫和索引的CPSJoin[7]等，但因估算降低了精度導致不能找出所有相似度超過閾值的集合對.本文將關注準確計算方法.

基于過濾-驗證框架的準確計算方法包括allpair[8], PPJoin[2], MPJoin[9], AdaptJoin[10], GroupJoin[11]等，其計算采用先過濾后驗證的2 階段計算方法.第1 階段使用合適的過濾策略將檢測發現的相似度低于閾值的集合對刪除，獲得較小的候選集；第2 階段基于規模減小后的候選集驗證并輸出相似度大于給定閾值的集合對，提高了效率.有效的過濾策略是提高這類算法的重要支撐技術，常用策略包含長度過濾[12]、前綴過濾[8]、位置過濾[2]等.最近提出的位圖過濾[13]采用哈希函數創建表達集合特征為固定長度的位圖，然 后通過位操作推斷集合對相似的上界，實現相對使用其他策略最高達4.50 倍的性能提升.

同時，并行分布式計算方法通過將大規模計算或數據劃分為一系列較小的分片，每個分片被分發到不同計算節點上并行運行以提高計算效率.根據計算節點的體系結構，并行分布式集合相似度自連接計算可以劃分為基于GPU 的計算和基于CPU 的計算.基于GPU 的系列算法有效提升了集合相似度連接的計算性能[14]，但是，基于GPU 的實現需要對硬件有深入的了解，這往往需要編程者付出很高的學習成本.而基于CPU 的集群計算是更為普及的并行分布式計算，現有的基于CPU 的并行分布式集合相似度連接算法大部分基于MapReduce[15]框架.根據處理過程是否將集合切分為多段，基于MapReduce 框架和過濾-驗證框架的集合相似度連接算法可劃分為2 大類：1）集合整體過濾與驗證，這類算法包括RIDPairsPPJoin（下文簡稱為RP-PPJoin, 有些文獻也稱為VernicaJoin）[16]， MGJoin[17]，SSJ-2R[18]等；2）集合數據分段過濾與驗證，如FS-Join[19].第1 類算法將集合切分為多段，分段過濾，然后合并驗證.這類算法容易被理解，但存在同一集合多次重復驗證的現象.第2 算法避免了重復驗證.但當閾值較低時，這2 類算法產生的候選集規模都比較大，運行效率并不理想[20].

其次，流處理式集合相似度自連接計算處理的是動態數據，該數據指的是隨時間依次產生的數據，如網絡監控數據、氣象測控等.其數據量隨著時間增長，顯著特征是數據有時間戳，能快速生成.集合流處理計算通常基于批處理計算方法，引入集合相似度時間衰減因子、采樣降低數據量從而提高計算效率，如串行式計算的基于PPJoin 設計的流處理計算算法SSTR[21]、基于更新日志的遞增式流處理計算算法ALJoin[22]等，分布式計算的流處理計算算法BundleJoin[23]和KNN Join[24]等.

綜上所述，面向靜態數據基于MapReduce 的并行分布式集合相似度自連接計算效率無論對批處理式計算還是流處理式計算都很重要，本文擬采用頻繁模式樹（frequent pattern tree, FP-tree）[25]，通過用更緊湊的擴展前綴樹結構表示數據并壓縮到內存中處理，減小生成的候選集的規模，同時減少I/O 操作，降低后續計算復雜度.本文將系統地研究FP-tree 及其派生結構FP-tree*，設計針對集合相似度自連接計算更有效的FP-tree*，并設計相應的基于MapReduce 框架的并行分布式集合相似度自連接算法.本文的主要貢獻有3 點：

1）提出面向集合相似度自連接的遍歷效率更高的線性頻繁模式樹 TELP-tree（traversal efficient linear prefix tree）結構模型及基于它的集合相似度自連接算法TELP-SJ，該算法包括2 階段過濾算法，減小樹的規模和減少對樹結點的遍歷，降低集合對相似度計算和驗證的時空復雜度；

2）設計基于TELP-tree 和MapReduce 的并行分布式集合相似度自連接算法FastTELP-SJ；

3）基于4 組真實應用數據集進行3 組性能比較實驗，分別進行TELP-SJ 算法與其他基于FP-tree*的算 法，如FastTELP-SJ，TELP-SJ，FastTELP-SJ 等 和 現有其他基于 MapReduce 算法的比較，本文實驗結果展現了FastTELP-SJ 算法在處理高維大規模集合相似度自連接計算時的性能優于其他算法.

1 基于FP-tree 的集合相似度自連接算法

給定集合集x={x1,x2,…,xn} ， 任意xi,xj∈x，xi和xj都是集合，集合相似度度量函數sim(xi,xj) ，閾值t，x的集合相似度自連接是找出所有滿足sim(xi,xj)≥t的集合對 (xi,xj).

為方便討論，本文以Facebook 開放的大規模應用數據集Facebook applications dataset II[26]的部分數據為例，演示基于其構建的FP-tree 派生結構，面向集合相似度自連接計算存在的問題及后續算法的處理過程.示例數據如圖1 的X所示，其中uid代表用戶標識號，aid代表應用標識號.在示例數據的應用場景中，uid和aid可以分別被理解為集合標識號和元素標識號.對任一用戶ui，其使用的應用可表示為集合A(ui) ，如A(u1)={a1,a2,a3,a4,a5}.如式（1）所示，當集合A(ui)和A(uj)的 相 似 度sim(A(ui),A(uj))用Jaccard(A(ui),A(uj)) 來 計 算 時，sim(A(u1),A(u3))=3/(5+3-3)=0.6.

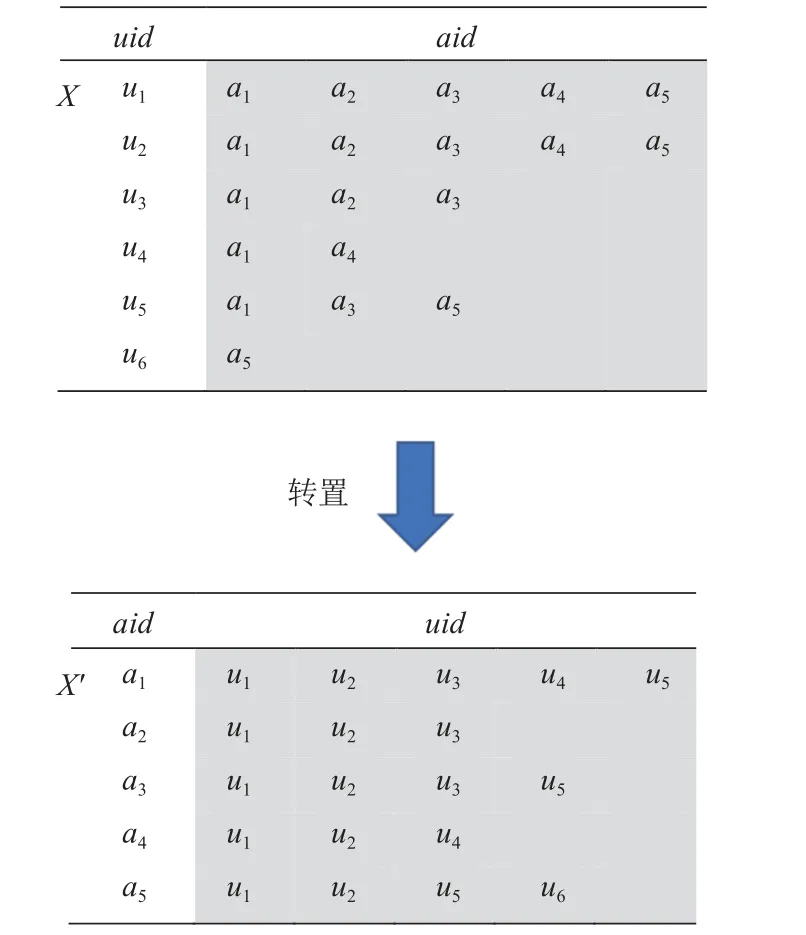
Fig.1 Transpose of sample data圖1 示例數據轉置

FP-tree 數據結構最初用于挖掘頻繁模式，為使用它來計算集合相似度自連接，我們首先要將其中集合交集大小的計算轉化為基于頻繁二項模式挖掘的計算.為此，轉置X的行與列得到X′的 數據，X中任意2 個集合A(ui)和A(uj)的 交集大小 |A(ui)∩A(uj)|的計算就轉換成X′中二項集 (ui,uj)出 現的頻次fi,j[27]的計算.如X′中 二項集 (u1,u3) 出現的頻次f1,3=3,示例數據中|A(u1)∩A(u3)|=|{a1,a2,a3}|=3，f1,3=|A(u1)∩A(u3)|.另外，X′中 一項集ui出 現的頻次與X中的 |A(ui)|出現的頻次也相等.

1.1 FP-tree 及其派生結構

FP-tree 是一種擴展前綴樹結構，該樹保留了所有項集的關聯信息，基于FP-tree 可以遞歸地挖掘出所有的頻繁項集[25].FP-tree 數據結構模型由2 部分組成：頭表和樹結構.頭表由三元組表示（元素，頻次，頭指針），其中“頭指針”指向樹結構中元素相同的第1 個結點，頭表中的三元組按照頻次遞減排序.樹結構結點由六元組表示（元素，頻次，計數，父結點指針，子結點指針，下一個元素相同結點的指針），其中“計數”指的是共同前綴出現頻次的計數，“下一個元素相同結點的指針”用于構建索引鏈，把樹中具有相同元素的結點鏈接起來.

構建FP-tree 包括構建頭表H和樹結構.X′中任一應用ai的 用戶集合標記為U(ai)，U(ai)元素按照頻次降序排序的序列標記為S(ai).首先初始化頭表和樹結構，將數據集中所有ui及 其一項頻次fi按照頻次倒序加入頭表中，相應頭指針L(ui)初始化為空指針，即索引鏈為空；而樹結構則初始化為元素為空的根結點.然后將X′中 任一應用ai相應的序列S(ai)插入頭表和樹結構中.對任一序列S(ai)，假設當前始于根且與S(ai) 有 最長共同前綴的路徑為P，則給共同前綴上所有結點的計數都加1，將S(ai)中不在共同前綴中的元素依序插入樹中，同時結點ui鏈接到對應元素的索引鏈的末尾.基于圖1 示例數據構建的FP-tree 見圖2（a）.為了簡化圖2 表示，樹結點信息僅展示其中的3 項，并以三元組格式展示（元素, 頻次, 計數）.

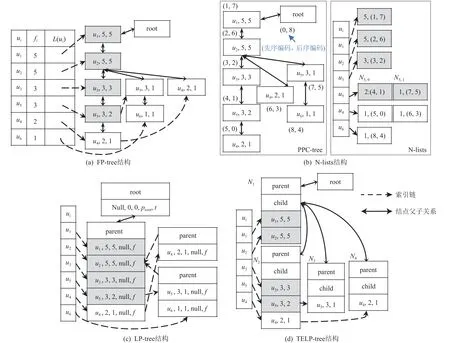
Fig.2 Construction of the FP-tree, N-lists, LP-tree, and TELP-tree over the sample data圖2 基于示例數據構建的FP-tree, N-lists, LP-tree, TELP-tree

構建好FP-tree 后，簡單的集合相似度自連接可以通過以下流程完成：首先根據頭表結點索引鏈遍歷樹并統計所有包含這些結點元素的二項集出現頻次，即相應集合交集大小；然后驗證2 個集合相似度是否大于閾值；最后輸出大于閾值的集合對.其中統計樹二項集的頻次時取二項計數值中較小者累加.例如，從頭表的u3開始，索引項的第1 個樹結點是(u3,3,3) ，沿分支向根結點方向遍歷并統計包含u3的二項集的頻次.其中 (u3,3,3;u1,5,5)的二項計數值較小者為3， (u3,3,3;u1,5,5)的 計算值為3，則f3,1暫時記為3.向上掃描完第1 個分支后，發現u3索引鏈只有1個 結 點，則f3,1=3.即 |A(u3)∩A(u1)|=3.而 |A(u3)|=3，|A(u1)|=5， 根據 式（1）得sim(A(u3),A(u1))=0.6，滿足閾值要求，輸出集合對 (u1,u3).而從u4開始，索引項的第1 個樹結點是 (u4,2,1)，沿分支向根結點方向遍歷得到 (u4,2,1;u1,5,5)的 計算值為1，則f4,1暫時記為1.向上掃描完第1 個分支后，沿著u4索引鏈找到FP-tree的下一個結點 (u4,2,1) ，同理得到 (u4,2,1;u1,5,5)的計算 值為1，則f4,1=f4,1+1=2 ， 即 |A(u4)∩A(u1)|=2.而A(u4)=2，A(u1)=5， 根 據 式（1）得sim(A(u4),A(u1))=0.4 ＜0.6 ，不輸出集合對 (u1,u4).

由于基于FP-tree 的多項集頻次計算或頻繁多項集挖掘需要遞歸建樹，運行期開銷大.為減少這一開銷，N-lists[28]采用垂直數據結構表示FP-tree 樹結點，FP-tree 樹結點的構建過程包含2 步：1）構建一種類似FP-tree 的樹結構-前序后序編碼樹（pre-order postorder code tree, PPC-tree）；2）構建PPC-tree 結點列表Nlist.如圖2（b）所示，PPC-tree 基本與FP-tree 結構相似，不同之處在于PPC-tree 不包含索引鏈，同時每個樹結點增加了標識結點在先序樹遍歷和后序樹遍歷中位置的先序編碼和后序編碼.PPC-tree 結點旁邊括號中的數字，左邊是先序編碼，右邊是后序編碼.結合2個結點的先序編碼、后序編碼可快速判斷2 個結點之間的祖先后代關系：祖先結點的先序編碼大且后序編碼小.為此，PPC-tree 的建樹過程增加了2 次樹的遍歷：先序遍歷和后序遍歷.N-lists 是由PPC-tree中元素相同的結點按先序編碼升序排序的列表，其數據結構包含頭表和元素的結點列表N-list.頭表結構及內容與圖2（a）類似，只是頭指針指向相應元素的N-list 首地址.本文的圖2（b）中只畫出頭表中的元素信息部分.N-lists 的結點數據結構為三元組：（計數，（先序編碼，后序編碼））.頭表元素ui的N-list 的第1個結點表項記為Ni,0， 第2 個結點表項記為Ni,1，依此類推.如u5的 第1 個結點N5,0=(2,(4,1)).特別地，頭表元素的N-list 各項計數之和為元素的單項頻次，例如，u5的 N-list 中2 項元組的計數之和為N5,0.計數+N5,1.計數=2+1=3=f5.

假定二項集 (ui,uj)都 是排序的二項集，ui的先序編碼小于uj，則 (ui,uj)的N-list 也是按先序編碼升序排序的列表，可通過將ui與uj的N-lists 按規則相交合并而成：分別取ui和uj的 N-lists 上的任意一個結點Ni,k和Nj,l,如果結點之間存在祖先后代關系，則將(Nj,l.計數,(Ni,k.先序編碼,Ni,k.后序編碼)) 插 入 (ui,uj)的N-list 中.例如，u3和u5對應的N-lists 相交合并可生成(u3,u5) 的N-list， 首 先u3的N-list 只 包 含1 個 結 點N3,0=(3,(3,2))，u5的 N-list 包含2 個三元組N5,0=(2,(4,1)),N5,1=(1,(7,5)).當 比 較N3,0和N5,0時 ，由 于 3 ＜4且2 ＞1，N3,0是N5,0的祖先，即它們間有祖先后代關系，則向 (u3,u5) 的N-list 中插入1 個結點N(3,5),0=(N5,0.計數,(N3,0.先序編碼,N3,0.后序編碼))=(2,(3,2))； 當 比 較N3,0和N5,1時 ，由于 3 ＜7且 2 ＜5，它們之間沒有祖先后代關系，因此不必向 (u3,u5)的N-list 插入新的結點.同理，頻次fi,j的計算可以通過對 (ui,uj)的N-list 各項計數求和得到，如f3,5=2， 即 |A(u3)∩A(u5)|=2， 而 |A(u3)|=3，|A(u5)|=3， 根 據 式（1）得sim(A(u3),A(u5))=0.5，不 滿足閾值要求，不輸出集合對 (u3,u5).

基于N-lists 的多項集頻次計算是基于N-lists 進行交叉合并的，不需要遞歸建樹，提升了計算性能，但在只計算二項頻次時轉變為2 個N-lists 的所有元素兩兩對比的計算，性能反而不理想.而面向大規模集合構建的FP-tree 的樹結點數量多，指針結點的尋址時間長，緩存訪問命中率低，降低了遍歷樹的效率.線性前綴樹（linear prefix tree, LP-tree）[29]，在FP-tree 結構的基礎上將其結點的元素字段改用數組表示，存儲多個元素信息，減少內存使用并加快尋址.如圖2（c）所示，LP-tree 的頭表結構及內容與圖2 （a）完全一樣，所以本文只畫出頭表中的元素信息部分.而結點信息改為2 項內容：一個是存儲元素信息的數組，另一個是父結點.該數組每一項的數據域用五元組表示（元素, 頻次, 計數, 下一個元素相同結點的指針, 分支標志）.其中，“下一個元素相同結點的指針”用于構建索引鏈，指向下一個元素相同的項在另一個結點的數組中的位置.父結點指向其前綴最后一個元素所在的結點及其在數組的位置.其中，當一個元素沒有下一個元素相同的結點時，相應指針為 N ull.分支標志為t時表示有大于等于2 個以上的序列片段的最長共同前綴止于該元素，f表示不存在分支.LPtree 結點結構合并了多個元素結點的信息，減少了FPtree 樹結點數量，圖2（a）中的FP-tree 有9 個結點，而圖2（c）中的LP-tree 只有4 個結點.LP-tree 通過連續存儲元素信息提高了計算的效率，但結點內部存在的分支、復雜的遍歷流程帶來運行期開銷.

1.2 TELP-tree 數據結構

為進一步提高基于FP-tree*的集合相似度自連接的計算效率，我們提出了一種遍歷效率更高的線性前綴樹TELP-tree（traversal efficient LP-tree）的數據結構.與線性前綴樹LP-tree 相似，TELP-tree 的樹結點也采用線性數組存儲多個元素信息以減少樹結點數量，提高樹的遍歷效率；而不同的是，TELP-tree 樹結點內部沒有分支，避免結點內分支帶來復雜的運行期遍歷流程管理，從而減少相應的運行期開銷.

定義1.TELP-tree.TELP-tree，數據結構包含頭表H和樹結構，頭表H與FP-tree 一樣結構.TELP-tree 樹結點（TELP-tree node）N包含建樹和遍歷樹所需的3項內容：父結點P、子結點C和存儲元素信息的數組E，即一個包含k個元素的Ni表示為Ni={P,C,E={E1,E2,…,Ek}}.而數組元素Ej可用三元組（元素, 頻次, 計數）表示.一個由c個樹結點組成的TELP-tree 可以表示為 {H,N1,N2,…,Nc}.

TELP-tree 的頭表與FP-tree 一樣，因此，構建TELP-tree 頭表與構建FP-tree 的方式是一樣的.而樹結點間存在差異，因此TELP-tree 樹結構的構建與FPtree, LP-tree 的構建也存在差別.對任一序列S(ai)，與FP-tree, LP-tree 相似，始于根結點，找到TELP-tree 中與S(ai) 有 最長共同前綴的路徑P，將P相應共同前綴上結點中所有元素的計數加1，然后將這些元素從S(ai)中移去，形成S(ai)′.如果||S(ai)′||=0，對該序列的處理完成.否則，設P上最后1 個結點中與S(ai)′有最長公共前綴的后繼結點為Nsucc，根據該公共前綴長度是否為0，樹結點的構建和樹結點插入到樹結構有所不同：1）長度為0 時，構建一個新的結點，將S(ai)′中的元素依序存進其數組中，并將該結點插入樹結構和鏈接到對應元素的索引鏈的末尾，這種情況與LPtree 的樹結構構建是一致的；2）長度不為0 時，將Nsucc所有公共前綴上的元素計數加1.然后將S(ai)′中在 公 共前 綴 上 的 元 素 移 除， 形 成S(ai)′′,如 果||S(ai)′′||=0，對該序列的處理完成，這種情況與LPtree 的樹結構構建是一致的.如果||S(ai)′′||=0，將構建一個新的結點N′， 將S(ai)′′中的元素都依序存進其數組中.同時將Nsucc中不是公共前綴的元素都移出，重構一個新的結點N′′.最后將新構建的結點N′和N′′插入樹中，即Nsucc是N′和N′′的父結點，并將N'和N''分別鏈接到對應元素的索引鏈的末尾.這一步是TELPtree 與LP-tree 因為樹結點結構不同帶來的樹結構構建的不同之處，結點內部沒有分支，簡化了樹結點的同時也簡化了樹結構的構建.

基于圖1 數據構建的TELP-tree 如圖2（d）所示，其中 (u1,5;u2,5)是所有輸入序列的公共前綴，基于構建 樹 的 規 則， (u1,5)和 (u2,5)將 分 別 成 為TELP-tree 的1 個結點里的2 個數組元素.而序列(u1,5;u2,5;u3,3;u5,3;u4,2)移 去公共前綴 (u1,5;u2,5)之后的后續片段為(u3,3;u5,3;u4,2)，(u1,5;u2,5;u3,3;u5,3)移 除 公 共 前 綴(u1,5;u2,5) 后是 (u3,3;u5,3)， (u1,5;u2,5;u3,3)移除公共前 綴 (u1,5;u2,5) 后 是 (u3,3)， (u3,3;u5,3)是(u3,3;u5,3;u4,2)的子序列，而(u5,3)和(u4,2)沒有公共前綴，所以(u1,5), (u2,5), (u3,3)這3 個數組元素組成1 個結點，計數值分別是3, 2, 1，且結點內部沒有分支.最終構建的TELP-tree 有5 個結點.

相 比圖2（a）中9 個 結 點 的FP-tree，圖2（d）中5個結點的TELP-tree 結點少4 個，結點內數組元素尋址快.相比圖2（c）的4 個結點的LP-tree，TELP-tree 的結點多了1 個，但結點數組中存儲的信息少，且前綴所在結點直接指向后續片段所在結點，避免了結點內部分支，簡化并加速樹的遍歷.

1.3 TELP-SJ 算法

1.1 節描述了簡單的基于FP-tree*的集合相似度自連接計算流程，但該計算過程沒有采用過濾-驗證框架.為進一步提高基于FP-tree*的集合相似度自連接計算效率，本節設計基于過濾-驗證框架和TELPtree 的集合相似度自連接算法TELP-SJ.

TELP-SJ 使用長度過濾策略來設計其過濾算法.長度過濾策略被應用于多個集合相似度自連接算法中，如FS-Join.當集合相似度函數為Jaccard（）時，長度過濾策略如定理1[19]所示.

定理1.給定2 個集合A和B,|A|＜|B|， 閾值t，如果|A|＜t×|B|， 那么sim(A,B)＜t.

文獻[19]給出定理1 的數學證明，基于定理1，2個相似的集合應有相似的大小，反之，集合大小不相似的集合對的相似度低.與集合A的相似度大于等于t的所有集合，其集合大小一定小于等于 |A|/t.因此，可提前過濾集合大小大于 |A|/t的集合.根據1.1 節和1.2 節的建樹過程可知，序列的長度將影響樹的深度，長度越大，深度越深，樹的遍歷代價就越高.為減小構建的樹的規模，根據定理1，我們首先設計面向構建樹的過濾算法，該算法檢測、發現并刪除序列中不會與其他集合形成相似度高于閾值的集合對的集合.給定至少有2 個元組的序列S(ai)，在將它插入到TELP-tree 時前先應用算法1 描述的面向構建樹的過濾算法對其進行預處理：從右向左掃描S(ai)中的元素，假設最右邊的2 個相鄰元素分別是uk和uj,如果|A(uk)|＞t×|A(uj)|， 將S(ai)按照2.2 節描述的建樹過程插入TELP-tree.如果 |A(uk)|＜t×|A(uj)|，根據定理1，我們有sim(A(uk),A(uj))＜t，即uk與uj的相似度低于閾值t.序列片段按元素頻次降序排列，此時，uk對應的元組 (uk,A(uk)) 將 從序列S(ai)中刪除.刪除后如果|S(ai)|≤ 1，意味著ai對應原序列中所有元素相似度都低于閾值t，原序列被舍棄，否則繼續如上述過程迭代處理S(ai).面向構建樹的過濾算法如算法1 所示.函數getrightmost(S(ai))表 示獲取S(ai)的最右邊元素.

算法1.面向構建樹的過濾算法.

輸入：序列S(ai)；

輸出：過濾后序列S′(ai).

①S′(ai)←S(ai)；

② while |S′(ai)|＞1 do

③ (uk,A(uk))←getrightmost(S′(ai))；

④S′′(ai)←S′(ai)-(uk,A(uk))；

⑤ (uj,A(uj))←getrightmost(S′′(ai))；

⑥ if |A(uk)|≥t×||A(uj)||

⑦ break；

⑧ else

⑨S′(ai)←S′′(ai)；

⑩ end if

? end while

? returnS′(ai).

例如，針對圖1 的示例數據，S(a5)=(u1,5;u2,5;u5,3;u6,1)， 從右向左掃描S(a5)， 最右邊的 |A(u6)|=1，而過濾算法根據構建樹（算法1），構建樹的過程就是逐步插入樹節點的過程 |A(u5)|=3， 1/3 ＜0.6，根據面向構建樹的過濾算法刪除元組 (u6,1)， 得到S′(a5)=(u1,5;u2,5;u5,3).此時最右邊的|A(u5)|=3， 而|A(u2)|=5，3/5=0.6 ，將S′(a5)插入到 TELP-tree.應用面向構建樹的過濾算法構建的TELP-tree 如圖3 所示，與圖2（d）中沒有應用該過濾算法構建的TELP-tree 相比，圖3中的TELP-tree 減少了1 個樹結點N4， 樹的結點N3的數組元素減少了1 個，頭表元素 |H|也減少了1 個，即少了u6相應的信息.

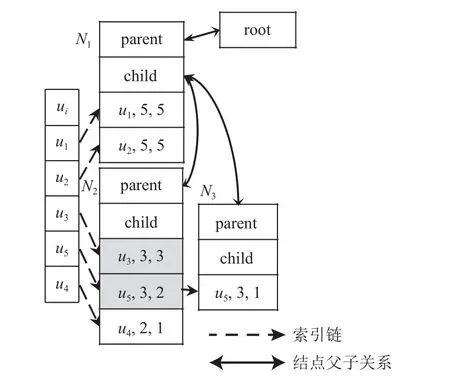
Fig.3 A TELP-tree is constructed based on filtering algorithm圖3 基于過濾算法構建的TELP-tree

構建好TELP-tree 后，通過沿著頭表結點索引鏈遍歷樹并統計所有以這些結點為后綴的二項集頻次，根據樹的特征，樹結點元素頻次越高越靠近根結點.樹結點內數組元素按頻次倒序排序.樹的遍歷代價跟遍歷的結點數和結點內數據元素的個數有關.沿著索引鏈從遠離根結點的樹結點向著根結點的方向遍歷樹，統計索引鏈結點元素與其他元素的二項頻次.同樣，根據定理1，非根結點元素ui及其祖先結點元 素uj如 果 滿 足 |A(ui)|＜t×|A(uj)|， 可 得sim(A(ui),A(uj))＜t，即這2 個元素相似度低于閾值，此時，可以停止沿著這條分支向著根結點方向統計，即過濾對應的集合對以減少遍歷.面向遍歷樹的過濾算法見算法2，其中，Ancestor(N)表 示樹中N的祖先結點；N.x中 的“.” 表示 取結點N的 相應數 據域x， 如N.E[l]表示取結點N的元素數組E的第l個元素.

算法2.面向遍歷樹的過濾算法.

輸入：元素ui, 樹結點N, 頻次統計f；

輸出：頻次統計f.

① whileN不為根結點 do

②l←|N.E|-1；

③ whilel≥0 do

④ if|A(ui)|＜t×|A(N.E[l])|

⑤ goto ?；

⑥ else

⑦fi,N.E[l]+=N.E[l].計數

⑧ endif

⑨ end while

⑩N←Ancestor(N)；

? end while

? returnf.

基于面向構建樹的過濾算法構建TELP-tree，按規則遍歷樹并計算集合相似度自連接：1）遍歷頭表H中所有元素ui， 并初始化f；2）通過ui的索引鏈，遍歷其所有樹結點，對每個樹結點調用面向遍歷樹的過濾算法，并更新f；3）根據f計算出集合相似性，并輸出相似性大于閾值的集合對.例如從圖3 的頭表的(u4,2)開 始，順著索引項第1 個樹結點N2的數組元素(u4,2,1) 開始統計包含u4的二項集的頻次.如(u4,2,1;u5,3,2)的 二項計數值較小者為1，則f4,5=0+1=1.同時注意到 |A(u4)|=2， |A(u2)|=5， 2 ＜0.6×5，因此，針對 (u4,2,1) ，從N2向著根結點的方向遍歷樹時，只需要遍歷N2的 元素信息數組，不需要遍歷N1.因此f4,5=1， 即|A(u4)∩A(u5)|=1.而|A(u4)|=2，|A(u5)|=3，根據式（1）得sim(A(u4),A(u5))=0.25 ＜0.6，不輸出集合對 (u4,u5).圖2 和圖3 中灰色框的元素表示統計包含u4的二項集頻次時要遍歷的元素，沒有填充灰色的框的結點和數組元素表示沒有遍歷的點或元素.由此，針對TELP-tree，統計包含u4的二項集的頻次要遍歷的結點數和數組元素分別是1 和2，而在使用過濾算法的情況下，要遍歷的結點數和數組元素的分別是3 和6，遍歷次數大大減少，提高了遍歷效率.

以上面向構建樹和樹遍歷的2 個過濾算法同樣可以使用于其他基于FP-tree*的集合相似度自連接算法.綜上，TELP-SJ 的算法的偽代碼見算法3.基于FP-tree 的集合相似度自連接算法FP-SJ、基于LP-tree的 LP-SJ 均與 TELP-SJ 的計算思路基本一致，不同之處在于算法3 中行?，即：如果是FP-SJ，則構建FPtree；如果是LP-SJ，則構建LP-tree.遍歷樹的一些細節有稍許區別，如Ancestor(nk)的實現和結點的定位等操作，這里不贅述.而基于N-lists 的集合相似度自連接算法PPC-SJ，則是構建PPC-tree 后，構造N-lists，然后對任意2 個N-lists 的所有元素兩兩對比驗證完成 計 算.FP-SJ，LP-SJ， TELP-SJ，PPC-SJ 這4 種 基 于FP-tree*的集合相似度自連接算法統稱為FP-tree*-SJ.

算法3.TELP-SJ 算法.

輸入：數據集D={〈ui,{ai1,ai2,…,aik}〉} ， 閾值t；

輸出：滿足閾值的集合對集合P.

①U←?，S←?，S′←?，P←?；

② for eachui，A(ui)inD

③ for eachaij∈A(ui)

④U(ai j)←U(aij)+(ui:|A(ui)|)；

⑤ end for

⑥ end for

⑦ forU(ai) inU

⑧ 對U(ai)按 頻次降序排序得到S(ai)；

⑨ 對S(ai) 調 用算法1 得到S′(ai)；

⑩ end for

? 根據S′建樹tree；

? for eachui∈tree.H

? 初始化頻次f；

? for eachNkinui的索引鏈

? 對ui，Nk，f調用算法2；

? end for

? 根據f計算出sim(ui,uj)；

?P←P+{(ui,uj)s.t.sim(ui,uj)＞t}；

? end for

? returnP.

2 基于MapReduce 的集合相似度自連接算法FastTELP-SJ

MapReduce 是一種高效的并行分布式集群計算框架.一個MapReduce 任務的運行主要包含2 個階段：映射（Map）階段和規約（Reduce）階段.Map 階段首先將存儲在分布式文件系統HDFS 上的輸入數據劃分為多個分片；然后就近分發至集群多個計算節點獨立并行運行函數map，處理數據并以〈Key,Value〉對的形式輸出中間結果.之后中間結果按照Key值進行合并（combine）、重新分配（shuffle）、排序（sort）后再分發至1 個或多個節點進行Reduce 階段運算，獨立并行運行函數reduce進行匯總.最終各個函數reduce的結果仍以〈Key,Value〉對的方式輸出并保存在HDFS 上.

第1 節設計了系列基于FP-tree 及其擴展結構的集合相似度自連接算法FP-tree*-SJ，這些算法的特征是建樹后，整棵樹需要保留在內存中進行計算，當集合規模增大時，樹的規模增大，對內存的要求增大，樹的遍歷計算代價也增大.為進一步提高計算性能，本節設計基于TELP-tree 和MapReduce 的集合相似度自連接算法FastTELP-SJ.圖4 展示了FastTELP-SJ 的計算過程.FastTELP-SJ 包含2 個MapReduce 任務，分別完成數據集轉置、建樹和集合相似度自連接的計算.1.3 節設計的2 階段過濾算法，分別應用于任務1和任務2.

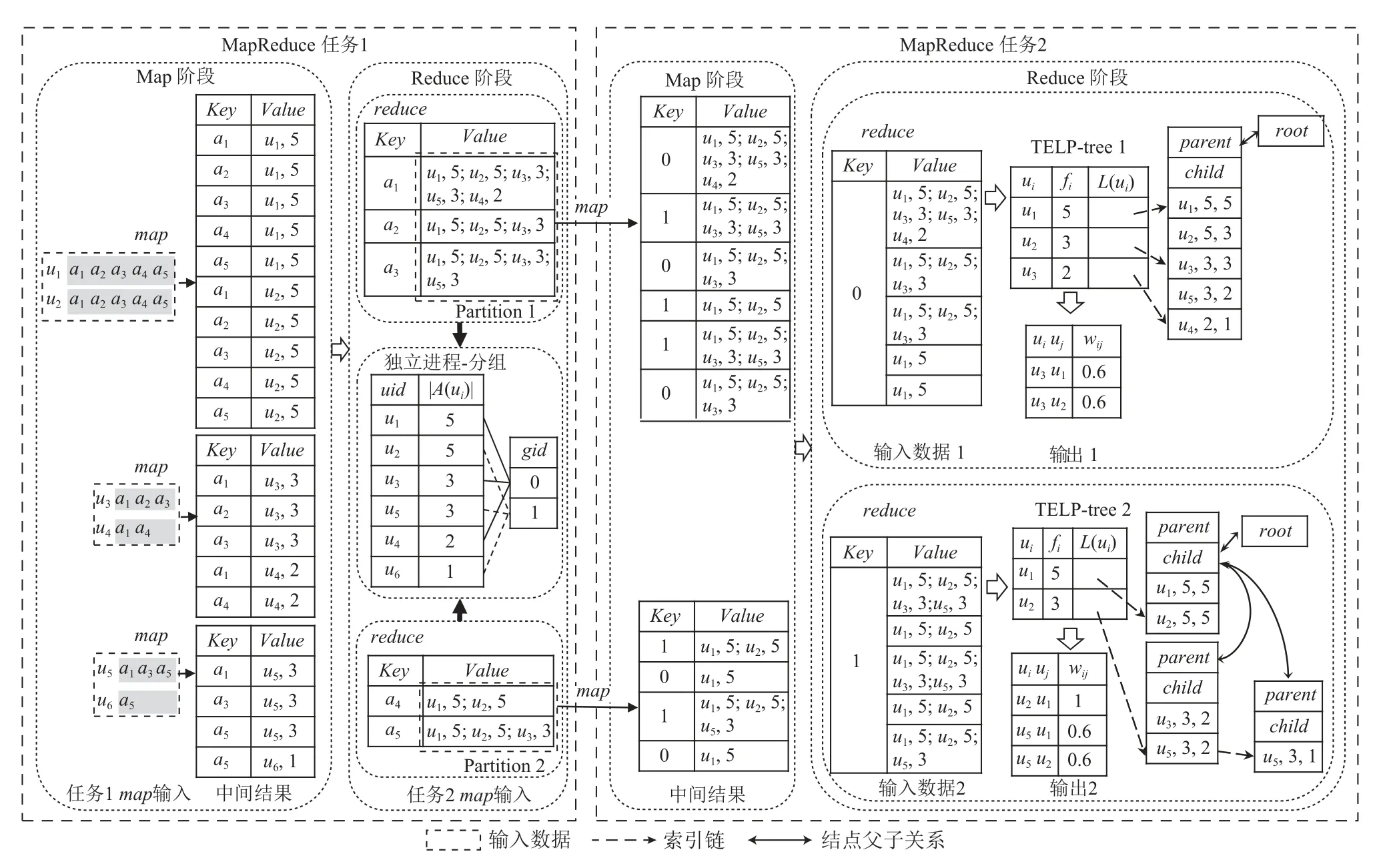
Fig.4 An illustration of the computation process of the parallel and distributed set similarity self-join of FastTELP-SJ with MapReduce圖4 基于MapReduce 的并行分布式集合相似度自連接FastTELP-SJ 的計算流程示意圖

2.1 轉置數據集

任務1 的函數map計算每個ui的 頻次 |A(ui)|、輸出〈Key=aid,Value=(ui:|A(ui)|)〉對, 實現了原數據集的轉置.與Key值 相同的Value將被合并和發送到同一個函數reduce.任一應用ai的Value集合標記為U(ai).函數reduce 將U(ai)元素按照頻次降序排序得到序列S(ai)， 調用算法1 得到S′(ai)， 輸出鍵值對〈Key=ai,Value=S′(ai)〉.例如，圖4 任務1 的Reduce 階段中S(a5)=(u1,5;u2,5;u5,3;u6,1) , 函數reduce對S(a5)應用算法1，從右向左掃描S(a5)， 最右邊的 |A(u6)|=1， 而 |A(u5)|=3，1/3 ＜0.6 ，刪 除 數 據 (u6,1).同 時 |A(u2)|=5， 3/5 ≥0.6，因此輸出結果〈a5,(u1,5;u2,5;u5,3)〉.任務1 的函數map與reduce的功能分別與算法3 中行②～⑥和行⑦～⑩類似，故不再贅述.

當所有reduce函數完成計算后，節點master將啟動一個獨立進程對元素分組，按照頻次將元素排序，函數seq(ui)表 示ui的序號.假設gNum表 示組數，gi表示ui的組標識號gid.基于FP-tree 樹的并行分布式計算有多種分組策略[30]，這里采用基于均衡預估遍歷負載的策略，即gi=seq(ui)modgNum.

2.2 構建樹并計算集合相似度自連接

FastTELP-SJ 采用集合數據分段過濾與驗證的設計思路，為此，任務2 首先切分序列，按分段劃分數據集，然后根據數據集分片并行獨立構建TELP-tree計算集合相似度自連接.其中函數map完成數據集劃分工作.對任一S(ai)，函數map的工作流程為：1）根據S(ai) 最 右邊元素gid輸出鍵值對〈Key=gid,Value=S(ai)〉 ；2）從右向左遍歷S(ai)中 的元素uk， 如果與gid即gk相 等的鍵值對已輸出，則將該uk從S(ai)中刪去；如果S(ai)不為空，跳回1）繼續迭代執行.例如，圖4任務2 的函數map對序列S(a5)=(u1,5;u2,5;u5,3)將輸出2 個結果：〈 1,(u1,5;u2,5)〉 和〈0,(u1,5;u2,5;u5,3)〉.任務2 中切分序列的偽代碼如算法4 所示.

算法4.序列切分算法.

輸入：已排序序列S(ai) ， 元素分組gid；

輸出：劃分結果R=〈{gid,S〉}.

①R←?,G←?；

② while|S(ai)|＞0

③(uik,|A(uik)|)←getrightmost(S(ai))；

④ifgik∈G

⑤R←R∪{〈gik,S(ai)〉}；

⑥G←G∪{gik}；

⑦ end if

⑧S(ai)←S(ai)-(uik,|A(uik)|)；

⑨ end while

⑩ returnR.

所有Key即gid相同的序列片段將被分配給同一個節點的函數reduce.因為集合相似度自連接僅需要計算單項頻次和二項頻次，結合面向MapReduce 計算而設計的精簡FP-tree（reduced FP-tree）[29]的結構特征，函數reduce在構建TELP-tree 時，僅為gid與Key值相同的元素構建頭表和索引鏈，減少內存空間并減少建樹時間，相應的TELP-tree 稱為精簡TELP-tree.除此之外，樹的構建過程與1.2 節相同.

構建好精簡TELP-tree 后，通過對頭表結點索引鏈應用面向遍歷樹的過濾規則遍歷樹，并統計所有以這些結點為后綴的二項集出現頻次.其中樹遍歷過程與1.3 節描述的相同，而二項集頻次統計僅對gid與reduce的Key值相同的結點進行統計.任務2 的函數reduce與算法4 的行?～?類似，故不再贅述.

綜上，FastTELP-SJ 算法的計算流程示例見圖4.其他FP-tree*-SJ 的MapReduce 計算可采用類似的設計，相應地，基于MapReduce 的FP-tree*-SJ 算法被命名為FastFP-tree*-SJ.

3 性能評估

基于FP-tree*的算法通過將數據壓縮在內存中進行計算，減少I/O 操作，減小候選集，提高驗證兩兩集合相似度是否大于閾值的運行效率.但這些算法也增加了動態構建樹等運行期開銷，同時，整棵樹需被保留在內存中進行計算，對內存需求比較大.我們將從運行時間、內存占用率、磁盤使用量這3 類指標通過3 組比較實驗評估FastTELP-SJ 算法的性能：1）TELP-SJ 算法與基于其他FP-tree*-SJ 算法的比較；2）FastTELP-SJ 算法與TELP-SJ 算法的比較；3）FastTELPSJ 與現有經典算法的比較.

Apache Hadoop[31]和 Apache Spark[32]是2 個最知名和最廣泛使用的MapReduce 編程模型的開源實現.兩者最大的區別是：Apache Hadoop 的中間計算結果保存在Apache Hadoop 分布式文件系統中，而Apache Spark 可將中間數據結果緩存在內存中.因此，對多次數據依賴的迭代算法、多數據依賴的計算任務，使用Apache Spark 可以減少I/O 從而提高運行效率.從第2 節的描述可見，集合相似度自連接計算不包含多次數據依賴的迭代計算.另外，還有些特定面向多核或眾核優化的MapReduce 實現，如Phoenix[33], Mars[34]等.考慮到現有經典算法都是基于Apache Hadoop 實現，因此，本文的對比實驗首先在Apache Hadoop 上復現經典算法，然后實現本文設計的算法.

實驗使用一個包含17 個曙光TC4600 刀片節點搭建的Apache Hadoop 集群，其中1 個作為主節點，其他作為從節點.每個刀片都有2 個10 核的Intel?Xeon?E5-2 680 v2 2.8 GHz 的處理器、2 個1 TB 的磁盤、64 GB 的內存和1 Gbps 的以太網.刀片上安裝CentOS 6.5 操 作 系 統， OpenJDK 1.8.0 和 Apache Hadoop 2.7.1.相關Apache Hadoop 參數配置見表1，其他均采用缺省配置.

Table 1 Apache Hadoop Parameter Configuration表1 Apache Hadoop 參數配置

實驗數據來自4 組真實的應用數據集：Facebook應用數據集 II（簡記為facebook）[35]、匈牙利在線新聞門戶點擊流數據集kosarak[36]、2015 年Enron 電子郵件數據集Enron[37]和交通事故數據集accidents[38].我們將從各組數據集中提取一定量的數據分別進行實驗，相應數據子集命名為數據集名稱后加提取的數量，如從facebook 數據集中提取10 萬條數據，記為facebook10w.4 組數據集為各取近30 萬條數據組成的子集，其相應數據特征總結在表2 中，其中，子集x′={x′1,x′2,…,x′n′}， 子集大小即 |x′|=n′為數據子集元素總數，表示數據集所有元素屬性合集，X(a′i)表 示擁有屬性a′i的元素，表示擁有該屬性的元素的最大個數表示所有屬性元素的平均個數，表示元素擁有屬性的最大個數，表示元素擁有屬性的平均個數，表示元素擁有屬性個數的方差.每次計算都將運行3 次，采用平均運行時間、內存占用率峰值和磁盤使用量用于展示實驗結果和分析.

Table 2 Characteristics of Experimental Datasets表2 實驗數據集特征

3.1 TELP-SJ 與基于其他FP-tree＊-SJ 的比較

本文分別實現FP-SJ, PPC-SJ, LP-SJ, TELP-SJ 這4 種基于 FP-tree 及其派生結構的集合相似度自連接算法，并將這些算法分別運行在facebook30w,kosarak30w, Enron30w, accidents30w 這4 組數據上，閾值t的取值范圍為 0.6 ～0.9.基于FP-tree*-SJ 的集合相似度自連接計算沒有產生中間結果，最后輸出結果是一樣的，因此這4 種算法的磁盤使用量沒有差異.這4 組算法的區別在于樹結構的差異及因此帶來的建樹和遍歷樹流程的差異，我們將比較這4 種算法的運行時間和內存占用率峰值.

1） 運行時間

根據第1 節的描述，基于FP-tree*的集合相似度計算的第1 步是轉置數據集.數據子集x′轉置后的數據 集x′′的 大 小 |x′′|為x′所 有 元 素 屬 性 合 集 大 小 |A(x′)|，即|x′′|=|A(x′)|.FP-SJ, LP-SJ, TELP-SJ 等算法的計算復雜度即樹遍歷的復雜度而對PPC-SJ來說，基于構建好N-lists的集合相似度自連接計算是對任意2個N-lists的比較，其計算復雜度O(Nlists)=|x′|×|A(x′)|2.

圖5 展示4 種FP-tree*-SJ 算法的運行時間隨著閾值t提高的變化，我們可以看到在facebook30w,Enron30w, kosarak30w 這3 組數據集上FP-SJ, LP-SJ,TELP-SJ 的運行時間比PPC-SJ 的運行時間少很多.如表2 所示，這3 組數據的 |A(x′)|很大，說明原數據子集元素屬性合集很大，即是高維大數據.該實驗數據說明這3 種算法比PPC-SJ 更適合處理高維大規模集合相似度自連接計算，其中TELP-SJ 的運行時間最少.

Fig.5 Relationship between FP-tree*-SJ’s running time and the threshold圖5 FP-tree*-SJ 的運行時間與閾值關系

在accidents30w 數據集上PPC-SJ 的運行效率最好，其次是TELP-SJ, 最差是FP-SJ.accidents30w 的|A(x′)|=458， 而其 他3 組的都很大，所以PPC-SJ 的運行效率最好.該實驗數據說明PPC-SJ 比其他3 種算法適合處理低維大規模集合相似度自連接計算.此種情況下，TELP-SJ 比FP-SJ, LP-SJ 的運行效率也要高.

表3 展示了閾值t= 0.6 時4 種FP-tree*-SJ 算法處理Enron30w 數據集時各分步的運行時間，包括建樹時間、遍歷樹時間、總耗時.表4 展示了TELP- SJ與其他3 種算法的相對性能提升率.由表3 和表4 可見，4 種算法遍歷樹的時間在總耗時中占比較高，而TELP-SJ 和LP-SJ 的遍歷時間少于FP-SJ 和PPC-SJ，這與第1 節的分析一致.其中，TELP-SJ 的遍歷時間最少，相比于FP-SJ 和PPC-SJ 性能分別提高了32%和83%.同時，我們也看到，TELP-SJ 的建樹時間和遍歷樹時間都比LP-SJ 少，其中建樹時間性能提高了45%，遍歷時間性能提高了17%，這也與第1 節的分析一致.隨著閾值t的增大，因為大部分數據在第1階段過濾中被過濾掉，候選集規模小，建樹和遍歷樹的代價差異減小，相應地TELP-SJ 與FP-SJ 和 LP-SJ的運行時間差異減小.

Table 3 Detailed Execution Time of Enron30w Dataset handled by FP-tree＊-SJ表3 FP-tree＊-SJ處理Enron30w數據集的細分運行時間 s

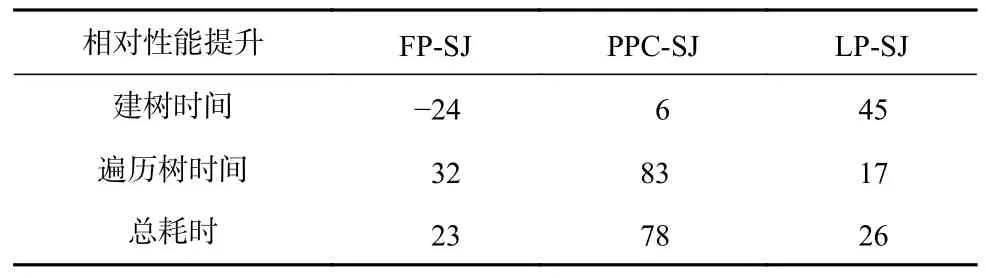
Table 4 Relative Performance Improvement of TELP-SJ Compared with Other FP-tree＊-SJ表4 TELP-SJ 相對于其他FP-tree＊-SJ 的性能提升 %

我們以Enron 數據集為例，閾值t=0.6，從5 萬條數據起，每次每組增加5 萬條，共6 組數據，分別運行4 種算法以觀察它們的運行時間與數據子集大小的關系.如圖6 所示，隨著數據子集大小的增加，TELP-SJ 的運行時間增長速度低于另外3 種算法，可擴展性最好.

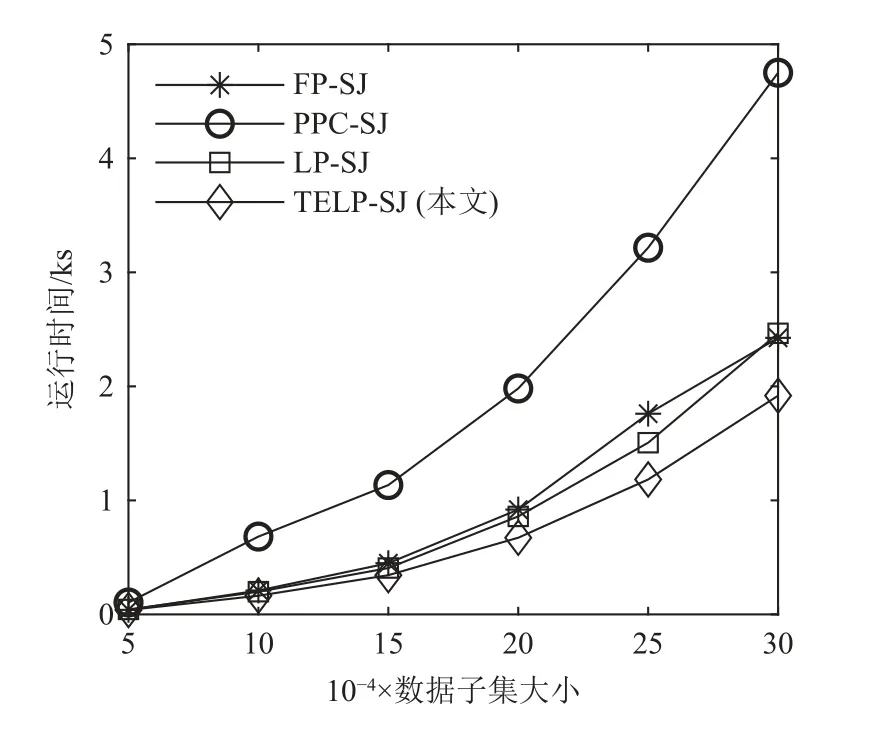
Fig.6 Relationship between FP-tree*-SJ’s running time and the size of Enron’s sub-datasets圖6 FP-tree*-SJ 的運行時間與Enron 數據子集大小的關系

2） 內存占用峰值

圖7 展示了闕值t= 0.6 時4 種算法運行期的內存占用率.由圖7（a）（b）可見，4 種FP-tree*-SJ 算法運行期在facebook30w 和kosarak30w 數據子集上的內存占用率峰值相近，圖7（c）（d）則顯示在Enron30w和acciden30w 數據集上，FP-SJ 的內存占用率峰值最高，PPC-SJ 相對較低和TELP-SJ 最低，這說明TELPSJ 使用數組存儲了更多的元素，具有較好的壓縮比，而PPC-tree 因為使用N-lists 進行計算，不需要建立相同元素結點間的索引鏈，減少了內存開銷.

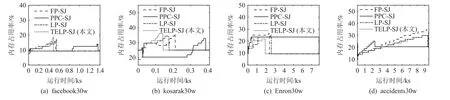
Fig.7 Memory usage of FP-tree*-SJ (t = 0.6)圖7 FP-tree*-SJ 的內存占用率（t = 0.6）

3.2 FastTELP-SJ 算法與TELP-SJ 算法的比較

本節我們以TELP-tree 為例，以FastTELP-SJ 相對TELP-SJ 的運行時間加速比及內存占用峰值評估MapReduce 對基于FP-tree*的集合相似度自連接算法的加速效果.

實驗將FastTELP-SJ 和TELP-SJ 分別運行在4 個數據集的子集上，圖8 描繪了2 種算法的相對加速比.其中數據子集大小始于5 萬條，每次每組增加5萬條，共6 組數據，閾值t分別設置為0.6 和0.9.由圖8 可見，當閾值t= 0.6 時，隨著數據子集大小的增加，相對加速比加大.FastTELP-SJ 相對于TELP-SJ 的相對加速比在accidents 數據子集上高達10，且在facebook 和Enron 數據子集上相對加速比的增長近似于線性.當閾值t= 0.9 時，當數據子集大小等于3 萬條時，相對加速比在Enron 和accidents 數據子集上分別約為2 和7，可見采用并行分布式計算框架MapReduce 可加速基于FP-tree*的集合相似度自連接計算.

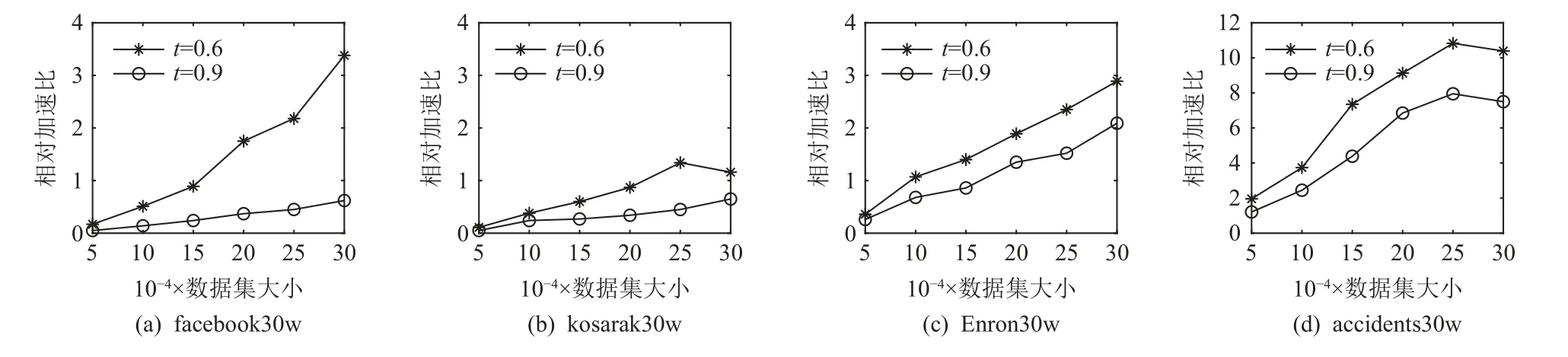
Fig.8 Relative speedup of FastTELP-SJ and TELP-SJ圖8 FastTELP-SJ 與TELP-SJ 的相對加速比

當數據子集比較小時，如圖8 中數據集大小小于15 萬條時，FastTELP-SJ 和TELP-SJ 算法的相對加速比在facebook, kosarak, Enron 等數據子集上都小于1.同時，在所有kosarak 數據子集上的相對加速比增長都緩慢，且小于1.5.這是因為該數據集的 |A(x′)|和(|X(a′i)|)偏低，如圖9 所示，轉置后數據子集的規模和維度都不大，相當于小數據集.同理，當閾值t=0.9 時，大部分數據在第1 階段過濾中被過濾掉，規模減小后的候選集變成了小數據集，因此，2 種算法的相對加速比在facebook 和kosarak 數據子集中都小于1.這是因為基于并行分布式計算框架MapReduce 的計算有額外的運行期開銷，包括數據劃分、合并、重新分配、排序等，當數據集比較小時，額外地運行其開銷抵消甚至超過降低切分數據并行計算帶來的提升.此時，TELP-SJ 比FastTELP-SJ 的運行效率高.

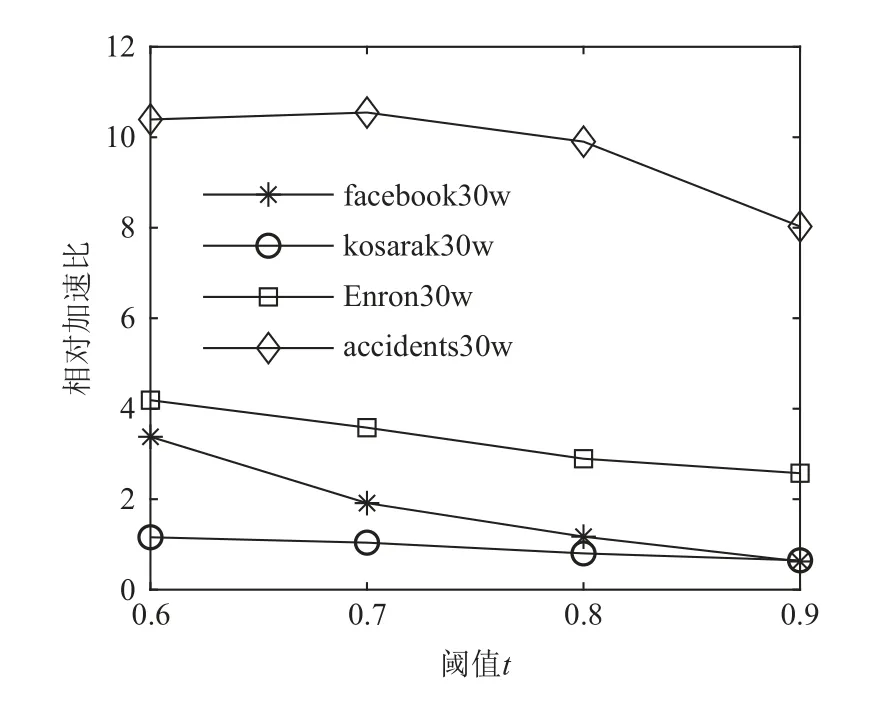
Fig.9 Relationship between relative speedups of FastTELP-SJ and TELP-SJ, and the threshold圖9 FastTELP-SJ 和TELP-SJ 的相對加速比與閾值的關系

另外，圖9 描繪了2 種算法的相對加速比與閾值t的關系.數據子集大小均為30 萬條，閾值t設置為 0.6 ～0.9.從圖9 可以看出FastTELP-SJ 和TELP-SJ的相對加速比在4 個數據集上都大于1，且隨著閾值的減小，相對加速比在不斷增大.這是因為在閾值減小時，第1 階段過濾后得到的候選集規模變大，需要進行兩兩交集大小計算的集合對個數增多，利用并行分布式計算框架MapReduce 的FastTELP-SJ 能使用更多計算資源完成計算，因而減小計算耗時.

圖10 描 繪 的 是 闕 值t=0.6時FastTELP-SJ 和TELP-SJ 在4 個數據子集上的運行期內存占用率，從圖10 可見，除了在enron30w 數據子集上兩者的內存占用率峰值基本相等外，在其他3 個子集上FastTELP-SJ的內存占用率峰值接近于TELP-SJ 的 1/2，即采用并行分布式計算框架MapReduce 可減少單個節點的內存負載.

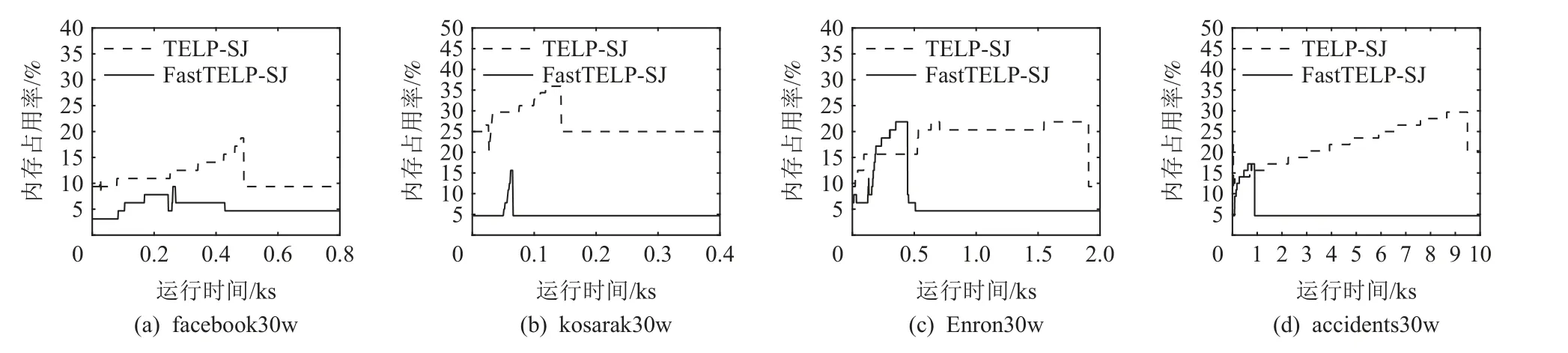
Fig.10 Memory usage of FastTELP-SJ and TELP-SJ (t = 0.6)圖10 FastTELP-SJ 與TELP-SJ 的內存占用率（t = 0.6）

3.3 FastTELP-SJ 與現有經典算法的比較

從3.1 節和3.2 節的實驗結果可見，FastTELP-SJ在處理大規模集合相似度自連接計算時相較于基于其他FP-tree*-SJ 算法運行效率最高.RP-PPJoin 和FSJoin 是基于MapReduce 的集合相似度自連接算法的代表.另外，最近提出的位圖過濾[12]在單機和GPU系統上運行均展現了它的有效性.在本節，為了更全面地評估FastTELP-SJ 的性能，本文同時設計并實現基于位圖過濾策略的RP-PPJoin，記為RP-PPJoin +Bitmap.我們將通過FastTELP-SJ 與RP-PPJoin, RPPPJoin + Bitmap, FS-Join 這4 種算法的比較實驗評估FastTELP-SJ 的性能.

1） 運行時間

首先將這4 種算法運行在facebookb30w, kosarak 30w, Enron30w, accidents30w 這4 組 數 據 集 上.閾 值t的取值范圍為 0.6 ～0.9.圖11 展示4 種算法隨著閾值t的提高運行時間的變化，可以看到通過使用位圖過濾，RP-PPJoin + Bitmap 在facebookb30w, kosarak30w,Enron30w 上的運行效率都得到提高.而FastTELP-SJ的運行時間在這3 個數據集上都優于其他3 種算法，尤其在閾值t＜0.7 時運行時間明顯降低很多.這主要是TELP-SJ 將數據壓縮在內存中進行計算，減少了I/O 次數，減小了候選集和降低了計算復雜度.而此時RP-PPJoin, RP-PPJoin + Bitmap, FS-join 算法產生較大候選集，其O(kn2)的高復雜度驗證計算延長了運行時間.尤其對accidents30w，當t≤0.85時，FS-Join 無法在當前計算環境中完成計算，當t＜0.7時，RP-PPJoin和RP-PPJoin+Bitmap 的運行時間大幅度升高，而FastTELP-SJ 的運行時間增長不多，運行效率最高.

Fig.11 Relationship between running time of FastTELP-SJ, RP-PPJoin, RP-PPJoin+Bitmap and FS-Join, and the threshold圖11 FastTELP-SJ 和RP-PPJoin, RP-PPJoin+Bitmap, FS-Join 的運行時間與閾值的關系

圖12 描繪了這4 種算法的運行時間與數據子集大小的關系，以accidents 數據集為例，閾值t分別設置為0.6 和0.9.其中，0.6 代表了低閾值情況，而0.9代表了較高閾值的情況.數據子集大小始于5 萬條、每次每組增加5 萬條，取6 組數據，分別運行這4 種算法并觀察它們的運行時間與數據子集大小的關系.如圖12（a）所示，當t=0.6時，FastTELP- SJ 的運行時間低于另外3 種算法，且其運行時間隨數據增長呈線性增長，可擴展性優于另外3 種算法.當t=0.9時，高閾值下各算法應用過濾策略過濾了大量相似度低于閾值的候選集合對.此時，FastTELP-SJ 的運行期開銷如建樹時間等導致它的總運行時間高于RPPPJoin 和RP-PPJoin + Bitmap，但仍然低于FS-Join，如圖12（b）所示，這個結果也與圖10 中t值較大時的結果一致.

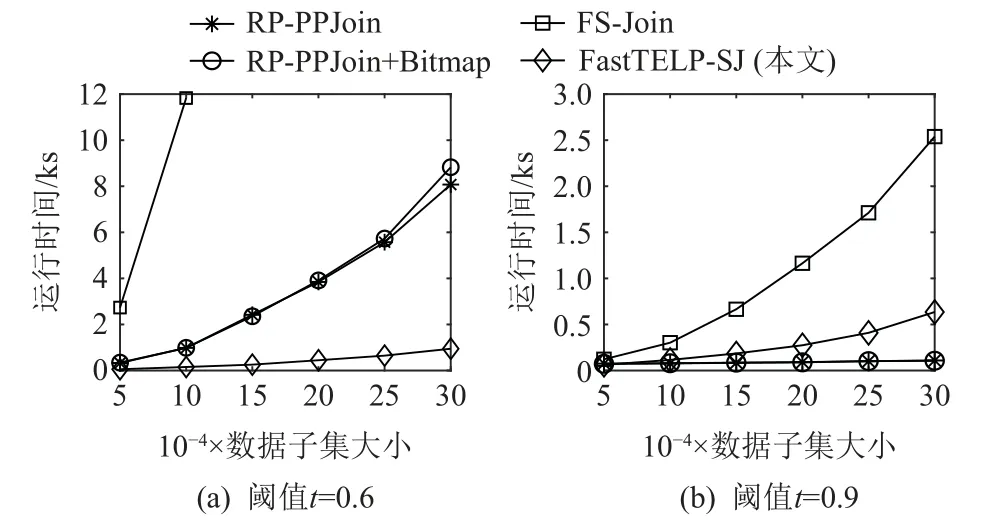
Fig.12 Relationship between running time of FastTELP-SJ,RP-PPJoin, RP-PPJoin+Bitmap and FS-Join, and the size of accidents’ sub-datasets圖12 FastTELP-SJ, RP-PPJoin, RP-PPJoin + Bitmap,FS-Join 的運行時間與accidents 數據子集大小的關系

最后，我們評估這4 種算法的運行時間與集群規模的關系，其中，集群規模為集群節點個數.實驗以facebook30w 數據集為例，閾值t設置為0.6，集群規模起始計算節點為2，依次增加2 個直至16 個，分別運行4 種算法并觀察它們的運行時間與集群規模的關系.圖13 描繪了實驗結果，隨著集群節點個數的增加，相比于RP-PPJoin, RP-PPJoin+Bitmap, FSJoin 和FastTELPSJ 運行時間的變化速率下降得更慢.這說明相較于其他3 種算法，FastTELP-SJ 的擴展性最好.

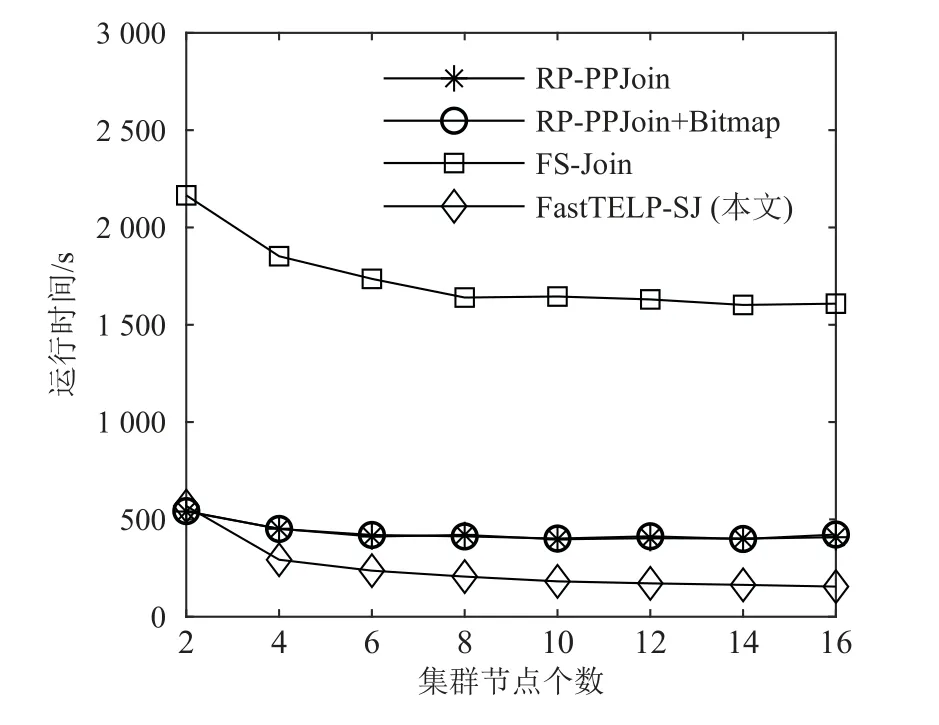
Fig.13 Relationship between running time of FastTELP-SJ,RP-PPJoin, RP-PPJoin+Bitmap and FS-Join, and the cluster’s size圖13 FastTELP-SJ, RP-PPJoin, RP-PPJoin + Bitmap, FSJoin 的運行時間與集群規模的關系

2） 內存占用率

圖14 描繪了4 種算法在facebookb30w, kosarak 30w, Enron30w, accidents30w 這4 組數據子集進行集合相似度自連接計算過程中的內存占用率，其中，FastTELP-SJ 在 處 理kosarak30w 和Enron30w 時 內 存占用率峰值分別是其他3 種算法的2～3 倍，因為TELP-tree 在其任務2 的函數reduce運行過程中常駐內存，這跟第1, 2 節的分析一致.但RP-PPJoin 和FSJoin 的候選集大，也有可能出現內存占用率高的情況，如圖14（a）（d）.同時RP-PPJoin+Bitmap 的內存占用率峰值始終最大，這是因為該算法需要為每個集合構造相應的位圖并保存在內存中進行計算.

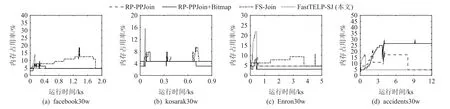
Fig.14 Memory usage of four algorithms （t = 0.6）圖14 4 種算法的內存占用率（t = 0.6）

3） 磁盤使用量

圖15 描繪了4 種算法在facebookb30w，kosarak 30w，Enron30w，accidents30w 這4 組數據子集上進行集合相似度自連接計算過程中的磁盤使用量.當閾值t= 0.6 時，FastTELP-SJ 在處理facebook30w，kosarak-30w，accidents30w 這3 個數據子集時的磁盤讀寫量最低，因為它的驗證計算都在內存中完成，減少了I/O，此結論與第1, 2 節的分析和3.3.1 節運行時間相關的實驗結果分析相一致.尤其是RP-PPJoin 和RP-PPJoin+Bitmap，因它們可能產生重復驗證的冗余候選集，磁盤使用量最大，見圖15（c）（d）.而當闕值t增大時，如t=0.9時，由于過濾策略的應用，大量數據被過濾，各個算法的磁盤使用量都降低，差別也減少.

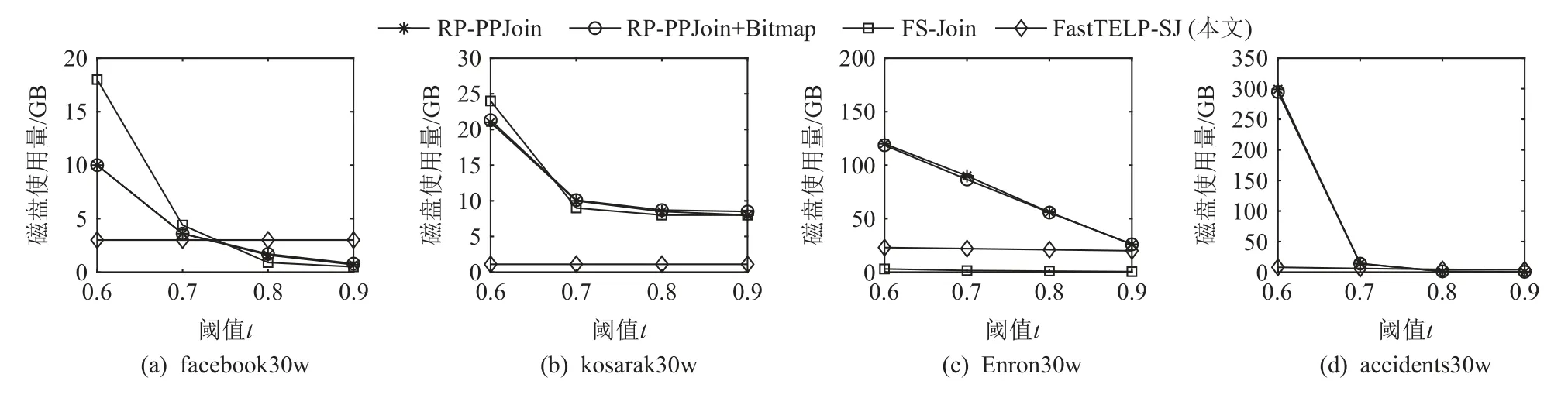
Fig.15 Disk usage amount of four algorithms圖15 4 種算法的磁盤使用量

3.4 小 結

基于3.1～3.3 節的實驗結果比較，當閾值t比較高時，如在我們的實驗環境和數據下，t＞0.8時， 4 種算法的執行性能差別不大.當閾值t比較低時，我們有4 點實驗結論：

1） 高維大規模集合相似度自連接計算中TELPSJ 的運行效率最好且具有較好的可擴展性.

2） 低維大規模集合相似度自連接計算中PPCSJ 的運行效率最好.

3） 高維大規模集合相似度自連接計算中基于并行分布式計算模型MapReduce 和TELP-tree 設計的算法FastTELP-SJ 相對于TELP-SJ 有較好的加速比.

4） 大規模集合相似度自連接計算中FastTELPSJ 的運行效率優于現有基于MapReduce 的3 類算法RP-PPJoin, RP-PPJoin + Bitmap, FS-Join.

4 結束語

數據的增長、集合規模的加大給現有集合相似度自連接算法帶來挑戰.基于MapReduce 的并行分布式集合相似度自連接加速了計算，但當閾值較低時現有算法生成了較大規模的候選集，執行效率依然不理想.

為此，本文提出并設計采用頻繁模式樹及其派生結構FP-tree*加速集合相似度自連接算法：1）設計面向基于FP-tree*的集合相似度自連接算法及加速其計算的2 階段過濾規則，減小FP-tree*的規模并提高樹遍歷效率；2）提出并構建面向集合相似度自連接的遍歷效率更高的FP-tree 派生結構-線性頻繁模式樹結構TELP-tree 及基于其的算法TELP-SJ；3）設計基于MapReduce 和TELP-tree 的集合相似度自連接算法FastTELP-SJ.基于4 組真實應用數據集，通過3組比較實驗從運行時間、內存占用率、磁盤使用量等方面進行對比實驗來評估FastTELP-SJ 的性能，實驗結果展現了FastTELP-SJ 較好運行性能和可擴展性.

FastTELP-SJ 算法將數據壓縮在內存中進行計算，帶來構建樹和銷毀樹等運行期內存管理開銷，同時，FastTELP-SJ 算法包含2 次MapReduce 任務，帶來運行期流程管理開銷.經調研，文獻[39-40]設計了一種基于生命周期的內存管理框架Deca，通過自動分析用戶定義的函數和數據結構，預測其生命周期.基于該預測分配和釋放空間可提高系統垃圾回收效率，進而提高內存使用率.另外，文獻[41-42]提出了一種面向流數據和迭代任務流程管理降低能耗的資源共享框架F3C.我們將進一步研究如何結合有效的內存管理、流程管理框架構建綠色高效的集合相似度連接計算.

作者貢獻聲明：馮禹洪發現問題、定義問題、提出算法思路和實驗方案；吳坤漢、黃志鴻、馮洋洲負責完成算法設計、實現、性能評估；陳歡歡、白鑒聰、明仲優化算法和實驗方案.所有作者共同完善國內外研究現狀調研、完成論文的撰寫和修改.