“雙碳”目標下綠色金融助力經濟低碳轉型的機制研究
——基于綠色索羅模型

孟 禹 郭 凱，2 張瑩瑩

（1.東北財經大學，大連 116025；2.遼寧（大連）自貿區研究院，遼寧 116025）

內容提要：本文基于2006 年-2020 年30 個省份面板數據，采用系統GMM 模型實證分析和驗證了綠色金融助力經濟低碳轉型的作用機制，進一步探究了不同碳排放水平下，綠色金融助力經濟低碳轉型的作用機制是否存在異質性。研究發現，綠色金融可以助力經濟低碳轉型；在當前的能源結構和綠色全要素生產率水平下，綠色金融可以同時通過能源結構和綠色全要素生產率的調節機制助力經濟低碳轉型。但能源結構和綠色全要素生產率的調節機制存在區域異質性，在高碳排放地區能源結構的調節機制沒有發揮出來，綠色全要素生產率的調節機制為負向，在低碳排放地區能源結構和綠色全要素生產率均發揮了正向的調節機制。

一、引言

2020 年，我國提出“雙碳”目標，表明了大力推動綠色低碳發展的決心。綠色金融依據國家環保政策可以為清潔能源、綠色環保等改善環境、應對氣候變化的項目在投融資、運行、風險管理方面提供有針對性的金融服務，可以引導經濟向低碳發展方向轉型和升級，是實現經濟低碳轉型不可或缺的重要力量。國內外學者研究均證實了綠色金融是實現經濟可持續發展、協調人與自然的重要保障（王瑤和曹暢，2015；Soundarrajan 和Vivek，2016；朱四榮，2019）。綠色金融具有節能減排效應，但綠色金融是否助力了經濟低碳轉型？綠色金融發揮經濟低碳轉型作用的具體機制是什么？都是急需探究的重要議題。為此，本文從理論和實證兩個方面系統剖析了綠色金融助力經濟低碳轉型的作用機制。本文的創新之處：（1）研究視角的創新。為實現“雙碳”目標需要推動經濟低碳轉型，本文以現實問題為導向，將研究視角放在綠色金融助力經濟低碳轉型上，在豐富相關文獻的基礎上，可以為實現2030 年“碳達峰”，2060 年“碳中和”提供研究啟示。（2）研究方法的創新。本文在Brock 和Taylor（2010）構建的綠色索羅模型基礎上，創新性地引入綠色金融因素進行模型拓展，為分析綠色金融助力經濟低碳轉型提供一個改進的理論分析框架。

二、理論分析與研究假設

本文在Brock 和Taylor（2010）構建的綠色索羅模型的基礎上，引入綠色金融變量進行理論拓展。模型的主要假設：污染排放是生產過程中的副產品（亦即將污染作為一種非期望產出），模型的主要設定如下：

式中，Y 為總產出水平；K、B 和L 分別為考慮了環境治理的“綠色”資本存量、勞動的有效性和勞動力數量；G 為綠色金融治理環境污染的投入量，vG為綠色金融治理環境污染的投入量在總資本中的占比；R 為不可再生能源，vR為不可再生能源的消耗量在總資本中的占比；I 為總投資；s 和δ 分別為儲蓄率和折舊率；、和分別為“綠色”資本存量、勞動有效性和勞動力數量隨時間的變化率；gB為勞動有效性（亦即用于生產的技術水平）的增長率；n 為外生的人口增長率；E 為污染排放總量；Ω 表示環保技術水平（綠色全要素生產率），大小為gA；a 為一個強度減排函數，a'＜0 而a''＞0。

假設生產函數是柯布-道格拉斯且規模報酬不變。將模型的主要變量（Y、K、E）進一步整理為單位有效勞動的形式（用小寫字母表示）：

將主要變量轉換為單位有效勞動的水平，進一步計算其增長率：

e 與碳排放總量E 之間的關系如下：

根據公式（2）-（16）得到碳排放總量的增長率：

當最終經濟達到穩態時，單位有效勞動資本存量k 的增速將為0，污染排放總量以恒定速度gE=n+gB+gR-(gA+gG)下降，在T 時點達到峰值后再逐漸下降的過程，如圖1 所展示。從圖1 可以看出，當不考慮綠色金融時，單位有效勞動資本存量的增長率gk=ska-1-(n+δ+vR+gB)對應于圖1 中的曲線Ⅰ，如果碳排放總量的增長率等于零時對應的gk可以表示為：對應于圖1 中的直線Ⅲ，與曲線Ⅰ相交于點A；當考慮綠色金融因時，單位有效勞動“綠色”資本存量的增長率gk=ska-1-(n+δ+vG+vR+gB)對應于圖1 中的曲線Ⅱ，如果碳排放總量的增長率等于零（g'EE=0） 時對應的 gk可以表示為：對應于圖1 中的直線Ⅳ，與曲線Ⅱ相交于點B。因此，綠色金融使曲線由Ⅰ移動到曲線Ⅱ，曲線由Ⅲ移動到曲線Ⅳ，對應的碳排放強度曲線由Ⅴ移動到Ⅵ。基于上述分析，本文提出以下假設：

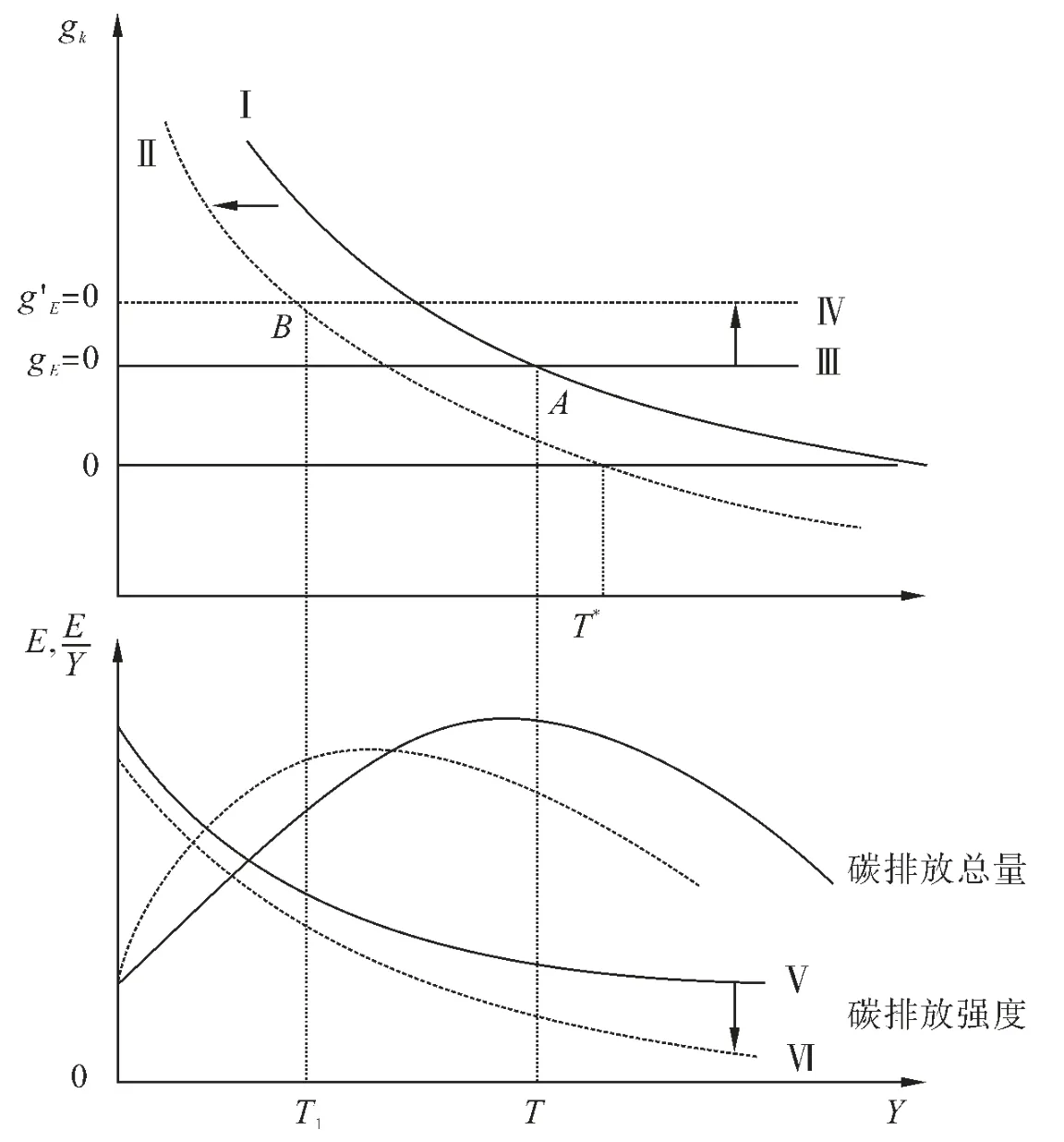
圖1 基于綠色索羅模型的環境庫茲涅茲曲線

H1：“雙碳”目標下，綠色金融可以助力經濟低碳轉型。

（一）基于能源結構的調節機制

綠色金融對碳排放強度的影響如圖2 所示。從圖2 可以看出，在包含綠色金融與碳排放強度的綠色索羅模型中，當不減少不可再生能源的消費（gR）時，單位有效勞動“綠色”資本存量的增長率gk=ska-1-(n+δ+vG+vR+gB)對應于圖2 中的曲線Ⅰ，如果碳排放總量的增長率等于零時對應的gk可以表示為：對應于圖2 中的直線Ⅲ，與曲線Ⅰ相交于點A；當減少不可再生能源的消費（gR）時，單位有效勞動“綠色”資本存量的增長率g'k=ska-1-(n+δ+vG+vR′+gB)對應于圖2 中的曲線Ⅱ，如果碳排放總量的增長率等于零時對應的gk可以表示為：，對應于圖2 中的直線Ⅳ，與曲線Ⅱ相交于點B。又因為根據公式（17）碳排放總量的增長率gE=agk+n+gB+gR-(gA+gG)，那么減少不可再生能源的消費（gR）意味著相同的經濟產出伴隨著更少的碳排放。因此，在能源結構的調節下，綠色金融通過調整使曲線由Ⅰ移動到曲線Ⅱ，曲線由Ⅲ移動到曲線Ⅳ，對應的碳排放強度曲線由Ⅴ移動到Ⅵ。基于上述分析，本文提出以下假設：

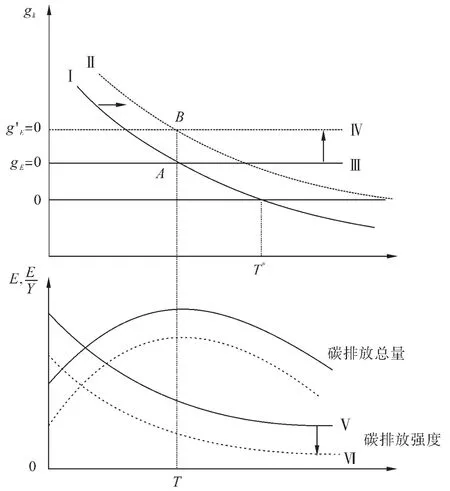
圖2 能源結構調節下的環境庫茲涅茲曲線

H2：“雙碳”目標下，綠色金融通過能源結構（降低不可再生能源的消費）的調節機制可以助力經濟低碳轉型。

（二）基于綠色全要素生產率的調節機制

綠色金融對碳排放強度的影響如圖3 所示。從圖3 可以看出，在包含綠色金融與碳排放強度的綠色索羅模型中，當還未提高綠色全要生產率（gA）時，碳排放總量的增長率等于零時對應的gk可以表示為：對應于圖3 中的直線Ⅰ，與gk曲線相交于點A；當提高了綠色全要生產率（gA）時，碳排放總量的增長率等于零（g'E=0）時對應的gk可以表示為：對應于圖3 中的直線Ⅱ，與gk曲線相交于點B。又因為無論是否提高綠色全要生產率（gA），對單位有效勞動“綠色”資本存量的增長率gk=ska-1-(n+δ+vG+vR+gB)沒有影響。因此，在綠色全要素生產率的調節下，綠色金融通過調整使曲線由Ⅰ移動到曲線Ⅱ，對應的碳排放強度曲線由Ⅴ移動到Ⅵ。基于上述分析，本文提出以下假設：

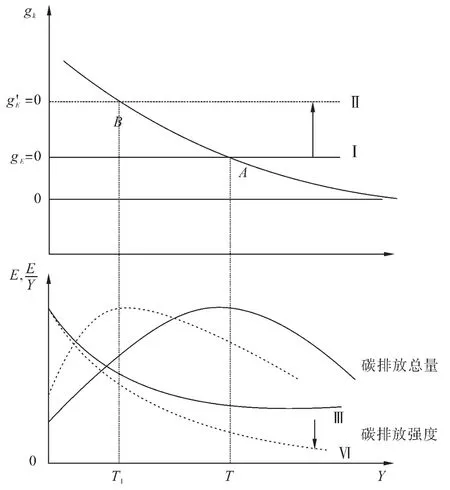
圖3 綠色全要素生產率調節下的環境庫茲涅茲曲線

H3：“雙碳”目標下，綠色金融通過綠色全要素生產率的調節機制可以助力經濟低碳轉型。

三、研究設計

（一）實證模型

本文研究綠色金融助力經濟低碳轉型的作用機制，由于經濟增長存在慣性，上期經濟增長會對當期的經濟增長產生影響，同理上期的碳排放會對當期的碳排放產生影響，顯然會存在滯后的被解釋變量與誤差項相關，直接進行OLS 估計是有偏且不一致的。廣義矩估計（GMM）可以允許誤差項存在異方差和序列相關，能通過將變量的滯后項作為工具變量解決模型中的內生性問題，顯然GMM 模型更適用于本文的研究。因此，本文采用GMM 模型，模型構建如下：

其中，下標i 為省份標識，t 為年份標識，i=1，2，…30；t=1，2…；α1…α5為常數項，β11…β55均為待估系數；CGit表示GDP 碳排放強度，GFit表示綠色金融，ESit表示能源結構；GTFPit表示綠色全要素生產率；Zit表示控制變量的集合；ηi代表個體效應，μt代表時間效應，εit為殘差項。

（二）變量選擇與數據來源

1.被解釋變量

GDP 碳排放強度。本文選擇GDP 碳排放強度（CG=CO2/GDP）來衡量經濟低碳轉型。

2.解釋變量

（1）綠色金融。本文借鑒高錦杰（2021）的做法，選取了綠色信貸、綠色投資、綠色保險、政府支持四個維度，如表1 所示。數據來源于各省份《統計年鑒》以及《中國保險年鑒》。

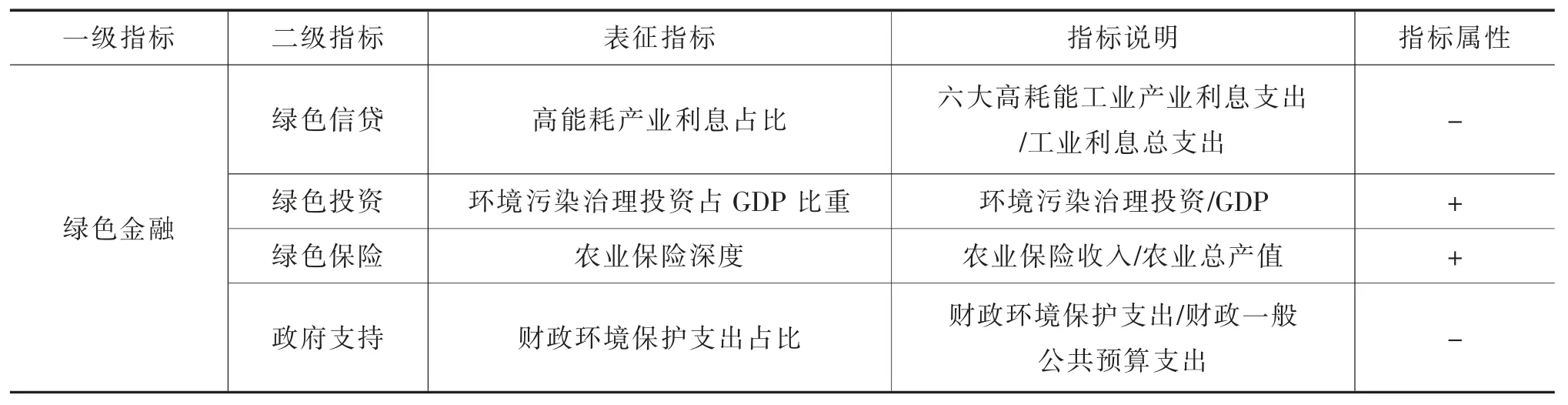
表1 綠色金融指標構建

（2）能源結構。本文采用清潔能源與高耗能能源消費量的比值來衡量能源結構，記為ES。數據來源于《中國能源統計年鑒》。

（3）綠色全要素生產率。本文借鑒Tone（2001）和Oh（2010）采用SBM-GML 方法測算我國30 個省（市）的綠色全要素生產率，記為GTFP。本文選取的投入指標如表2 所示，樣本數據均來源于《中經網統計數據庫》。

表2 采用SBM-GML 方法測算各省GTFP 的投入與產出指標

3.控制變量。借鑒現有文獻，本文控制變量的選擇如表3 所示。樣本數據均來源于《中經網統計數據庫》。

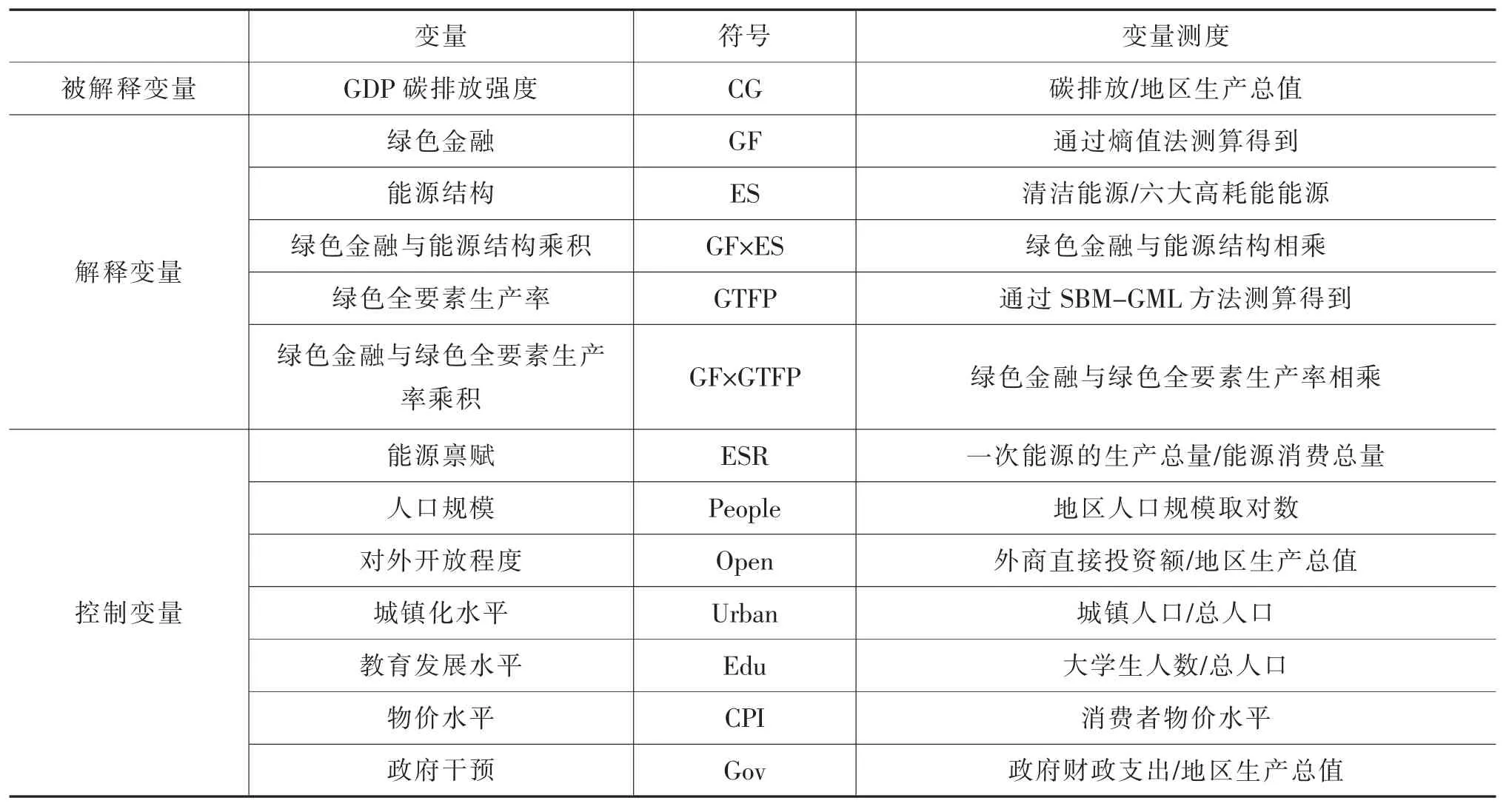
表3 變量定義及測度

（三）變量的描述性統計

本文的數據結構為2006 年-2020 年的省域數據，表4 是本文樣本數據的描述性統計。從表中可以看出GDP 碳排放強度（CG）、能源稟賦（ESR）、對外開放程度（Open）和物價水平（CPI）的最小值與最大值差異較大。

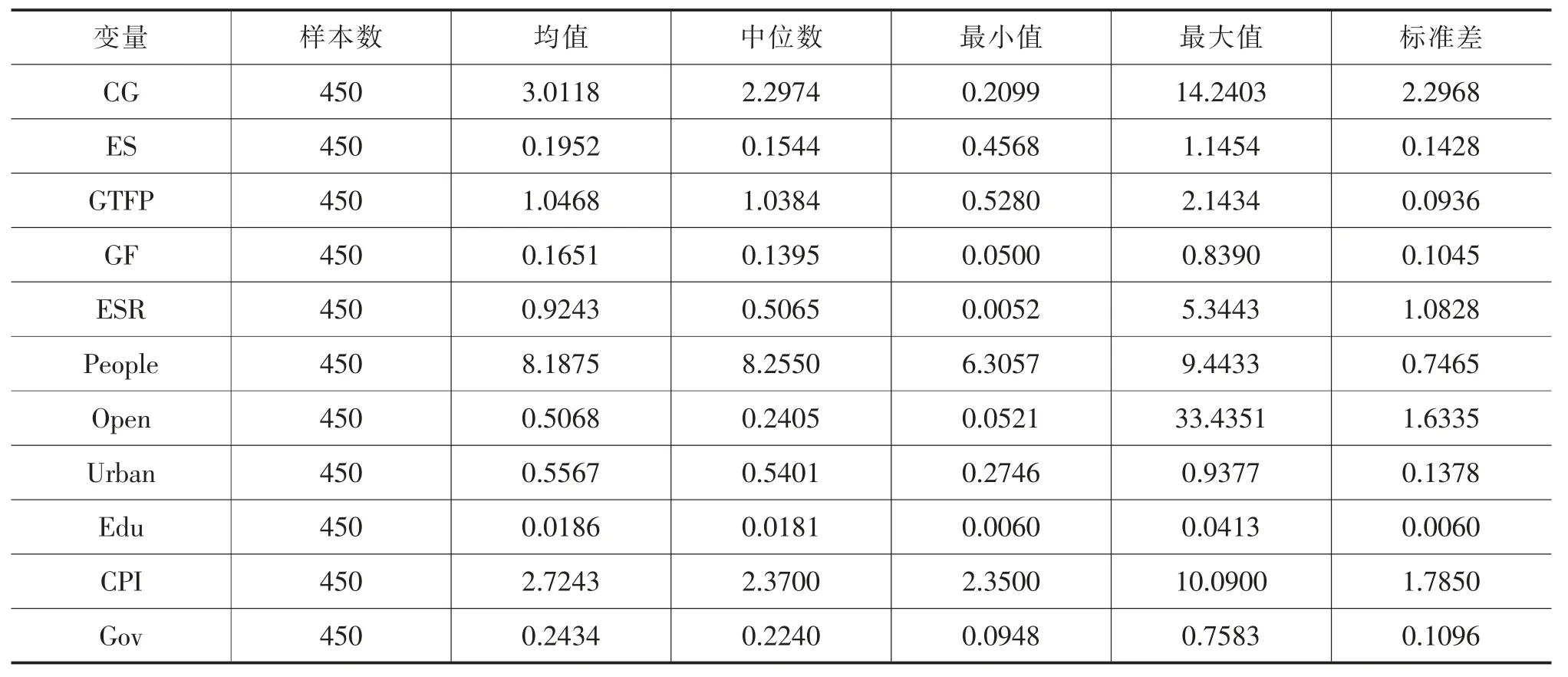
表4 樣本數據的描述性統計

四、實證結果分析

（一）面板單位根檢驗

表5 是各變量的單位根檢驗結果。從表中看出，各變量均在1%的統計水平上顯著，因此，本文的樣本數據均滿足平穩性條件。

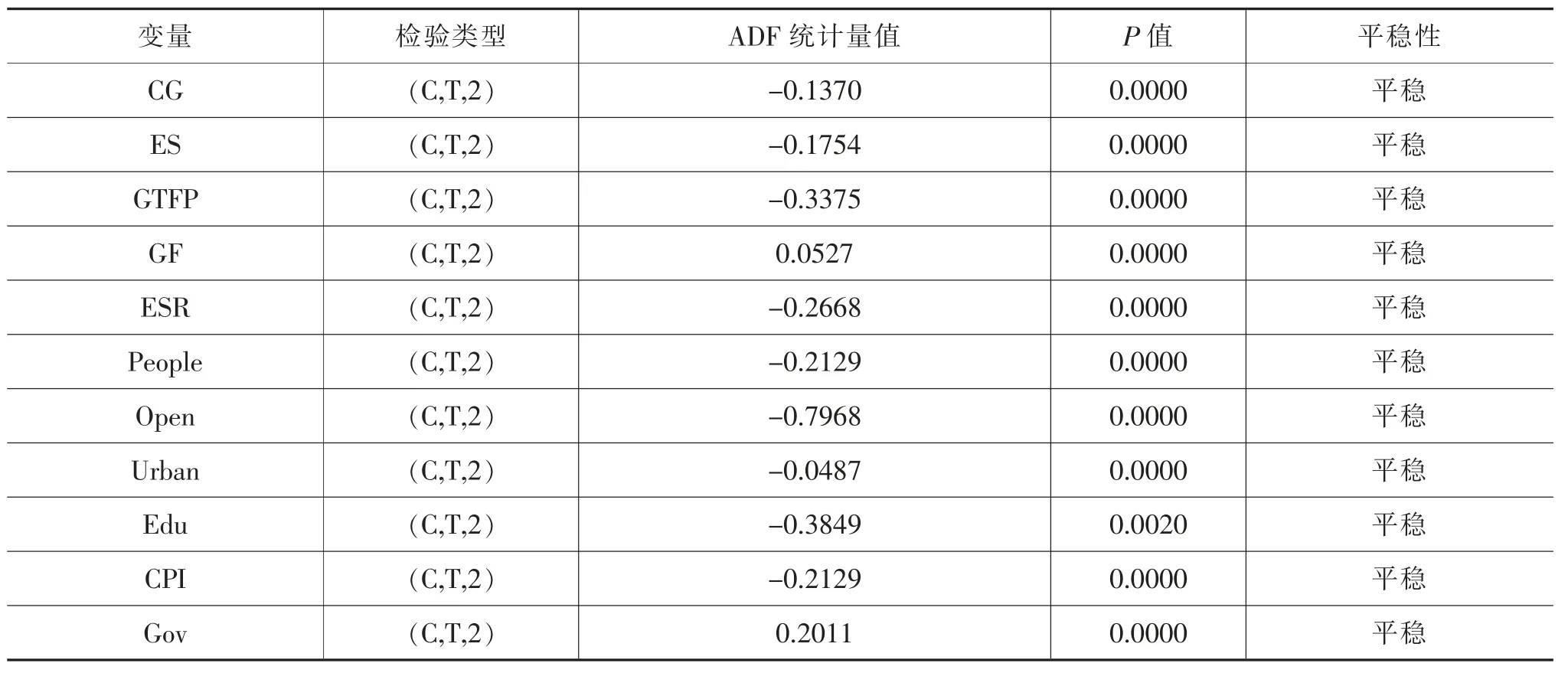
表5 ADF 單位根檢驗結果

（二）實證結果分析

表6 中的第（1）列是綠色金融對GDP 碳排放強度的估計結果。從表中可以看出，綠色金融對GDP碳排放強度的回歸系數為-3.0351，在1%的統計水平上顯著，說明綠色金融可以顯著降低GDP 碳排放強度。由此，假說H1 得到驗證。

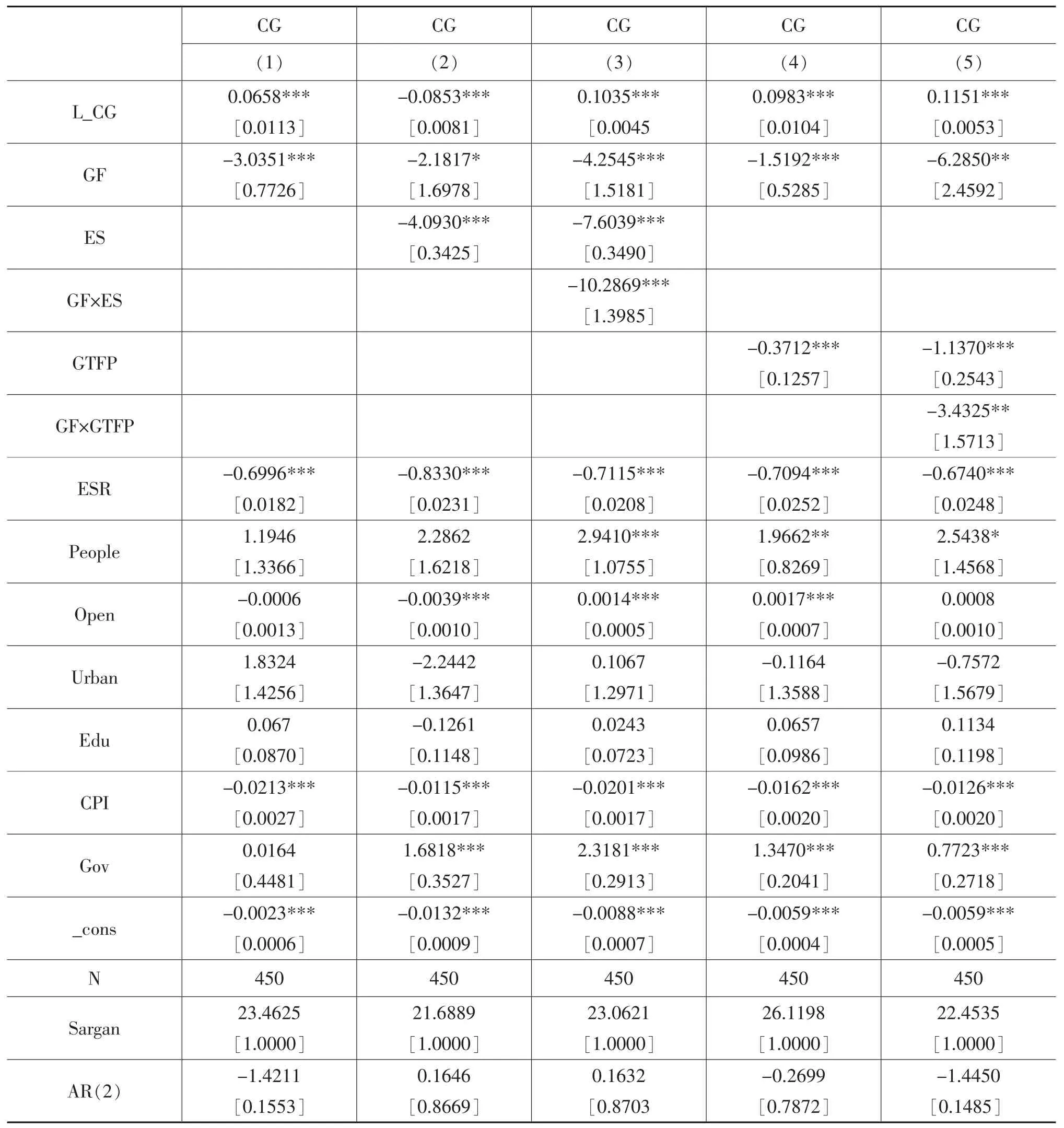
表6 全樣本系統GMM 的實證估計結果

從表6 中第（2）列可以看出，綠色金融對GDP碳排放強度的回歸系數為-2.1817，在10%的統計水平上顯著；能源結構對GDP 碳排放強度的回歸系數為-4.0903，在1%的統計水平上顯著。從表6 中第（3）列可以看出，綠色金融與能源結構的乘積項對GDP 碳排放強度的回歸系數為-10.2869，在1%的統計水平上顯著，說明能源結構的調節效應存在。同時，綠色金融對GDP 碳排放強度的回歸系數為-4.2525，在1%的統計水平上顯著；能源結構對GDP 碳排放強度的回歸系數為-7.6039，在1%的統計水平上顯著。說明通過能源結構的調節效應增強了綠色金融對GDP 碳排放強度的抑制作用。由此，假說H2 得到驗證。

從表6 中第（4）列可以看出，綠色金融對GDP碳排放強度的回歸系數為-1.5192，在1%的統計水平上顯著；綠色全要素生產率對GDP 碳排放強度的回歸系數為-1.1370，在1%的統計水平上顯著。從表中第（5）列可以看出，綠色金融與綠色全要素生產率的乘積項對GDP 碳排放強度的回歸系數為-3.4325，在5%的統計水平上顯著，說明綠色全要素生產率的調節效應存在。同時，綠色金融對GDP碳排放強度的回歸系數為-6.2850，在5%的統計水平上顯著；綠色全要素生產率對GDP 碳排放強度的回歸系數為-1.1370，在1%的統計水平上顯著。說明通過綠色全要素生產率的調節效應增強了綠色金融對GDP 碳排放強度的抑制作用。由此，假說H3得到驗證。

五、進一步分析

本文按照碳排放量的差別劃分出高碳排放地區和低碳排放地區①按照碳排放水平的不同進行劃分，碳排放前15 個省份為高碳排放地區，包括山東、河北、山西、江蘇、內蒙古、遼寧、河南、廣東、浙江、陜西、新疆、安徽、湖北、黑龍江、湖南；碳排放后15 個省份為高碳排放地區，包括四川、貴州、上海、吉林、福建、云南、廣西、江西、甘肅、寧夏、天津、重慶、北京、海南、青海。進行異質性分析。

（一）高碳排放地區

表7 中的第（1）列是高碳排放地區綠色金融對GDP 碳排放強度的估計結果，從表中可以看出，綠色金融對GDP 碳排放強度的回歸系數為-9.3141，在10%的統計水平上顯著，說明在高碳排放地區綠色金融可以顯著的降低GDP 碳排放強度。由此，假說H1 在高碳排放地區得到驗證。

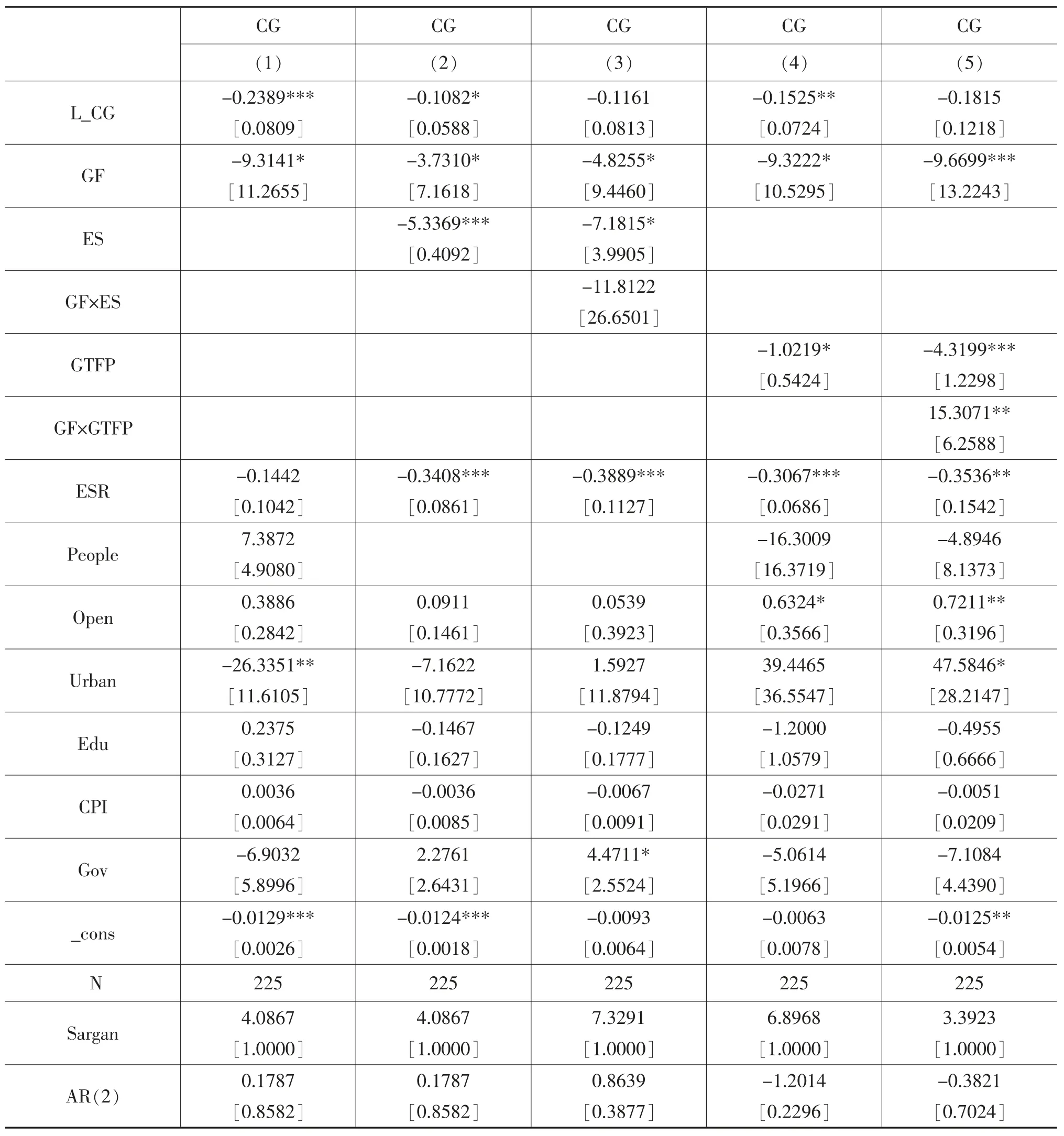
表7 高碳排放地區系統GMM 的實證估計結果

從表7 中第（2）列可以看出，高碳排放地區綠色金融對GDP 碳排放強度的回歸系數為-3.7310，在10%的統計水平上顯著；能源結構對GDP 碳排放強度的回歸系數為-5.3369，在1%的統計水平上顯著。從表7 中第（3）列可以看出，在高碳排放地區綠色金融與能源結構的乘積項對GDP 碳排放強度的回歸系數為-11.8122，但在統計水平上不顯著，說明在高碳排放地區能源結構的調節效應不存在。由此，假說H2 在高碳排放地區未得到驗證。

從表7 中第（4）列可以看出，高碳排放地區綠色金融對GDP 碳排放強度的回歸系數為-9.3222，在10%的統計水平上顯著；綠色全要素生產率對GDP碳排放強度的回歸系數為-1.0219，在10%的統計水平上顯著。從表中第（5）列可以看出，綠色金融與綠色全要素生產率的乘積項對GDP 碳排放強度的回歸系數為15.3071，在5%的統計水平上顯著，說明綠色全要素生產率的調節效應存在。同時，綠色金融對GDP 碳排放強度的回歸系數為-9.6699，在1%的統計水平上顯著；綠色全要素生產率對GDP 碳排放強度的回歸系數為-4.3199，在1%的統計水平上顯著。說明在高碳排放地區綠色全要素生產率的調節效應雖然存在，但綠色全要素生產率的正向調節機制沒有發揮出來。由此，假說H3 在高碳排放地區未得到驗證。

（二）低碳排放地區

表8 中的第（1）列是低碳排放地區綠色金融對GDP 碳排放強度的估計結果，從表中可以看出，低碳排放地區綠色金融對GDP 碳排放強度的回歸系數為-11.4110，在5%的統計水平上顯著，說明在低碳排放地區綠色金融可以十分顯著的降低GDP 碳排放強度。由此，假說H1 在低碳排放地區得到驗證。

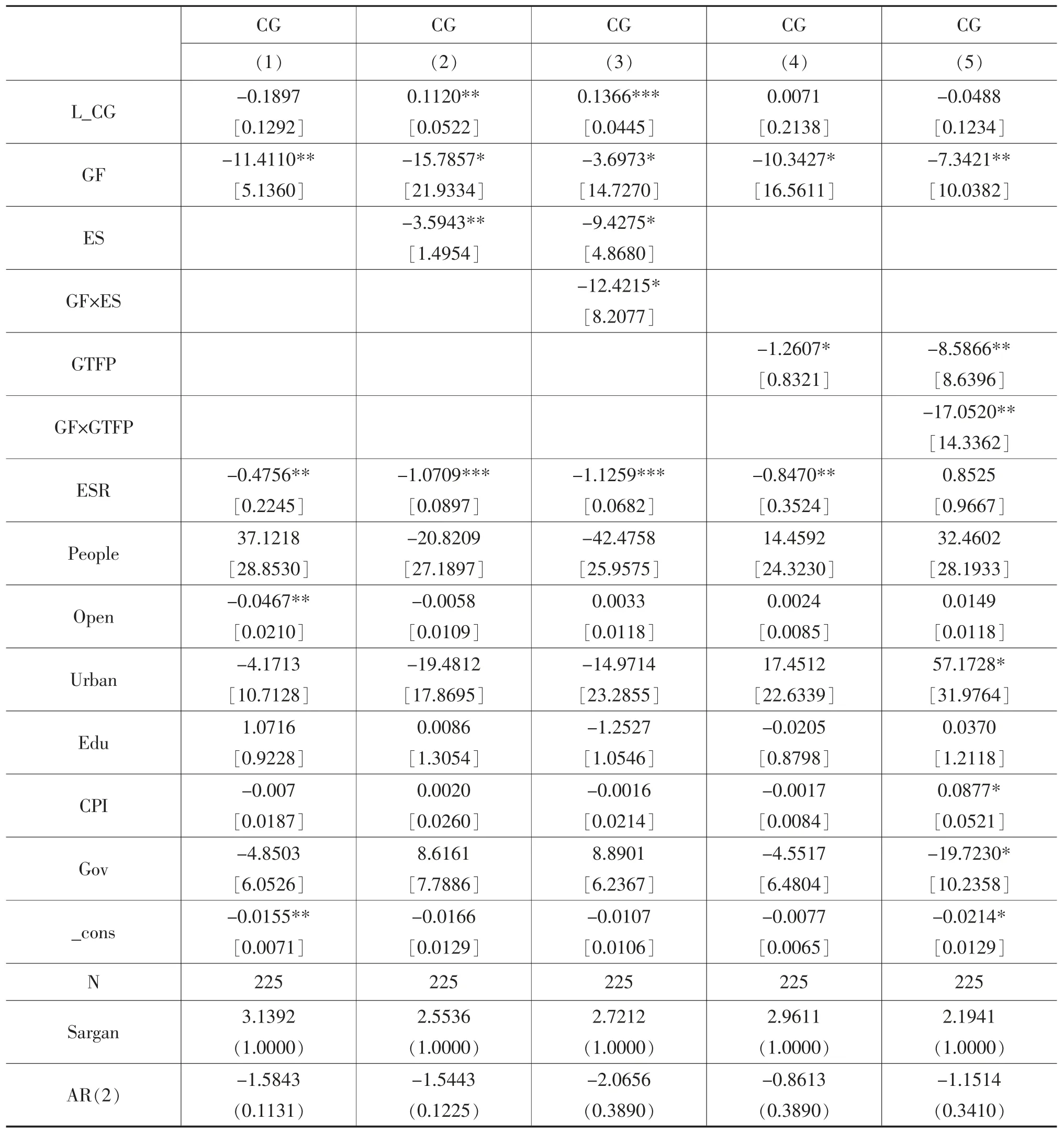
表8 低碳排放地區系統GMM 的實證估計結果

從表8 中第（2）列可以看出，低碳排放地區綠色金融對GDP 碳排放強度的回歸系數為-15.7857，在10%的統計水平上顯著；能源結構對GDP 碳排放強度的回歸系數為-3.5943，在5%的統計水平上顯著。從表中第（3）列可以看出，綠色金融與能源結構的乘積項對GDP 碳排放強度的回歸系數為-12.4215，在5%的統計水平上顯著，說明能源結構的調節效應存在。同時，綠色金融對GDP 碳排放強度的回歸系數為-3.6973，在10%的統計水平上顯著；能源結構對GDP 碳排放強度的回歸系數為-9.4275，在10%的統計水平上顯著。說明在低碳排放地區通過能源結構的調節效應增強了綠色金融對GDP 碳排放強度的抑制作用。由此，假說H2 在低碳排放地區得到驗證。

從表8 中第（4）列可以看出，低碳排放地區綠色金融對GDP 碳排放強度的回歸系數為-10.3427，在10%的統計水平上顯著；綠色全要素生產率對GDP碳排放強度的回歸系數為-1.2607，在10%的統計水平上顯著。從表中第（5）列可以看出，綠色金融與綠色全要素生產率的乘積項對GDP 碳排放強度的回歸系數為-17.0520，在5%的統計水平上顯著，說明綠色全要素生產率的調節效應存在。同時，綠色金融對GDP 碳排放強度的回歸系數為-7.3421，在5%的統計水平上顯著；綠色全要素生產率對GDP碳排放強度的回歸系數為-8.5866，在5%的統計水平上顯著。說明在低碳排放地區通過綠色全要素生產率的調節效應增強了綠色金融對GDP 碳排放強度的抑制作用。由此，假說H3 在低碳排放地區得到驗證。

（三）穩健性檢驗

本文采用更換估計方法和改變樣本容量的方法進行穩健性檢驗，得出的穩健性檢驗回歸結果與前文結論基本一致，說明本文的結論是較為可信的。由于篇幅限制，表未列出。

六、研究結論與政策建議

（一）研究結論

通過本文的研究得出以下結論：

一是綠色金融可以顯著的降低GDP 碳排放系數，即綠色金融可以助力經濟低碳轉型。在當前的能源結構和綠色全要素生產率水平下，綠色金融可以同時通過能源結構和綠色全要素生產率的調節作用助力經濟低碳轉型。

二是能源結構和綠色全要素生產率對綠色金融助力經濟低碳轉型的調節機制存在區域異質性。在高碳排放地區能源結構和綠色全要素生產率的調節機制沒有發揮出來；在低碳排放地區能源結構和綠色全要素生產率在綠色金融助力經濟低碳轉型中的正向調節機制都得到了發揮。

（二）政策建議

首先，強化綠色發展理念，積極完善綠色金融體系。綠色金融是實現經濟低碳轉型不可或缺的重要力量，應積極推進綠色金融的發展，一方面，要強化綠色發展理念，創新綠色金融產品，將金融產品設計逐漸向清潔能源拓展。另一方面，還應盡快完善綠色金融體系的建立，積極引導不同類型的金融機構滲透到綠色金融的發展當中，鼓勵并引導證券、基金、信托等其他金融機構在綠色金融發展中發揮積極作用。

其次，加快清潔能源開發，促進能源消費結構低碳化。能源結構在綠色金融助力經濟低碳轉型過程中發揮著重要的調節作用，雖然我國已經開始關注對能源結構的調整，但由于能源稟賦的差異，不同省份的調整效果還存在不小差異。我國應充分利用兩個市場、兩種資源，鼓勵各行各業使用天然氣等清潔能源，降低對化石能源的依賴，優化一次能源消費結構，支持新能源產業的發展，積極推進能源結構調整，進一步實現能源利用的高效化、清潔化。

最后，提高技術創新水平，促進經濟增長方式向集約型轉變。綠色全要素生產率同樣在綠色金融助力經濟低碳轉型過程中發揮著重要的調節作用，綠色全要素生產率的提升離不開技術創新水平的提高。各個省份應高度重視技術創新，一是加強開發和推廣節能降耗技術，降低行業企業的綜合能耗水平。二是要制定低碳技術創新發展戰略，鼓勵低碳技術的研發和應用，建立低碳技術創新和共享平臺，提升企業在低碳技術創新方面的競爭力。