光學視角下的線段和最值問題解決策略研究

葛小東 丁永愿 馮潤華

課題信息：本文系安徽省合肥市教育科學研究一般課題“初中數學幾何思維可視化教學實踐研究”（課題編號：HJG22055）的研究成果之一.

摘要：線段和的最值問題是初中數學的難點，為降低難度，許多師生按動點軌跡、式子類型等將該問題分為不同種類，這樣使得問題的研究變得零散，運用物理中的費馬原理和折射定律可使得該類型問題的解決具有統一性.

關鍵詞：物理光學;最值問題;跨學科

1 問題提出

線段和的最值問題可以分為以下幾類：將軍飲馬系列，胡不歸系列，阿氏圓系列，費馬點系列等.這些問題主要考查三角函數、相似三角形、兩點之間線段最短、垂線段最短等知識，滲透了對稱、旋轉、平移等圖形變化，是初中幾何問題中的難點.這幾類問題的解答帶有一定的特殊性，當問題推廣到更一般的情況時又該如何解決呢？

問題? 如圖1，求mPA+nPB的最小值，其中m≠n，且m與n均為正常數.

2 問題解析

該問題可看作加權將軍飲馬問題，以學生目前掌握的最值模型是無法解決的.要解決這類問題，我們先了解光的兩大原理.

費馬原理：光在介質中傳播總是選擇耗時最少的路徑.該原理也被稱為“最小時間原理”.

折射定律：如圖2，當光線從介質1中的點M照射到介質Ⅱ中的點N時，sin isin r=V1V2（i，r分別指入射角和折射角，V1，V2分別為光在入射介質與折射介質中的速度）.

根據費馬原理和折射定律，可得當sin isin r=V1V2時，t=OMV1+ONV2有最小值.

如圖3，作點B關于直線l的對稱點B′，mPA+nPB=mPA+nPB′=PA1m+PB′1n，根據上述光學知識，在直線l上確定點P，使得sin αsin β=1m1n=nm，即當msin α=nsin β時，mPA+nPB有最小值.

結論1：如圖3，動點P在直線l上運動時，在直線外有兩定點A，B，過點P作直線l的垂線，當msin α=nsin β時，mPA+nPB有最小值.

特別指出，當α=β時，圖3就是將軍飲馬模型；當α=90°時，圖3就是胡不歸模型.

3 推廣論證

下面將結論1進行推廣，將動點P的軌跡從直線推廣至圓.

結論2：如圖4，當動點P在圓O上運動時，在圓外有兩定點A，B，作射線OP，可得當msin α=nsin β時，mPA+nPB有最小值.

下面將該結論繼續推廣至加權費馬點問題：

在△ABC內找一點P，使得mPA+nPB+kPC最小.（這里m，n，k均為正常數.）

該問題可以通過旋轉、相似來解決，這里方法不再展示.下面主要介紹運用結論2解決該問題的方法.

由于mPA+nPB+kPC=mPA+nmPB+km＼5PC，[JP3]因此該問題可看作PA的長度固定，研究nmPB+kmPC的最小值.如圖5，以A為圓心，PA為半徑作弧，則根據結論2可得，當nk=sin ∠CPDsin ∠BPD時，nmPB+kmPC有最小值.

同理，mPA+nPB+kPC=nmnPA+PB+knPC，可看作PB的長度固定，研究mnPA+knPC的最小值，如圖6，根據結論2可得，當mk=sin ∠EPCsin ∠APE時，mnPA+knPC有最小值，即當sin ∠EPC∶sin ∠CPD∶sin ∠BPD=m∶n∶k時，mPA+nPB+kPC有最小值.

結論3：[JP3]如圖7，在△ABC內存在一點P使得sin ∠BPC∶sin ∠APC∶sin ∠APB=m∶n∶k，則mPA+nPB+kPC有最小值.（其中m，n，k均為正常數.）

至此，初中常見的線段和的最值問題均運用光學定律完成證明.

4 結論的應用

例1? 求y=2（x－1）2+4+（x－8）2+9的最小值.

解析：設P（x，0），A（1，－2），B（8，3），則y=2（x－1）2+4+（x－8）2+9=2PA

+PB=PA0.5+PB1，如圖8.由結論1可得，當sin αsin β=0.51，即sin β=2sin α，亦即PNPB=2PMPN時，2PA+PB有最小值.

由8－x（8－x）2+9=2（x－1）（x－1）2+4，解得x=2，即當x=2時，2PA+PB的最小值為55.

故所求的最小值為55.

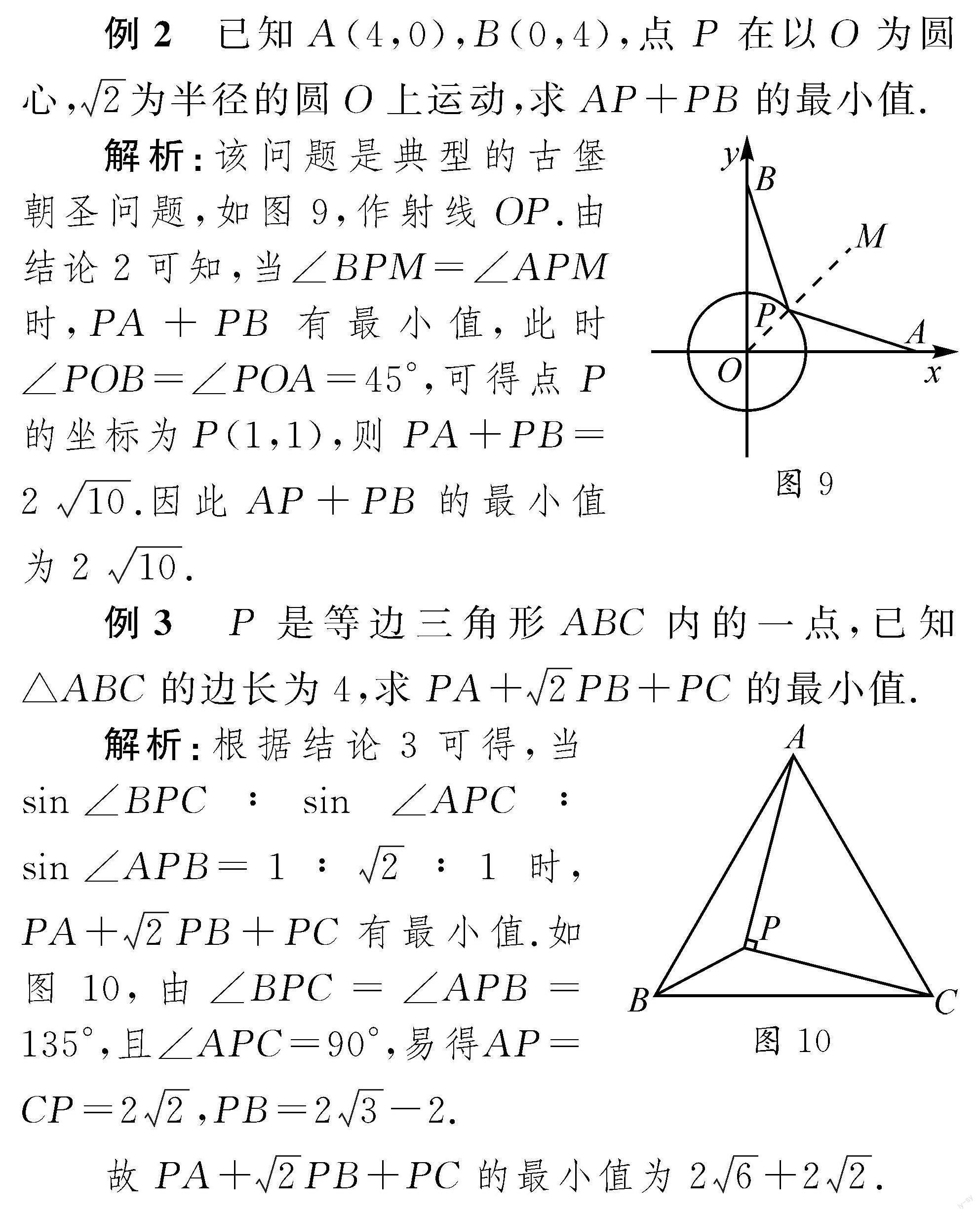
例2? 已知A（4，0），B（0，4），點P在以O為圓心，2為半徑的圓O上運動，求AP+PB的最小值.

解析：該問題是典型的古堡朝圣問題，如圖9，作射線OP.由結論2可知，當∠BPM=∠APM時，PA+PB有最小值，此時∠POB=∠POA=45°，可得點P的坐標為

P（1，1），則PA+PB=210.因此AP+PB的最小值為210.

例3? P是等邊三角形ABC內的一點，已知△ABC的邊長為4，求PA+2PB+PC的最小值.

解析：根據結論3可得，當sin ∠BPC∶sin ∠APC∶sin ∠APB=1∶2∶1時，PA+2PB+PC有最小值.如圖10，由∠BPC=

∠APB=135°，且∠APC=90°，易得AP=CP=22，PB=23－2.

故PA+2PB+PC的最小值為26+22.

5 結語

5.1 跨學科提高學生對知識的理解

本文中提到的折射定律嚴格意義上來說是以費馬原理為依據，運用求導等數學方法論證得來的，但對于初中生來說，求導論證顯然是超綱且困難的，但是將物理結論運用到數學解題中，使得學生對線段和最值的系列問題有了整體的認識.從數學和物理學的角度來說，物理離開了數學幾乎寸步難行，而有時候將數學問題轉化為物理情景賦予物理意義可輕松解決［1］. 線段和的最值問題也可以運用位能最小原理解決，線段比值問題可以運用杠桿原理解決，等等.跨學科促使學生建立學科間的聯系，幫助學生把所學知識融會貫通，形成對知識的整體性和系統性的認知.提高學生的學習興趣， 培養學生的創新意識和綜合能力.

5.2 跨學科促進教師專業發展

在新課標的理念下，教師不能僅僅專注于數學知識的教學和研究，也要加強對數學學科交叉處綜合性較強的知識的理解.跨學科教學可以促進教師不斷去學習新的知識和新的教學技能，且能促進學科之間的交流和碰撞，拓展教師的教學視野，促進教師自身的專業發展和綜合素質的不斷提高.

參考文獻：

［1］鄒生書.一個幾何最值的物理證法及應用［J］.中學數學雜志，2010（3）：35-37.