二維連續型隨機變量函數的獨立性探討

丁尚文, 寧榮健

(1. 合肥工業大學 宣城校區基礎部,安徽 宣城 242000; 2. 合肥工業大學 數學學院,合肥 230601)

0 引 言

對于二維隨機變量(X,Y),X和Y之間的內在聯系是人們關注的問題之一.目前在大多教材中,只介紹了X和Y的獨立性以及相關性等問題,由此不能完全地反映X和Y之間的內在聯系.目前,二維隨機變量(X,Y)函數的獨立性研究比較少,也只是在個別例題中出現驗證某二維連續型隨機變量(X,Y)函數的獨立性,并沒有一般性的結論,因此本文將對二維連續型隨機變量函數(X,Y)函數的獨立性作一點探討.目的是進一步豐富和完善相關教學內容,為教師培養學生創新意識和能力提供素材.

設二維隨機變量(X,Y)的密度函數為

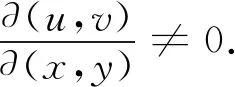
1 主要結論

為討論問題需要,先由《概率論與數理統計》教材[1]中定理3.7.4和文獻[2]中定理2得下列兩個引理.

引理1設二維隨機變量(X,Y)的密度函數為

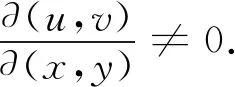
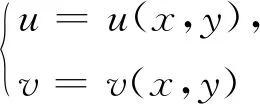
引理2二維隨機變量(X,Y)的密度函數為

其中D為單連通區域,f1(x,y)>0,則X和Y相互獨立的充要條件為D為正矩形區域,且f1(x,y)是可變量分離的.

引理2中,“f1(x,y)是可變量分離的”是指存在一元函數g(x)和h(y),使得f1(x,y)=g1(x)h(y).

由上述兩個引理即得

定理1在引理1中,若Duv為單連通區域,則U和V相互獨立的充要條件為Duv為正矩形區域,且g(u,v)是可變量分離的.

由定理1不難發現以下兩個問題:

一般而言,這并非易事,可根據區域D的特征采取一些變換.比如,如果D是矩形(未必是正矩形),可采取平移變換和旋轉變換將其變為正矩形;如果D是圓形區域,可采用平移變換和極坐標變換將其變為……