高等數學視角下的弧微分公式推導及曲率公式適用條件

強 靜, 邵 虎, 張雙圣

(1.中國礦業大學 數學學院, 江蘇 徐州 221116; 2.徐州工程學院 環境工程學院, 江蘇 徐州 221018)

0 引 言

國內大多數《高等數學》(《微積分》)教材[1-3]在曲率一節中,首先引入弧微分,然后才給出曲率的定義,最后運用弧微分公式推導曲率公式.開篇引入弧微分,略顯突兀,而且在證明弧微分公式時直接使用了“弧長和弦長的比值極限為1”這個假設,證明過程不嚴謹,學生對此常常感到疑惑.

目前,一些研究《高等數學》的學者試圖運用微分理論證明弧微分公式,提出了一些有趣的方法[4-5],但這些方法有不足之處.比如,文獻[4]構造了一個不等式,運用夾逼準則證明弧微分公式,雖然弦長確實小于弧長,但是弧長未必小于文獻[4]中所給兩條線段的和,證明過程出現了疏漏;文獻[5]運用單調有界數列必有極限定理,僅證明了光滑曲線弧在一種分割方式下內接折線長度的極限存在,就認為光滑曲線弧是可求長的,據此又證明了弧微分公式,這種證明過程顯然也有漏洞.另外,《數學分析》[6]中運用積分理論,證明了光滑曲線弧(曲線方程為參數方程)是可求長的,從而得到了弧微分公式,但該證明方法比較繁瑣,其中涉及到一致連續的性質的使用,對于非數學專業學生來說難度較大,不易理解.

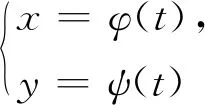
為了解決上述問題,本文首先引出曲率的定義,并給出一種新的曲率的定義形式;在高等數學知識體系內給出一種嚴謹證明弧微分公式的方法;針對上述四種不同形式的……