基于理解的初中數學逆向教學設計

摘 要：數學教學需要在“以學生發展為本”和“以學定教”的指導下進行，以促進學生的全面發展和深度理解.因此，本文采取基于理解的逆向教學設計模式，以《圓和扇形》單元為案例，將明確教學目標、選定評估證據和設計教學活動這三個階段相互關聯，構成一個理解為先的循環教學，提高課堂教學的有效性.

關鍵詞：初中數學；理解；逆向教學設計

中圖分類號：G632 文獻標識碼：A 文章編號：1008-0333（2023）29-0008-03

收稿日期：2023-07-15

作者簡介：王生義（1975.12-），男，本科，中學一級教師，從事初中數學教學研究.

逆向教學設計以理解為目的，通過從學習目標和關鍵理解要點開始，選擇合適的評估證據并設計學習體驗和活動，幫助學生深入理解知識^[1].本文以人教版七年級上冊第三章《圓和扇形》單元為例，將基于理解的逆向教學設計的三個階段相互關聯，構成一個循環的教學過程.這種教學方法注重學生的主動學習和深層次的理解，培養學生的批判性思維和問題解決能力，從而提高學習的質量和效果.

1 基于理解的逆向教學設計

基于理解的逆向教學設計這個觀點首次由威金斯和麥克泰格在《追求理解的教學設計》這本書提出^[2].該教學設計顛覆了傳統的教學方式，以學生理解為先，教師在開始新的學習周期時，需要明確學習結果并確定評估證據，然后設計學習體驗和教學活動，并通過評估證據來檢驗學生的學習成果.它強調學生可以理解哪些知識、學習到什么知識、可以實現怎樣的學習目標、怎樣的方式可以較好地實現預期的目標，從而培養學生的自主學習和問題解決能力^[3].具體分為以下三階段.

1.1 明確教學目標

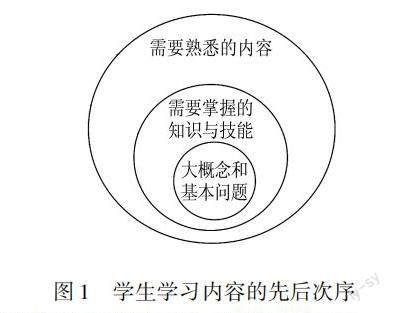
教師需要明確期望學生在學習過程中達到的目標和預期結果，這可以是特定的知識點、技能或能力.明確的學習結果有助于為學生提供明確的學習方向和目標，同時也可以更好地調整和個性化教學，并為后續的評估和教學活動提供指導.當然，這個學習結果需要先了解學生的學習情況，考慮學生的背景、興趣、學習風格和能力水平，確保學習結果與學生的需求和發展階段相匹配，進而確定學生學習內容的先后次序如下圖1所示.

1.2 確定評估學生的證據，即教學評估

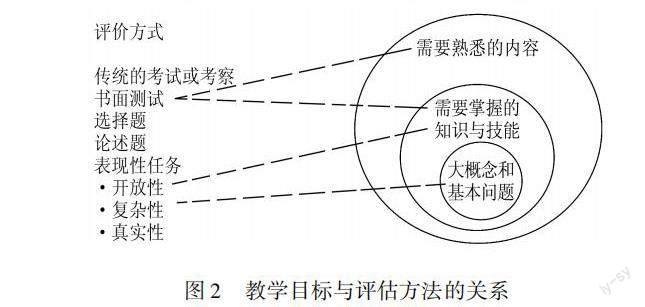
在這個階段，教師需要確定合適的評估方式和評估證據，以判斷學生是否達到了預期的學習結果.評估證據可以是學生的作品、項目成果、考試成績、口頭表達等，確保評價方式與學習目標的要求相匹配如圖2為兩者的關系，并考慮學生的多樣性和不同的學習方式，保證評價標準具有可衡量性和可操作性，能為學生提供有意義的指導.同時，選擇合適的評估方式和證據可以幫助教師準確地評估學生的學習成果，并為教學提供反饋和調整的依據.

1.3 設計教學活動和學習活動

教師需要設計學生的學習體驗和授課活動，以促進學生達到預期的學習結果.通過選擇適當的教學策略、準備多樣化的學習資源、設計有挑戰性的學習任務、創造互動與合作的學習環境，如小組討論、實踐活動、案例研究等，并關注個性化的學習需求，以激發學生的學習動力，培養他們的批判性思維和創造性解決問題的能力.這樣的設計將使學習變得有趣、有意義，并幫助學生在學習中取得更好的成果.

2 基于理解的逆向教學設計案例

2.1 階段一

2.1.1 課程單元教學目標

（1）準確地定義和描述圓的基本概念，以及解釋圓的性質.

（2）正確地計算扇形的面積和弧長，并能夠合理地應用所學知識解決實際問題.

（3）清晰地表達數學思想和解題過程，并用準確的數學語言和符號論證和計算.

2.1.2 學生的學習標準

（1）定義和描述圓的圓心、半徑、直徑、弧長等基本概念.例如，學生能夠正確定義圓心為位于圓內，到圓上任意一點距離相等的點.

（2）說明圓的圓心角等于弧度角、同弧度的圓心角相等、圓內角和等于180度等性質.例如，學生能夠理解圓心角是以圓心為頂點的角，其度數等于對應的弧度.

（3）計算扇形的面積和弧長，理解扇形面積和弧長的計算公式的推導過程.例如，學生能夠應用面積計算公式S=1/2r²θ以及弧長計算公式L=rθ進行計算.

（4）將所學知識應用于解決實際問題，如計算圓形花壇的面積、扇形的面積等.例如，學生能夠應用所學知識計算一個半徑為5 cm的扇形所覆蓋的面積.

（5）應用圓與扇形相關的公式對不規則形狀或者組合圖形的周長和面積進行計算.

2.1.3 實際應用

（1）應用所學的圓和扇形的知識解決實際問題.例如，學生可以計算圓形花壇的面積，以確定需要的土壤和植物的數量.

（2）應用扇形面積和弧長的計算方法，來解決與地理、建筑等領域相關的問題.例如，學生可以計算一個舞臺上的扇形區域的面積，以決定舞臺上的舞蹈表演區域.

（3）將圓和扇形的概念應用于日常生活中的實際情境.例如，在選購蛋糕時，學生可以計算扇形蛋糕的面積和價格，以做出更明智的選擇.

2.2 階段二

在人教版《圓和扇形》單元中，為了評估學生對于所學知識的掌握程度，可以采用以下合適的評估證據：

2.2.1 筆試評估

（1）設計選擇題和填空題，考查學生對圓與扇形基本概念、性質和計算公式的理解和應用.例如，要求學生選擇正確的定義或性質，填寫圓的半徑或弧長的計算結果等.

（2）設計解答題，要求學生回答文字題目，解決與圓與扇形相關的問題.例如，要求學生計算不規則形狀或組合圖形的周長和面積，并給出解題步驟和思路.

2.2.2 實際問題解決評估

（1）給學生一些實際情境，要求他們運用圓與扇形的知識解決問題，例如計算花壇的面積、舞臺上扇形區域的面積等.

（2）要求學生給出解決問題的全面解答，包括問題的分析和解決思路，并通過計算和推理得出結論.

2.2.3 實際操作評估

（1）通過測量、模擬實驗等，進行圓與扇形面積、周長以及相關公式的推導進行驗證.

（2）組織學生進行小組或個人項目作業，要求他們設計和繪制一個具有特定要求的不規則形狀或組合圖形，計算其周長和面積，請說明設計意圖.

（3）要求學生書面報告項目作業的過程和結果，并附上必要的圖表和計算步驟.

2.3 階段三

以下為有利于學生理解的具體活動.

2.3.1 演示與探究

（1）首先使用實物或模型，展示圓的形狀和特性，例如使用井蓋、圓盤、圓規等，引導學生觀察和描述圓的性質.

（2）設計探究活動，讓學生自己測量和驗證圓心角、弧長等與圓相關的性質.例如，組織學生測量不同角度的圓心角，并觀察角度與弧長的關系.

2.3.2 問題解決與實踐

（1）提供一系列與圓和扇形相關的問題，鼓勵學生運用所學知識解決.例如，給學生幾個不規則形狀的圖形，要求他們計算每個圖形的面積和周長.

（2）設計實踐活動，讓學生在實際場景中應用圓與扇形的知識.例如，帶學生到校園中測量不同樹木的樹冠直徑，并計算樹冠的面積.

2.3.3 合作學習與討論

（1）安排學生成小組，讓他們共同討論和解決與圓與扇形單元相關的問題.通過討論，促進學生思維的碰撞和深入理解.

（2）設計小組項目，要求學生合作設計一個花壇或場地的規劃，包括圓形和扇形區域的設計和計算.

2.3.4 利用技術工具

引入相關的數學教學軟件或在線工具，讓學生通過模擬和計算來探索圓與扇形單元的知識.例如，使用幾何繪圖軟件進行不規則圖形的繪制和計算.

2.3.5 視頻和多媒體資源

利用相關的視頻和多媒體資源，呈現圓與扇形單元的概念和應用.通過視聽的方式，幫助學生更直觀地理解和記憶相關知識.

3 小結與啟示

基于理解的逆向教學設計在初中數學教學中，有效提升學生的理解和應用能力.通過明確學習目標和理解要點，引導學生參與觀察、探索、實踐和問題解決，促進知識建構，并整合數學和實際情境，設計實用的活動培養深度理解，創造多樣化的學習體驗，以激發學生學習興趣.同時，及時反饋和評估，鞏固知識和調整教學策略.進而，做到以學促教、以理解為先的教學和學習，促進深層次的學習，為學生未來的學習打下堅實的基礎.

參考文獻：

[1] 夏君.基于理解為先的逆向教學設計的鄉鎮初中學校校本研修行動研究[J].教育參考，2023（02）：36-42.

[2] 格蘭特·威金斯，杰伊·麥克泰格.追求理解的教學設計（第二版）[M].上海：華東師范大學出版社，2017.

[3] 呂龍.基于理解的初中數學逆向教學設計：以“圓和扇形”單元為例[J].上海中學數學，2021（04）：40-42.

[責任編輯：李 璟]