黃偉東

摘 要： 為響應國家“雙減”政策號召，筆者結合省數學學科教學基本要求，調查研究小學數學課堂核心問題設計現狀，并進行歸因分析，從路徑探索、策略實施兩方面闡述對小學數學課堂核心問題設計的干預，以求學生在減負不減質中深度思考，提升數學思維.

關鍵詞： 核心問題；現狀歸因；設計路徑；有效策略

南京大學鄭毓信教授指出，“微觀意義上的核心問題”是指就一節課或相關的幾節課提煉出相應的“核心問題”.“宏觀意義上的核心問題”能通過整體性分析弄清內在脈絡，并凸顯其中的關鍵，從而真正起到提綱挈領的作用.

本文關注的課堂核心問題是指教師基于對教材的深度理解和對學情的精準把握，在課堂上精心設計適合學生探究的、提升學生高階思維的問題.核心問題一般具有一定張力和彈性的特點，能使學生的學習聚焦并主動探究、層層深入.

1 ?研究背景及現狀

1.1 ?減負提質增效率：響應國家雙減政策的號召

2021年7月，中共中央辦公廳、國務院辦公廳印發了《關于進一步減輕義務教育階段學生作業負擔和校外培訓負擔的意見》，其中提出“優化教學方式，提升課堂教學質量”“提高學生學習效率，促進學生全面發展”等意見.該文件的發布為“提高教師核心問題設計能力”的提出奠定了基調，從國家層面錨定了戰略高度.

1.2 ?賦能促思蘊素養：落實省市學科教學的要求

2021年9月印發的《浙江省小學數學學科教學基本要求（2021版）》中第8條指出：“教學環節的構建和情境的創設都須注重數學問題的設計.問題的有效設計是推進課堂教學進程的關鍵.”結合××市教科研院發布的教科研指導意見，筆者進行了小學數學核心問題設計的研究，為構建素養課堂，從省市層面篤定了研究方向.

1.3 ?區域調研顯問題：聚焦核心問題設計的困惑

筆者通過對區域內103位教師進行調查問卷，聚焦小學數學課堂核心問題設計的現狀并嘗試歸因，發現教師存在以下困惑：

1.3.1 問題缺乏深度，無法立足知識本源

教材的認知是問題篩選的前提，但調查中53.4 % 的教師提問時過多關注教學內容，缺乏對教材的深入解讀和對核心問題的提煉.

1.3.2 問題缺乏力度，無法依托學習路徑

活動的開展是問題聯結的載體，但調查中69.9 % 的教師在教學時不擅長基于學習路徑以問題鏈助推問題的解決.

1.3.3 問題缺乏梯度，無法彰顯彈性分層

素材的選取是問題發生的支架，但調查中87.4 % 的教師不擅長提供多元素材驅動自主建構，難以滿足不同學生的探究需求.

1.3.4 問題缺乏廣度，無法滲透數學思想

思維的發展是核心問題設計的導向，但調查中32.0%的教師的問題設計缺乏思維空間，無法融入數學思想.因此，筆者希望在小學數學課堂核心問題設計的路徑及策略上干預，以期提高教師核心問題的設計能力，并在課堂教學實踐中發展學生的數學核心素養.

2 ?小學數學課堂核心問題設計的基本路徑

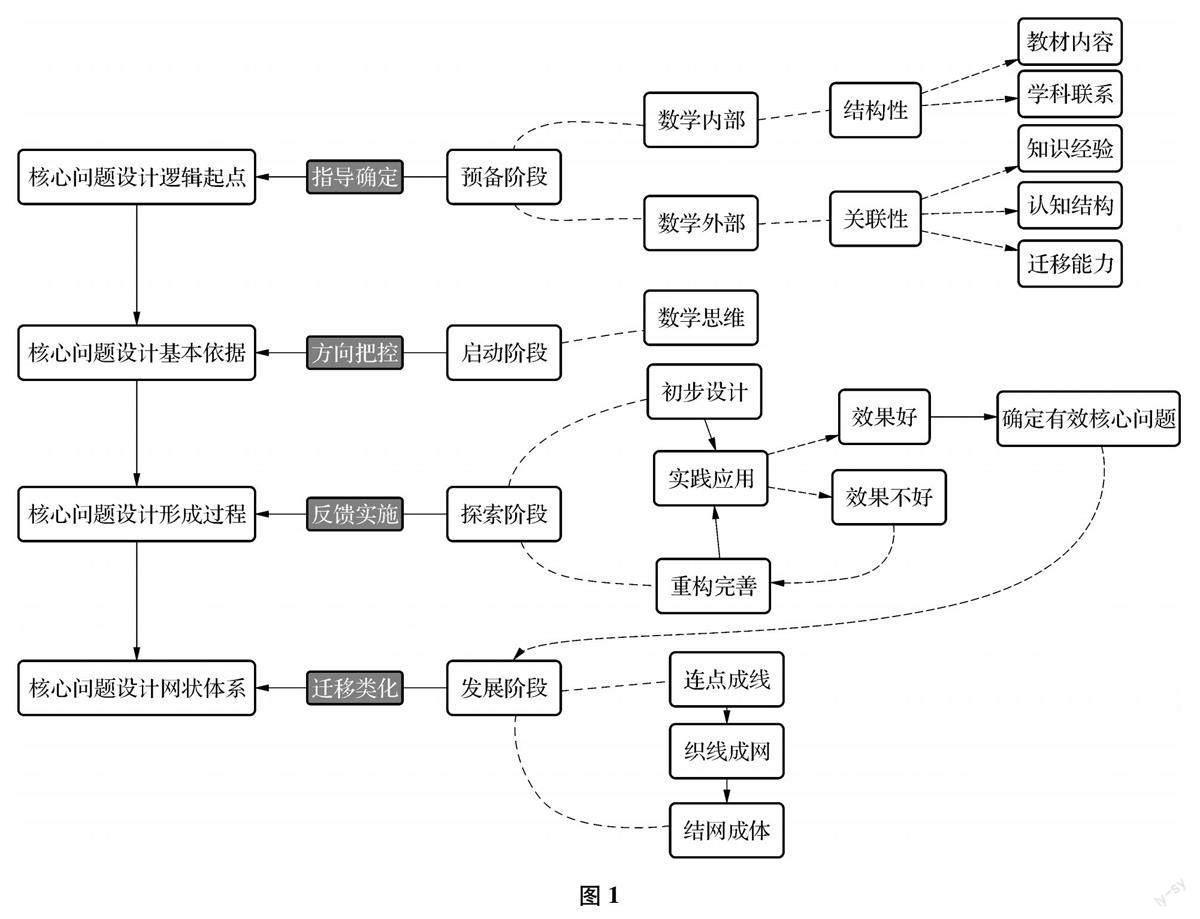
基于小學數學課堂核心問題的現狀調查及歸因分析，筆者查閱資料并結合自身教學經驗嘗試以邏輯起點、基本依據、形成過程以及網狀體系為路徑展開設計小學數學課堂核心問題（如圖1）.

2.1 ?確立核心問題設計的邏輯起點

核心問題設計的邏輯起點包括結構性的數學內部和關聯性的數學外部.數學外部包括學生已有知識經驗、認知結構以及不同年齡階段的學生的心理特點等，數學內部則包括數學教材中的上位知識、顯性知識以及隱性知識.

2.2 ?明晰核心問題設計的基本依據

問題是課堂的核心，是啟發和引導學生探究的有效載體，但教師的問題往往過于直接，問題與問題之間的跨度比較小，限制了學生的數學思考.因此，筆者以發展學生的數學思維為依據來設計核心問題，以存在邏輯關系的問題鏈啟發學生在師生互動的過程中提出本原性問題，從而將教材、教師以及學生的問題整合為課堂學習的核心問題.利用核心問題的牽引力以及問題鏈的驅動力，提高教師課堂教學的有效力.

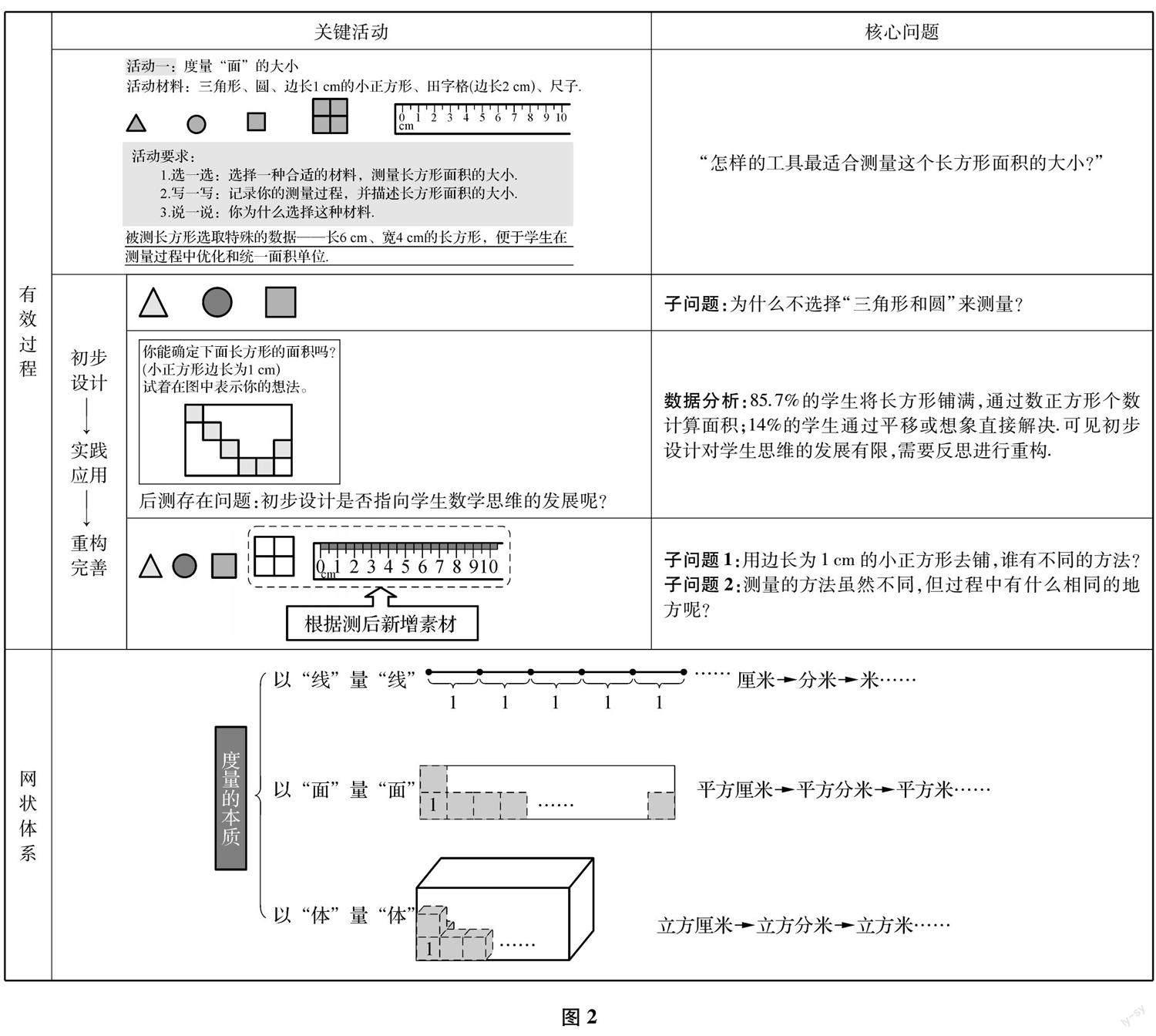
2.3 ?形成核心問題設計的有效過程

核心問題設計的有效過程通常需要經歷“初步設計——實踐應用——重構完善”三個過程（如圖2）.確定核心問題后，在不斷的實踐反饋與跟蹤調整中，對活動材料進行重構完善，新增“田字格”和“尺子”，旨在擴充核心問題的思維空間，使學生經歷從“田字型”到“日字型”再到“口字型”的逐步調整過程，積累將“大單位”細分為“小單位”的活動經驗，從而理解統一單位的必要性.由于學生的認知水平存在差異性，為了讓不同思維層次的學生在同一教學環境中獲得最高效的收獲，唯有依托核心問題的引領，以多元素材的選擇，實踐學為中心的教育本真.

2.4 ?建構核心問題設計的網狀體系

有效的課堂核心問題并不只是針對單一一節課的設計，而應對同類型的其他教學內容的核心問題設計也有啟發性和可操作性.比如前文中提到的以“面”量“面”的數學內容，筆者在設計核心問題時都會與之前學習的以“線”量“線”以及后續的以“體”量“體”教學聯系起來，其設計核心問題的路徑也是一脈相承的.筆者以一節課核心問題的有效設計關聯一類課，做好連點成線、織線成網，結網成體（如圖2）.

3 ?小學數學課堂核心問題設計的有效策略

3.1 ?以教材結構為本，單元視角整合核心問題

案例1 ??從《三角形》單元整體角度確立核心問題總方向、總思路及總框架.

3.1.1 整體解讀教材，明晰核心問題總方向

四年級學生對平面圖形的認識經驗已較為豐富，也形成了一定的圖形探究能力，尤其是四年級上冊（人教版）中角和四邊形的學習，給學生積累了學習三角形的活動經驗，學生能將學習四邊形的學習經驗遷移到三角形的認識中.因此，本單元的學習適合整合，通過對教材的整體解讀，確定以“邊”和“角”兩大元素整合教學內容，明晰核心問題的總方向.

3.1.2 整體創設單元，形成核心問題總框架

單元視角下，筆者嘗試創設《三角形》單元整體教學結構，并形成各部分應有的課堂核心問題總框架以及相應的子問題.比如在“邊”的教學中，利用三根小棒的拼擺活動分別解決：① 搭一個三角形需要幾根小棒？② 三根小棒一定能拼成三角形嗎？③ 符合條件的三根小棒能擺出不同形狀的三角形嗎？④ 選擇不同長度的小棒搭不同類的三角形.這四個目標指向明晰的子問題，從而完成對三角形“定義——關系——特性——分類”的整體認識，豐富概念的內涵和外延.

3.1.3 整體把控學情，理清核心問題總思路

在充分研讀教材的基礎上，對學生的學情進行把控，得到學生對該單元知識的困惑以及已有的經驗水平，并及時進行精準的分析和理解，從而確定核心問題的總思路.教師只有了解學生在三角形認識過程中的思維障礙點和知識生長點，才能對癥下藥地設計有層次、有彈性、有思維空間的核心問題，統籌安排教學任務，開展有針對性的學習活動，讓學生的思維能力發展都落在最近發展區中.

3.2 ?以重難關鍵為點，深度關聯形成問題鏈條

小學數學課堂教學應在教學的重、難關鍵之處設計核心問題.教師應根據教學目標對核心問題進行分解，創設有梯度、有關聯的子問題，并以核心問題的牽引力激發問題鏈的驅動力，盤活學生已有的認知力，導引學生后續的學習力，建構結構化的知識網.

3.3 ?以活動素材為支，多元拓寬培養提問意識

核心問題的落實離不開活動素材的設置，單一的素材容易讓學生走向“程序員”的操作誤區，不利于學生的思維發展.因此，教師要精心設計多元的活動素材，引導學生的思維不斷碰撞，鼓勵學生發現和提出問題.

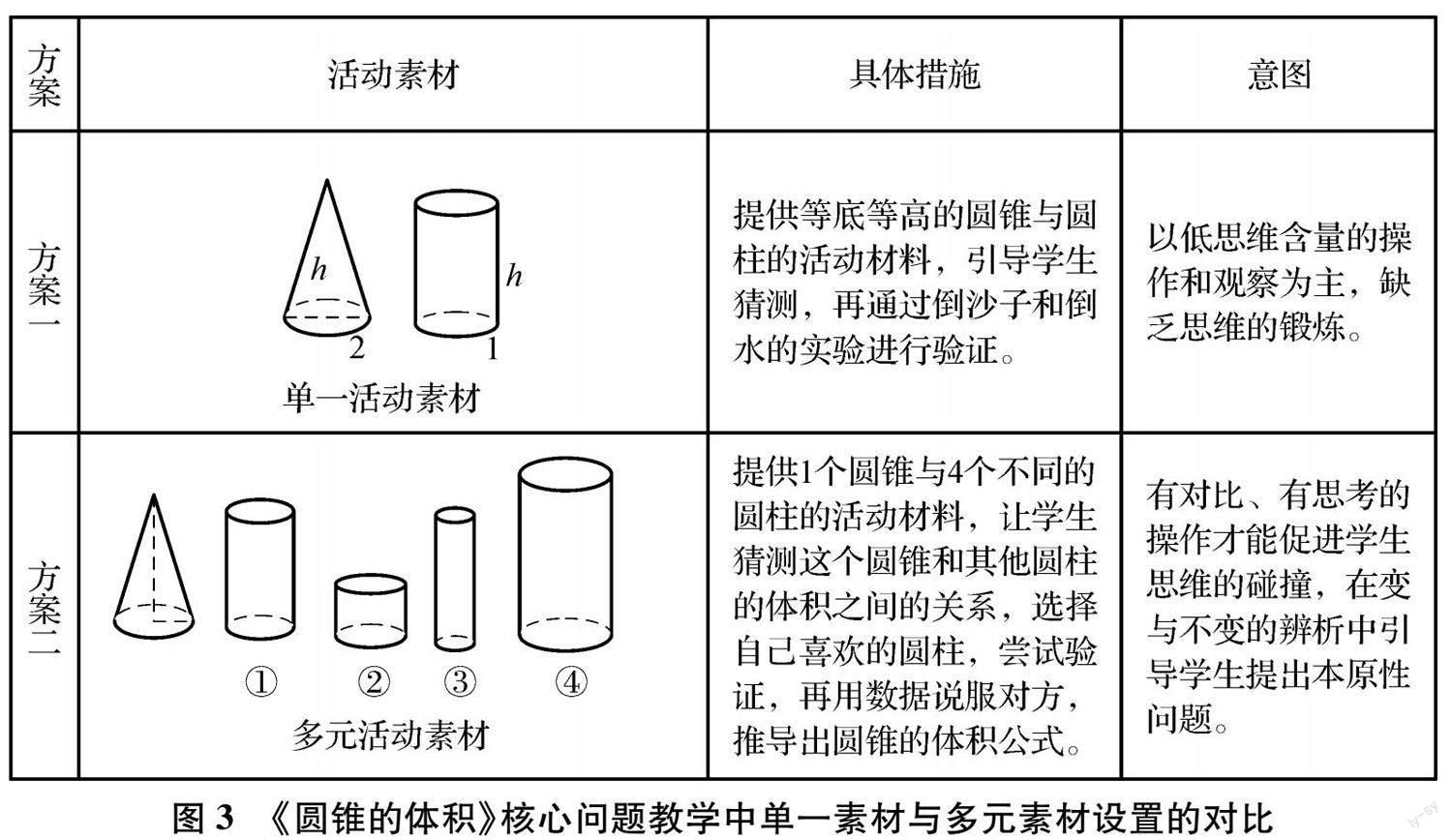
案例2 ??《圓錐的體積》差異比較.

單一的活動素材和多元活動素材的課堂教學片段如圖3所示，以求凸顯活動素材多元化的重要性.雖然都以活動素材為支架進行操作實驗，得出結論，但［方案一］僅提供等底等高的圓錐與圓柱，限制了學生思維的發散， 而［方案二］避免了學生忙于操作實驗而淡化思考和分析的現象，促使學生在多元素材的對比溝通中主動尋求共性規律，揭開表象，深究其內在聯系.

3.4 ?以數學思想為引，遷移延展深化核心素養

在教材遷移之處設計核心問題，有助于改變教師自身散點狀、割裂式的思維方式，養成一種強調方法更強調思想的內在遷移式的思考習慣.而學生對新舊知識的充分聯結、遷移和延展能讓其數學核心素養達成深化.

案例3 ??《商是兩位數的除法》教學以核心問題推進進程.

以核心問題“612÷18豎式有幾層”推進教學進程，以“第一層分什么？”“第二層分什么？”“商是幾位數，寫在什么位上？”三個子問題盤活學生已有的認知力，導引學生后續的學習力，讓學生將“位值的概念”和“豎式的層數”有效地聯系起來，結構化地理解除法豎式的模型，實現學生思維從低階向高階的發展，從而實現“一層豎式”向“二層豎式”的思維進階，“二層豎式”向“多層豎式”的思維迭代過程（如圖4）.

“雙減”是一項政策，更是一種行動，我們響應“雙減”號召，以學科教學基本要求為引，共聚“核心問題設計”研究，思考路徑，探究策略，減中有增，增中有提，為減負，為提質，更為共進.讓我們致力于教與學現狀的改善，以學生終身成長為目標，讓教育返璞歸真，讓“雙減”落地生根.

參考文獻：

［1］ 鄭毓信.中國數學教育的“問題特色”［J］.數學教育學報，2018，27（1）：1 7.

［2］ 劉媛.“核心問題”引領下的小學數學課堂教學策略研究［D］.南京師范大學：2020.