復合故障狀態下行星齒輪-轉子耦合系統振動響應特性研究*

周博虎,李國彥,2,3*,任昱霖,熊曉燕,2

(1.太原理工大學 機械與運載工程學院,山西 太原 030024;2.太原理工大學 新型傳感器與智能控制教育部重點實驗室,山西 太原 030024;3.電子科技大學 機械與電氣工程學院,四川 成都 611731)

0 引 言

行星齒輪箱是風力發電機組、工程機械等大型復雜機械裝備的核心傳動部件。在齒輪箱的長期服役過程中,齒輪承受著交變載荷的作用,容易出現疲勞裂紋損傷,需準確評估其健康狀況,以免其影響設備整機的安全運行。因此,開展行星齒輪傳動系統早期裂紋故障診斷技術研究具有重要意義[1-2]。

由于振動信號中包含有豐富的設備狀態信息,基于振動分析的行星齒輪裂紋故障診斷技術受到了國內外研究者的廣泛關注。

劉杰等人[3]基于能量法建立了齒根裂紋模型,借此研究了太陽輪齒根裂紋對行星輪系動態特性的影響規律。孟宗等人[4]根據齒輪過渡曲線函數,對完整的齒廓曲線進行了分析,采用勢能法計算了不同裂紋長度下的嚙合剛度,并得出結論,峭度指標能很好地用于區分不同裂紋程度。肖正明等人[5]采用仿真與實驗的對比分析方法,研究了裂紋故障對行星齒輪傳動系統動力學特性的影響,結果發現,裂紋故障會導致系統振動出現調制效應,且故障齒輪箱的振動能量主要集中在高頻段。ZHANG M等人[6]提出了考慮含太陽故障位置信息的運動周期模型,并使用仿真和實驗的方法,闡釋了故障相關邊帶產生的機理。謝福起等人[7]研究了太陽輪雙齒裂紋對系統階次譜成分的影響。

上述研究僅針對單一齒輪結構的振動特性進行了分析。但是,實際上行星齒輪箱內部零件數量眾多,并且會形成復雜的配合關系。其中,轉軸是齒輪系統重要的傳動及支撐零件。由于材質不均勻、加工誤差、不均勻磨損等因素的影響,轉軸的偏心問題難以避免。在轉軸的高速旋轉過程中,偏心質量會產生不平衡激振力,其作為一種外部激勵,會對齒輪系統的振動特性及故障特性產生復雜的影響。

目前,國內外學者對齒輪-轉子耦合系統的動力學特性進行了研究。但是,專門針對行星齒輪-轉子耦合系統故障特性的相關研究較少。

ZHANG H等人[8]建立了一種壓縮機齒輪-轉子動力學模型,并采用該模型,得到了不平衡激勵下系統的加速度頻譜特征。SAXENA A等人[9]建立了含齒根裂紋的齒輪-轉子模型,并借助該模型,研究了裂紋故障對系統的固有頻率和模態的影響規律。HUANGFU Y等人[10]建立了斜齒輪-轉子動力學模型,并根據該模型,研究了陀螺效應和齒輪螺旋角對節點振動位移的影響規律。侯蘭蘭等人[11]研究了傳動軸扭轉剛度比對行星齒輪-轉子系統非線性動力學響應的影響。WANG Q B等人[12]研究了軸承不對中對行星齒輪-轉子系統動態特性的影響。

但是在上述研究中,研究人員均沒有考慮行星齒輪-轉子復合故障狀態。

事實上,行星齒輪-轉子的復合故障信息,除了正常嚙合引起的內部激勵和輪齒損傷引起的故障信息成分以外,還包括受到轉子不平衡引起的外部激勵干擾信息。這些信息傳遞到行星齒輪箱測點位置引起的振動,會導致測點信號復雜,進而使得行星齒輪-轉子系統早期裂紋故障診斷困難。

因此,筆者構建含轉子偏心和齒根裂紋故障的行星齒輪-轉子耦合系統動力學模型,研究復合故障狀態下的系統振動響應特性。

首先,基于節點有限元法,建立行星齒輪-轉子耦合系統的動力學模型,并將含裂紋輪齒嚙合剛度模型和轉子不平衡模型集成到系統動力學模型中;然后,采用數值仿真方法,獲取不同故障狀況下的系統振動響應信號,綜合采用時間歷程、頻譜、軸心軌跡及相軌跡,對系統的故障特性進行分析;最后,開展含裂紋故障的行星齒輪箱故障測試實驗,以驗證齒輪-轉子系統動力學模型的有效性。

筆者綜合挖掘齒輪、轉軸系統振動響應中包含的故障信息,以期為基于振動分析的行星齒輪箱早期裂紋故障診斷提供依據。

1 行星齒輪-轉子系統動力學模型

1.1 行星輪系非線性動力學模型

2K-H行星輪系集中參數動力學模型如圖1所示。

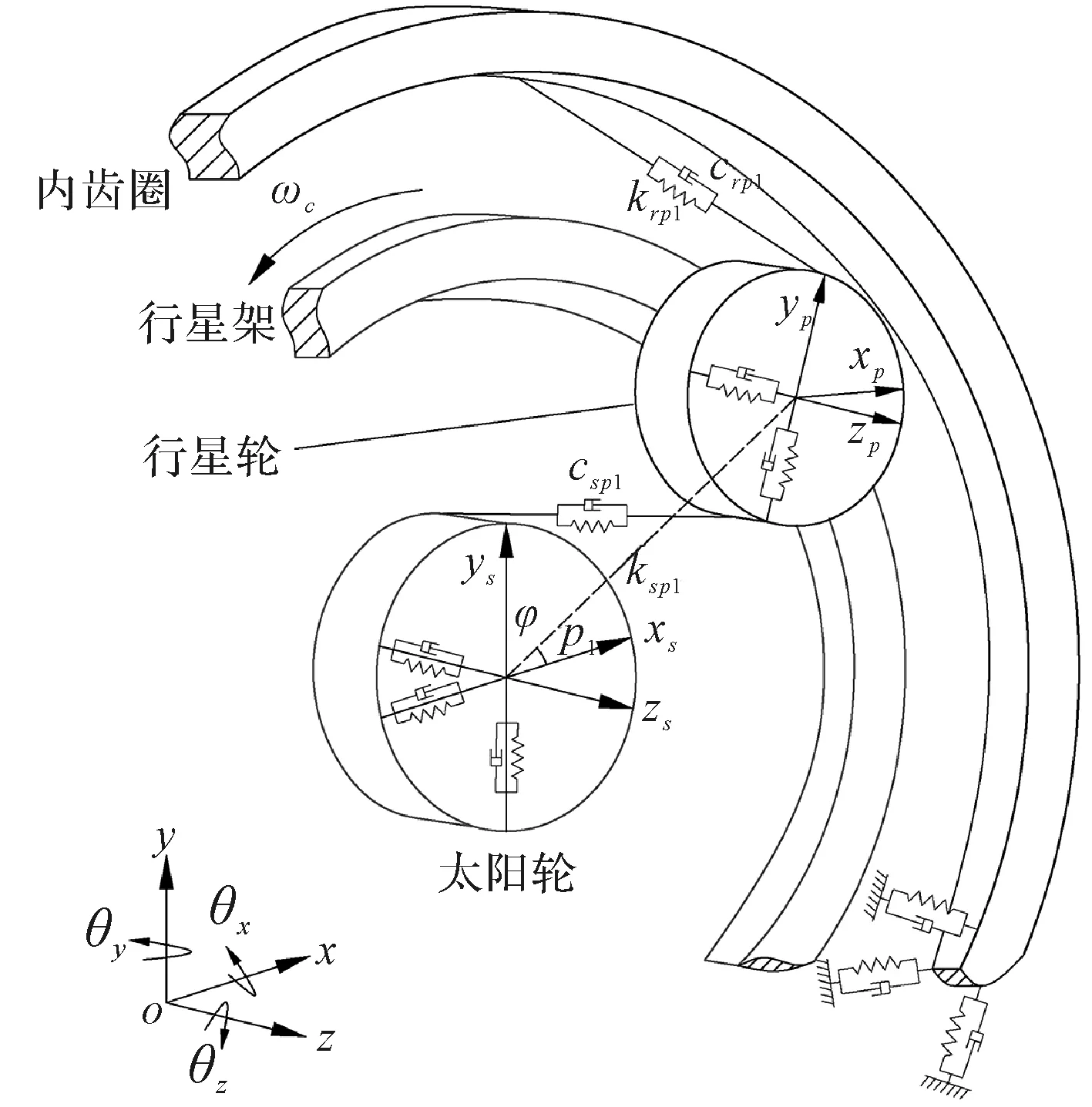
圖1 2K-H行星輪系動力學模型

圖1中,行星齒輪系統的太陽輪作為系統動力的輸入端,行星架作為系統動力的輸出端,而內齒圈固定。

該模型考慮了時變嚙合剛度、支撐剛度、阻尼、陀螺效應等非線性因素。模型中各構件具有6個自由度(分別為:x、y橫向,z軸向,θx、θy擺動和θz扭轉方向的變形)。

各構件質心的廣義坐標為:

qj=[xj,yj,zj,θxj,θyj,θzj]T

(1)

式中:下標j代表太陽輪s、行星輪pi(i=1,2…N,N=3)、齒圈r以及行星架c。

筆者將嚙合副等效為彈簧阻尼結構;設內外嚙合副沿嚙合線方向的相對位移為δspi和δrpi,這里假定各構件逆時針旋轉方向為正,壓縮方向為正。

則有:

δspi=(xpi-xs)cosφspi+(ypi-ys)sinφspi-θzsrbs-θzpirbp

δrpi=(xpi-xr)cosφrpi+(ypi-yr)sinφrpi-θzrrbr+θzpirbp

(2)

行星架與行星輪之間的相對位移為:

δxcpi=xpi-xc+θzcrcsinφpi

δycpi=ypi-yc-θzcrccosφpi

δzcpi=zpi-zc+θycrccosφpi-θxcrcsinφpi

(3)

式中:φspi,φrpi為太陽輪-行星輪、齒圈-行星輪相對嚙合角;φpi為行星輪位置角;α為壓力角;rbj為各齒輪構件基圓半徑;rc為行星架中心到行星輪中心的距離。

其中:φspi=φpi-α;φrpi=φpi+α。

嚙合副間的嚙合力可表示為:

(4)

行星架對行星輪的支撐力可表示為:

(5)

式中:下標m為太陽輪-行星輪嚙合副spi以及齒圈-行星輪嚙合副rpi;km為時變嚙合剛度;cm為嚙合阻尼;kp為行星架對行星輪的支撐剛度;cp為行星架對行星輪的支撐阻尼。

根據牛頓第二定律,筆者推導出各個構件的運動微分方程如下:

1)太陽輪的運動微分方程。其表達式為:

(6)

2)內齒圈的運動微分方程。其表達式為:

(7)

3)行星輪的運動微分方程。其表達式為:

(8)

4)行星架的運動微分方程。其表達式為:

(9)

式中:mj為構件j的質量;Jdj為構件j的直徑轉動慣量;Jpj為構件j的極轉動慣量;kxj,kyj,kzj,kθxj,kθyj為構件j在x,y,z,θx,θy方向上的支撐剛度;cxj,cyj,czj,cθxj,cθyj為構件j在x,y,z,θx,θy方向上的支撐阻尼;kθzr,cθzr為內齒圈在θz方向上的支撐剛度和阻尼;ωc為行星架轉動角速度;ωs為太陽輪轉動角速度;Tin為輸入轉矩;Tout為輸出轉矩。

聯立上述方程,經整理后可得到行星輪系動力學矩陣方程,即:

(10)

式中:Mpg為行星輪系的質量矩陣;KG為陀螺矩陣;Kc為行星輪系的向心剛度矩陣;Km,Kb為嚙合剛度和支撐剛度矩陣;Cm,Cb為嚙合阻尼矩陣和支撐阻尼矩陣;T為系統的輸入輸出轉矩矩陣;G為系統的重力矩陣。

根據文獻[13],筆者取支撐剛度為1×108N/m,取值支撐阻尼為1.5×103N·s/m,則齒輪副間的嚙合阻尼為:

(11)

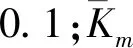
1.2 偏心轉軸系統動力學模型

在考慮行星輪系輸入及輸出軸柔性的基礎上,筆者采用Timoshenko梁單元模型,并基于有限元思想,將軸系沿軸線方向劃分成不同節點,每個節點考慮6個自由度(分別為x、y橫向,z軸向,θx、θy擺動和θz扭轉方向的變形)。

各節點的位移向量可表示為:

qu=[xu,yu,zu,θxu,θyu,θzu]T

(12)

式中:下標u為輸入軸和輸出軸各個節點。

轉子偏心引起的外部激勵可表示為:

Fω=muω2e

(13)

將外部激勵分解到x、y方向上,可分別表示為:

Fωx=muω2ecos(ωt+φ),Fωy=muω2esin(ωt+φ)

(14)

式中:mu為節點u的質量;ω為轉軸轉動角速度;e為偏心距離;φ為偏心初相位。

根據Timoshenko梁理論,可建立考慮陀螺效應影響因素的轉軸動力學矩陣方程[14]:

(15)

式中:Mr為轉子的質量矩陣;Gr為轉子的陀螺矩陣;Kr為剛度矩陣;F為外部激勵矩陣。

其中:在偏心節點處,Fu=[Fωx,Fωy,0,0,0,0]。

1.3 含裂紋齒輪副時變嚙合剛度模型

筆者將建立裂紋損傷參數與時變嚙合剛度間的量化關系,并以內部激勵的形式,將齒根裂紋損傷引入行星輪系動力學模型中;將齒輪簡化為懸臂梁模型,基于能量法推導正常及含裂紋輪齒時變嚙合剛度。

含裂紋太陽輪輪齒及其橫截面如圖2所示[15]。

圖2 含裂紋輪齒橫截面

圖2中,假設裂紋產生于太陽輪齒根位置處,沿著與輪齒中心線呈v=30°的方向擴展(裂紋尺寸用q1表示),則當裂紋擴展到與輪齒中心線相交處(定義裂紋程度為50%),之后,裂紋沿v=-30°方向擴展(裂紋尺寸用q2表示),直到輪齒瞬間斷裂為止。

根據能量法,有4種剛度影響著齒輪綜合嚙合剛度,分別為彎曲剛度kb、剪切剛度ks、軸向壓縮剛度ka和赫茲接觸剛度kh。

當輪齒嚙合處于損傷區域時,輪齒的橫截面會產生變化,導致彎曲剛度和剪切剛度分量發生變化,并進一步影響輪齒的綜合嚙合剛度[15-16]。

損傷橫截面的面積Acx和慣性矩Icx表達式如下:

(16)

裂紋區域的彎曲剛度和剪切剛度的表達式如下:

(17)

式中:W為齒寬;α1為嚙合點對應的嚙合角;d為嚙合點到齒根處的距離;x為嚙合點到齒根的區域內任意一點到齒根圓的距離;h為嚙合點到輪齒中心線的距離;hx為嚙合點到齒根的區域內任意一點到輪齒中心線的距離;hd為受力邊界點到輪齒中心線的距離。

綜上所述,根據單齒對嚙合剛度計算公式,可以得到含裂紋故障的時變嚙合剛度,即:

(18)

在裂紋深度變化情況下,太陽輪-行星輪嚙合副時變嚙合剛度如圖3所示。

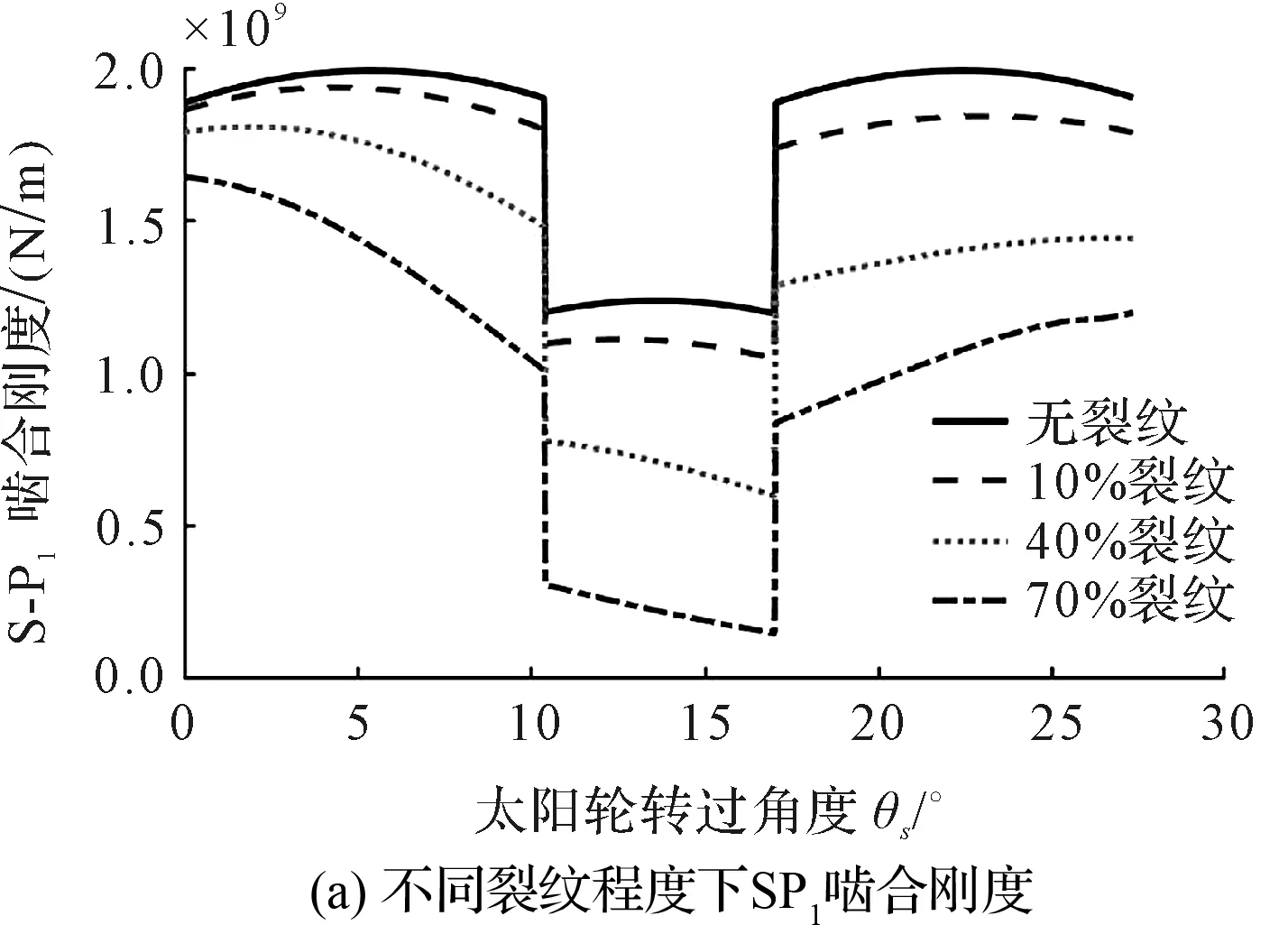
圖3 含裂紋S-P嚙合副嚙合剛度

由圖3(a)可知:在10%、40%和70%裂紋損傷下,相對于正常情況,含裂紋嚙合副的平均嚙合剛度分別下降了5.15%、21.1%和43.9%;

從圖3(b)可知:太陽輪每旋轉一周,含裂紋輪齒以tsc的時間間隔依次與配對行星輪嚙合,導致太陽輪-行星輪嚙合副的剛度值周期性降低,從而引起輪系統沖擊性振動響應。

1.4 模型總裝

行星齒輪-轉子三維模型如圖4所示。

圖4 2K-H行星齒輪傳動系統三維模型

筆者分別采用上述行星輪系和偏心轉軸系統的建模方法,對行星齒輪和轉子進行建模。

在綜合考慮轉軸偏心和齒輪裂紋故障的基礎上,得到行星齒輪-轉子耦合系統動力學模型,如圖5所示。

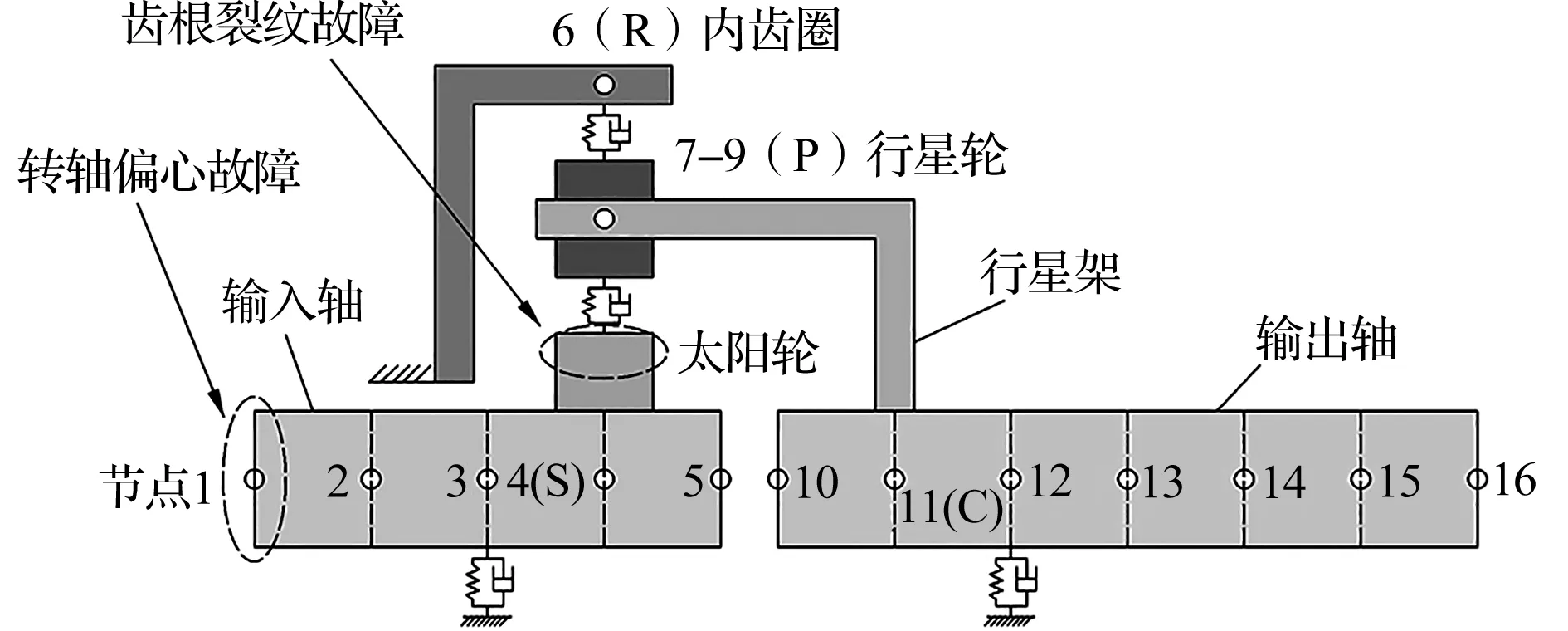
圖5 行星齒輪-轉子復合故障系統動力學模型

圖5中,筆者劃分整個系統為16個節點、96個自由度。其中,節點4為太陽輪,節點6為內齒圈,節點7～9為3個均勻分布的行星輪,節點11為行星架。轉軸偏心設置在輸入軸端節點1處,齒根裂紋故障設置在太陽輪處。

總裝后的整體動力學矩陣方程可表示為:

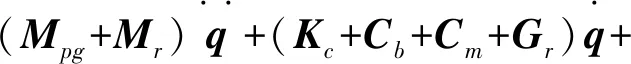
(19)

筆者組裝各節點質量、剛度和阻尼矩陣,可得系統有限元總裝矩陣[17]。

組裝后的系統剛度矩陣如圖6所示。

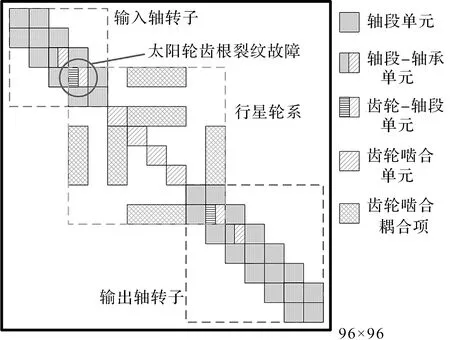
圖6 系統總體剛度矩陣

2 齒輪-轉子系統復合故障振動特性

此處筆者以某工程機械變速箱行星輪系為實例。在輸入轉速1 500 r/min、輸出轉矩100 N·m的工況下,筆者采用Newmark-β數值積分法,對上述動力學模型進行求解,得到不同故障狀態下的系統動力學響應。

在模型中,筆者提取輸入軸(節點1)和太陽輪(節點4)豎直方向的位移響應進行分析,分別采用時域圖、頻域圖、軸心軌跡、相軌跡對比方法,研究健康、轉軸偏心以及偏心-裂紋復合狀態下的系統故障特性。

行星輪系基本參數如表1所示。

表1 行星齒輪基本參數

行星齒輪-轉子系統各個特征頻率如表2所示。

表2 行星齒輪-轉子系統各個特征頻率(單位:Hz)

表2中各個特征頻率計算公式如下[18]:

(20)

式中:fr為輸入軸轉頻;fs為太陽輪轉頻;fc為行星架轉頻;fm為嚙合頻率;fsc為太陽輪故障頻率。

2.1 不同故障條件下系統的動態特性

2.1.1 健康狀況下系統的動態特性

健康狀況下,輸入軸節點1和太陽輪處沿y軸方向振動位移的時間歷程、頻譜、軸心軌跡和相軌跡,如圖7所示。

圖7 健康狀況下系統的振動響應特性圖

由圖7可知:1)健康狀態下,太陽輪(圖7(a)～圖7(d))和輸入軸(圖7(e)～圖7(h))的周期振動主要由時變嚙合剛度激勵引起;2)頻譜中的主要成分為嚙合諧波kfm(k=1,2,3);3)軸心軌跡由于重力影響呈現為偏斜的橢圓形狀;4)相軌跡為單一的封閉曲線,表明系統處于周期運動。

2.1.2 轉軸偏心對系統動態特性的影響

筆者在節點1處設置輸入軸偏心量為10 μm。在轉軸偏心狀態下,輸入軸節點1和太陽輪沿y軸方向振動位移的時間歷程、頻譜、軸心軌跡和相軌跡,如圖8所示。

圖8 轉軸偏心狀況下系統振動響應特性圖

由圖8可知:在輸入軸偏心的影響下,太陽輪和輸入軸的時域幅值明顯增加,時域波形中均存在不平衡激勵引起的大幅低頻振動,以及輪齒嚙合激勵引起的小幅高頻振動;在頻譜圖中,增加了轉頻fr,且其占主要成分,嚙合諧波周邊出現以fr為間隔的邊頻帶,這是由于低頻不平衡振動與高頻嚙合振動相互耦合,引起幅值調制現象,并且轉軸偏心對行星齒輪嚙合振動影響較大。

圖8(c)和圖8(g)中,太陽輪的軸心軌跡表現為向外擴展的偏斜橢圓結構,轉軸軸心軌跡表現為規則的橢圓結構。相軌跡表現為多封閉曲線疊加,系統處于擬周期的運動狀態,轉子偏心故障現象十分明顯。

與正常情況相比,偏心狀態下行星齒輪-轉子系統存在復雜多源耦合振動現象。由于實際行星輪系中轉軸偏心不可避免,故在行星輪系故障特性分析時,不可忽視轉軸偏心的影響。

2.1.3 復合故障對系統動態特性的影響

筆者仍設置輸入軸的偏心量為10 μm,并假設裂紋產生于太陽輪齒根處,筆者根據含裂紋齒輪副時變嚙合剛度模型,沿其擴展路徑,設置損傷程度為40%。

在復合故障狀態下,輸入軸節點1和太陽輪處沿y軸方向振動位移的時間歷程、頻譜、軸心軌跡和相軌跡,如圖9所示。

圖9 復合故障狀況下系統振動響應特性圖

由圖9可知:在偏心-裂紋復合故障的影響下,太陽輪和輸入軸的時域幅值進一步增大,時域波形中出現周期性沖擊成分,這是由于隨著太陽輪旋轉,裂紋輪齒以tsc為周期進入嚙合,對應的嚙合副嚙合剛度降低,引起沖擊性嚙合振動。

時域信號由不平衡振動、正常嚙合振動、故障沖擊振動多源耦合而成,信號成分更加復雜[19-21]。頻譜圖中,除了轉頻fr、嚙合諧波kfm(k=1,2,3…),還出現了復雜的邊帶成分。局部放大后可以看出,主要邊帶頻率成分為kfm±fr以及kfm±fr±nfsc,這是由于低頻不平衡振動及周期性故障沖擊振動對正常的嚙合振動產生了復雜調制。

太陽輪、轉子軸心軌跡呈現為外層分布有周期性沖擊的橢圓形。相軌跡呈現為多曲線混合交錯的紊亂圖形,系統處于復雜運動狀態。

上述故障特性可用于診斷行星輪系偏心-裂紋復合故障。

2.2 裂紋深度對系統動態特性的影響

接下來,筆者將在轉軸偏心量一定的情況下,研究裂紋擴展對系統動態特性的影響。

筆者同樣假設裂紋產生于太陽輪齒根處,并沿含裂紋齒輪副時變嚙合剛度模型中的裂紋路徑,從齒根10%的輕度裂紋損傷開始,逐步加深到40%的中度裂紋損傷,直到損傷程度達到70%時,輪齒瞬間斷裂為止。

偏心狀況下,隨太陽輪裂紋擴展系統振動位移的時域圖和頻譜圖,如圖10所示。

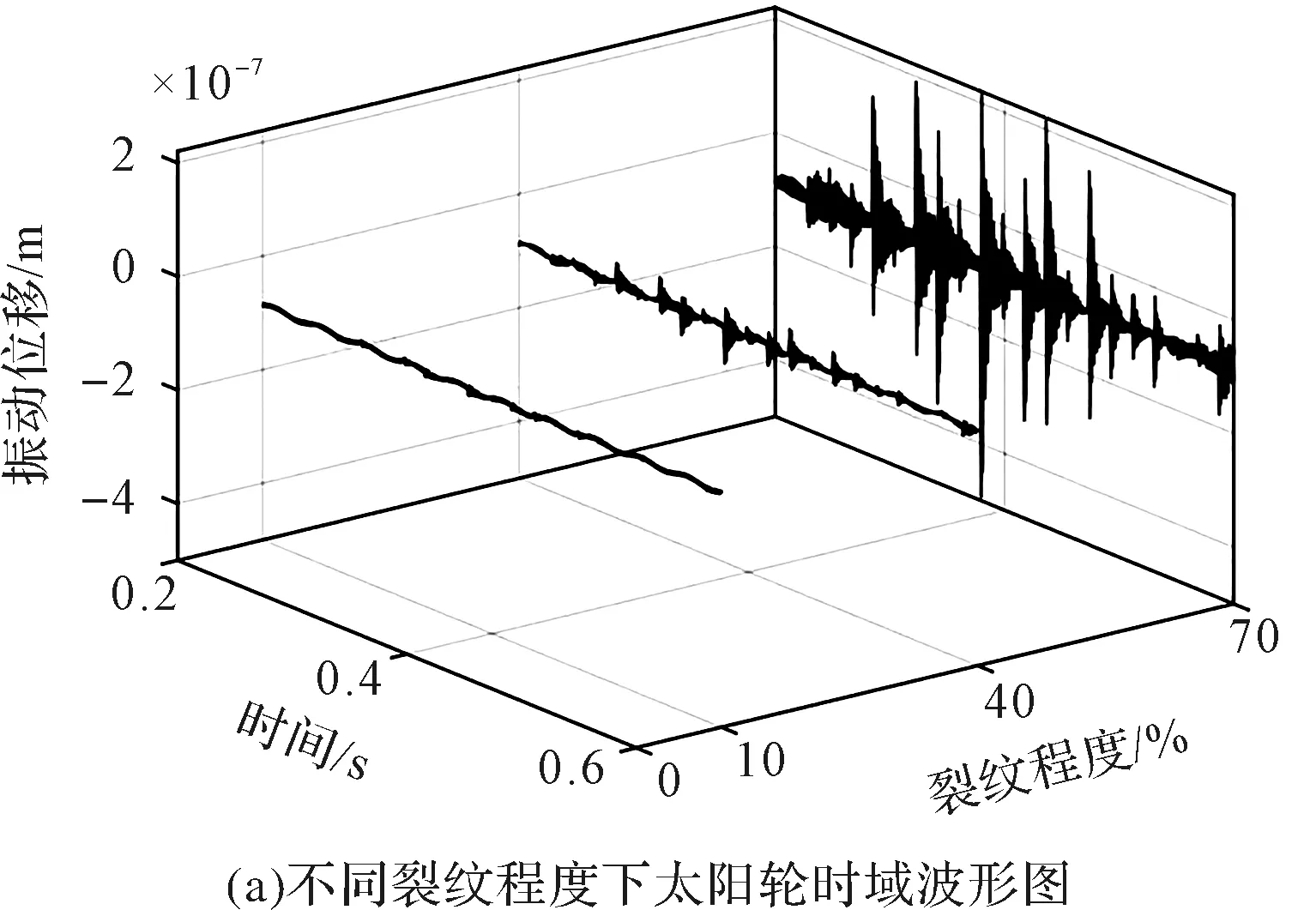
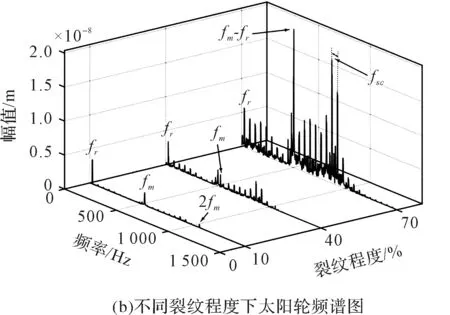
圖10 裂紋擴展下系統振動響應特性圖

從圖10(a)可以看出:當裂紋程度為10%時,轉軸偏心引起的低頻調制非常明顯,早期裂紋引起的故障沖擊十分微弱,且基本被淹沒;隨著裂紋深度增大,裂紋輪齒引起的周期性沖擊逐漸增大。

由圖10(b)可以看出:當裂紋程度為10%時,轉軸偏心產生的低頻成分fr能量較大,嚙合頻率周圍的邊帶成分能量極低;隨著裂紋程度增大,裂紋故障引起的,以fsc為間隔的特征邊頻帶能量逐漸增大。

3 實驗及結果分析

3.1 實驗臺

此處被測齒輪箱為2K-H行星齒輪箱。2K-H行星齒輪箱實驗臺如圖11所示。

圖11 2K-H行星齒輪實驗臺

在2K-H行星齒輪箱中,輸入軸連著太陽輪,輸出軸連著行星架。

筆者采用Dew soft數據采集儀、ZA-21系列電渦流位移傳感器,以及PCB三軸加速度傳感器采集系統振動信號;共布置3個測點,2個加速度傳感器,分別放置在行星齒輪箱的正上方和正側方;位移傳感器共2個探頭,垂直交叉測試行星齒輪箱的輸入軸。

3.2 結果分析

3.2.1 健康狀況下齒輪箱振動響應

不含齒輪故障的行星齒輪箱振動信號如圖12所示。

圖12 無裂紋下實驗臺振動響應信號

由于實際測試中,振動信號會受到強隨機噪聲、多界面傳遞衰減、多振源激勵以及多源誤差激勵的聯合干擾,實測信號成分比仿真信號要更復雜。

圖12(a)和圖12(c)分別為加速度信號及轉軸位移信號的時域波形。從圖中可以看出,波形中存在長周期成分及嚙合高頻振動的相互疊加。

圖12(b)為齒輪箱加速度信號的FFT譜,頻率峰值出現在行星輪嚙合頻率及其倍頻kfm(k=1,2,3…)處,并且嚙合頻率的2倍頻為頻譜圖主頻。由于轉軸的振動經多界面傳遞到齒輪箱箱體,會嚴重衰減,因此,轉頻成分并不明顯;但將嚙合諧波局部放大后,可以發現kfm±fr的邊帶成分。

圖12(d)為轉軸位移信號的頻譜圖,頻率以轉軸的1倍頻fr為主頻。由于嚙合振動位移相對較小,并隨多界面傳遞產生衰減,嚙合頻率成分并不明顯。

綜合上述分析可知:振動響應中同時存在轉軸偏心激勵及嚙合振動激勵,兩種激勵耦合作用下會引起幅值調制現象,使整體呈現出轉軸偏心現象。

3.2.2 輕度裂紋下齒輪箱振動響應

早期太陽輪裂紋故障下的齒輪箱振動信號如圖13所示。

圖13 輕度裂紋下實驗臺振動響應信號

圖13(a)的加速度信號時域波形中出現周期性沖擊成分。

圖13(c)所示的轉軸位移信號時域波形中,以轉軸不平衡引起的長周期波動為主,由于早期裂紋引起的沖擊振動能量較弱,并隨多界面傳遞產生衰減,裂紋引起的沖擊振動并不明顯。

圖13(b)的頻譜圖中,嚙合諧波周邊的邊帶成分更加明顯。由局部放大圖可知,在嚙合頻率fm兩側,存在與轉軸不平衡調制有關的邊帶fm±fr,同時出現了與太陽輪故障特征頻率fsc相關的調制邊帶以及fm±fr±mfsc。

圖13(d)的轉軸位移信號的頻譜中仍是fr占主頻成分。

綜合上述分析可知:在實測故障振動信號中,同時存在轉軸不平衡激勵、嚙合振動激勵以及太陽輪裂紋引起的沖擊等多種激勵耦合作用,形成了復雜的調幅調頻現象,整體呈現出轉軸不平衡-太陽輪裂紋復合故障現象;同時,多源干擾下實測故障信號具有復雜性,需對加速度以及位移傳感信息進行綜合分析,以更準確地判斷系統的故障情況。

3.3 嚴重裂紋下齒輪箱振動響應

嚴重裂紋故障下的齒輪箱振動信號如圖14所示。

圖14 嚴重裂紋實驗臺振動響應信號

隨著損傷程度加大,圖14(a)和圖14(c)振動信號的局部放大波形中,都出現了周期性沖擊成分。裂紋故障程度增大后,頻譜圖中2fm幅值降低,其附近的邊頻帶幅值較圖13(b)明顯增大,這是因為故障產生的沖擊能量明顯增大,而相比之下齒輪嚙合能量占比減小。

圖14(b)的頻譜中,嚙合諧波周圍的邊帶能量增大,調制現象更加明顯。局部放大后,在嚙合頻率fm兩側,fm±fr以及fm±fr±mfsc位置處的峰值明顯。

4 結束語

對于旋轉機械中出現的多源故障問題,筆者建立了含轉軸偏心-齒根裂紋復合故障的行星齒輪-轉子耦合系統動力學模型,以期將該故障模型用于仿真生成行星輪系的故障響應信號。

研究結論如下:

1)根據數值分析得到不同故障條件下,行星齒輪-轉子耦合系統不同節點處的振動信號,采用時間歷程、頻譜、軸心軌跡以及相軌跡綜合分析系統故障特性。結果表明:轉軸偏心會導致低頻不平衡振動與高頻嚙合振動相互耦合,引起幅值調制現象,并且偏心對嚙合振動的影響顯著,在行星輪系故障特性的分析中不可忽視;

2)偏心-裂紋耦合影響下,系統振動響應由不平衡振動、正常嚙合振動、故障沖擊振動多源耦合而成,頻譜中出現轉頻fr、嚙合諧波kfm以及復雜邊帶峰值kfm±fr、kfm±fr±nfsc;并且早期裂紋故障特征微弱,容易被不平衡振動掩蓋。隨著裂紋擴展,故障沖擊及邊帶能量逐漸增大,調制現象更加明顯。

筆者采用不同裂紋故障測試實驗,驗證了模型的準確性。

上述研究可為行星齒輪-轉子系統復合故障診斷提供相關參考。在后續的研究中,筆者將基于實際工況,考慮摩擦潤滑因素,并使用多組實驗進行數據分析,以研究多源因素對行星齒輪傳動系統性能的影響。