用于稀疏孔徑成像系統光程控制的自適應控制算法研究*

錢俊宏,陶 冶,張蓉竹

(1.成都航空職業技術學院 無人機產業學院,四川 成都 610065; 2.四川大學 機械工程學院,四川 成都 610065;3.四川大學 電子信息學院,四川 成都 610065;4.成都凱迪精工科技有限責任公司,四川 成都 610041)

0 引 言

光束干涉成像的3個基本條件是頻率相同、振動方向一致和光程差恒定。但由于受環境變化、大氣干擾或平臺振動等因素的影響,干涉子光束之間會產生較大的光程差,破壞干涉陣列相干成像。因此,想要保證成像質量,就必須對子光束進行實時、快速、高精度的光程調控。

因具有體積小、功耗低、靈敏度高等特點,壓電陶瓷被廣泛應用于納米光學、精密儀器和微電子等高精尖領域的光程調控中[1]。但是,由于壓電陶瓷控制其材料本身存在遲滯非線性,系統的輸出位移會受當前周期與上一個周期的電壓輸入值影響,使一個電壓輸入對應2個或多個位移輸出[2],令系統出現較大的誤差。

對于壓電陶瓷的光程控制方面的研究,最先由美國國家標準局的SCIRE F E和TEAGUE E等人[3]開展的。他們利用壓電陶瓷材料作為驅動執行元件,制作出了一臺壓電微位移平臺。之后,越來越多的國內外高校和科研院所投入到了壓電陶瓷微位移平臺的研究中[4-6]。王芳等人[7]以干涉儀中的壓電陶瓷相移器為執行元件,基于多項式模型,建立了壓電陶瓷遲滯模型,并通過逆模型的前饋控制,實現了微動平臺線性矯正的目的;但其未進行系統累積誤差的分析。趙新龍等人[8]基于Duhem遲滯模型,建立了系統位移—電壓遲滯模型,利用神經網絡系統的擬合,建立了壓電陶瓷遲滯逆模型;但其未進行相應的實際物理實驗。

壓電陶瓷遲滯系統的控制策略研究隨著遲滯模型的發展不斷推進,包括前饋控制、PID控制、復合控制、模糊控制和神經網絡控制等[9]。

陳輝等人[10]基于Duhem遲滯模型,建立了壓電陶瓷遲滯逆模型的數學表達式,以前饋與反饋相結合的方式設計了仿真實驗,證明了該控制方法的有效性;但該研究未進行實際物理實驗。王鈺鋒等人[11]將自適應前饋控制器與PI反饋控制相結合,形成了復合控制系統,提高了系統的泛化能力;但其未將該系統用于光學系統中進行驗證。SVECKO R等人[12]結合前饋神經網絡和BAT搜索算法,成功提高了模型的位置控制精度。CHEN X等人[13]針對遲滯系統存在的不穩定性,提出了一種自適應控制算法,并通過實驗驗證了所提控制方法的有效性;但其未進行幾個系統的聯合控制。

在稀疏孔徑成像系統中,需要用到多個壓電陶瓷,并與成像結果形成閉環校正。目前主要的閉環校正算法有遺傳算法(genetic algorithm,GA)[14]、模擬退火(simulated annealing,SA)算法[15-16]和隨機并行梯度下降(SPGD)算法[17-18]等。

IRINA P等人[19]提出了利用模擬退火算法來校正稀疏孔徑系統的活塞誤差,證明了SA算法在改善系統的點源目標成像質量方面是有效的;但他們只側重于理論分析,未進行相關實際應用實驗。XIE Z等人[20]利用SPGD算法,校正了雙孔徑稀疏孔徑系統中的活塞誤差,驗證了SPGD算法具有收斂速度快、適用性強、精度高的優勢[21];但他們只在實驗室理想環境中,基于光學隔振平臺進行了實驗,并沒有針對實際應用的設備進行實驗。

針對以上問題,筆者對普通PID的微分項和積分項進行改進,形成一種帶濾波器的變速積分PID算法。

筆者將前饋控制與改進PID反饋控制相結合,組成改進的復合控制系統,對單個壓電陶瓷進行控制;搭建單個壓電陶瓷實驗平臺,驗證“前饋-改進PID反饋”復合控制系統的實際性能;在Golay3稀疏孔徑成像系統中,應用SPGD算法完成系統共相誤差的校正。

1 前饋控制

壓電陶瓷在實際使用時,如果直接對其進行控制,則位移—電壓曲線將不會呈現理想的線性關系。在升壓和降壓時,輸出位移存在較大的偏差,并且升壓與降壓時的輸出位移值與期望值都存在差異。這個偏差會給光束的定位和跟蹤帶來誤差,使兩束光到達探測器的時間和角度不同,導致成像質量降低,甚至無法成像。

為了解決這一問題,首先需要獲得壓電陶瓷的遲滯數據。

筆者以德國PI公司生產的S-316.10H壓電陶瓷系統為研究對象,其主要性能參數如表1所示。

表1 S-316.10H性能參數

筆者對該系統施加0 V～150 V的驅動電壓,并間隔10 V,記錄各個電壓值對應的位移變形量;再以10 V電壓為間隔,將外加電壓從150 V降到0 V,記錄對應變形量,得到了電壓與位移對應數據,如表2所示。

表2 電壓與位移對應數據

筆者利用Simulink,將壓電陶瓷遲滯逆模型、壓電陶瓷遲滯模型、壓電陶瓷電容特性以及微動平臺的機械特性串聯起來,完成了前饋控制系統。

為驗證升程與回程2條曲線的控制結果,筆者分別輸入信號y=x與y=40-x;將仿真時間設置為40 s,采樣頻率為20 Hz,得到了前饋控制仿真結果,如圖1所示。

圖1 前饋控制仿真結果

由圖1可知:升程曲線與回程曲線基本為線性,因此,該遲滯逆模型基本能夠消除系統的非線性。在剛開始時位置誤差是比較小的,但在時間為40 s時,升程誤差達到2.5 μm,說明有累計誤差存在。

為了解決這一問題,需要引入反饋控制環節。

2 改進的PID反饋控制

為了提高系統的控制精度、響應速度以及抗干擾性能,筆者分別對PID積分項與微分項進行了改進,提供了一種帶濾波器的變速積分PID算法。

根據系統偏差大小,變速積分可改變積分項的累加速度,從而實現積分項作用與理想PID控制要求相對應的目的:偏差變大時,積分隨之變慢;偏差變小時,積分適當增加。

而在微分控制器中,引入濾波器后,其既能提高系統的動態性能,又能抑制微分項引起的高頻信號干擾。

改進的PID控制器積分項表達式為:

(1)

式中:β為關于系統偏差error(k)的函數。

β表達式設為:

(2)

式中:A,B為人為設定的閾值;β的值可在區間[0,1]內變化,根據系統偏差大小來不斷地調節積分項的強弱。

筆者在PID控制系統微分環節中引入濾波器,PID控制器的結構圖如圖2所示。

圖2 改進的PID控制器結構圖

濾波器可以等效為一個一階慣性環節,一階慣性環節可以過濾高頻信號。其表達式如下:

(3)

式中:Tf為濾波器系數。

PID傳遞函數可由下式表示:

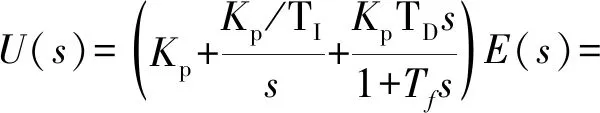
(4)

式中:Kp為比例控制器的比例系數;TI為積分控制器積分常數;TD為微分控制器的微分常數。

微分項表達式為:

(5)

式中:E(s)為系統誤差。

將式(5)改寫成微分方程形式,即:

(6)

離散化:

(7)

將式(7)整理為:

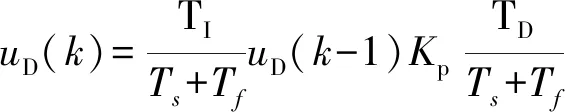
(8)

式中:Ts為系統采樣時間。

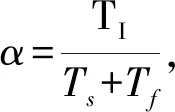
uD(k)=KD(1-α)(error(k)-(error(k-1))+αuD(k-1)

(9)

3 復合控制系統

筆者將遲滯逆模型與改進的PID反饋相結合,形成了復合控制系統。反饋控制器與前饋控制器共同作用于壓電驅動器,其中,遲滯逆模型用于前饋回路中,PID控制器用于反饋,其兼具較快響應與較高精度。

“前饋-改進PID反饋”復合控制系統結構如圖3所示。

圖3 “前饋—改進PID反饋”復合控制結構圖

系統控制器輸出電壓u由2部分組成:即前饋輸出uh與PID控制器輸出uc。

其中,前饋控制環節輸出的補償電壓uh是根據推導出的壓電陶瓷遲滯逆模型Y-1和系統的輸入值y得到的;PID反饋控制輸出的偏差電壓uc是由輸入值和輸出值的偏差量e得到的。

為了驗證改進后的復合控制策略可以有效提高控制效果,筆者分別以階躍信號、斜坡信號和帶干擾的階躍信號為激勵信號,進行了仿真實驗。

實驗過程所用參數值如表3所示。

表3 系統參數值

以階躍信號作為輸入信號時,“前饋-PID反饋”復合控制系統的輸入輸出曲線如圖4所示。

圖4 階躍響應跟蹤仿真

從圖4可知:系統能在0.06 s內達到穩態。由此可見,復合控制系統的控制精度較高,系統響應速度較快。

筆者以斜坡信號作為輸入,令壓電陶瓷系統從0位移到10 μm,速度為5 μm/s,得到了系統的響應曲線和誤差曲線,如圖5所示。

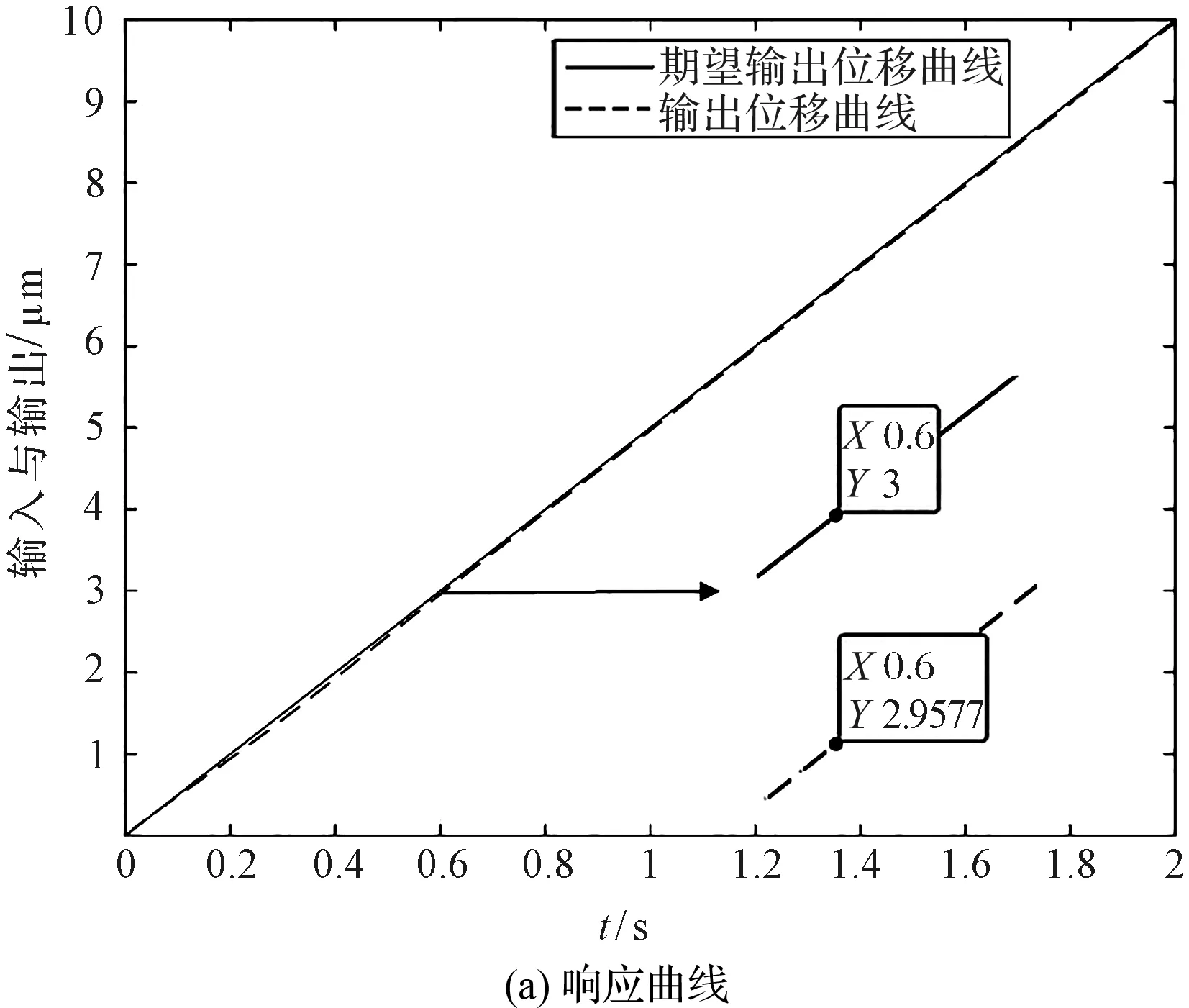
圖5 斜坡響應跟蹤仿真

由圖5可知:“前饋-改進PID反饋”系統在開始跟蹤階段就表現出極穩定的狀態,可以快速跟蹤激勵信號,跟蹤誤差為4 nm。

可見復合控制系統有較好的動態跟隨能力。

當以三角波信號作為輸入信號時,“前饋-PID反饋”復合控制系統的最大誤差為8.7 nm,如圖6所示。

圖6 三角波響應跟蹤仿真

筆者以帶干擾的階躍信號作為輸入(其中,干擾信號幅值為50 nm,頻率為1 kHz),得到了其跟蹤響應曲線(即抗干擾能力仿真結果),如圖7所示。

圖7 抗干擾能力仿真結果

由圖7可知:在加入干擾信號后,“前饋-改進PID反饋”復合系統最大誤差為14 nm。

由此可見,復合控制系統具有較好的抗干擾能力。

4 SPGD聯合控制優化

Golay3稀疏孔徑成像系統中,每一個子孔徑都有一個壓電陶瓷進行光程調控。各子孔徑的光束必須通過一套聯合控制系統進行優化,才能達到校正共相誤差的目的。

館藏資源宣傳：通過多種途徑了解不同類型讀者的信息需求，不斷補充和完善信息資源建設；多種渠道宣傳介紹館藏，使臨床專業人員對館藏資源的知曉率達到90%。

隨機并行梯度下降(SPGD)算法是以成像清晰度為優化目標,采用尋優迭代方法計算各壓電陶瓷的驅動電壓。

SPGD算法的控制過程圖如圖8所示。

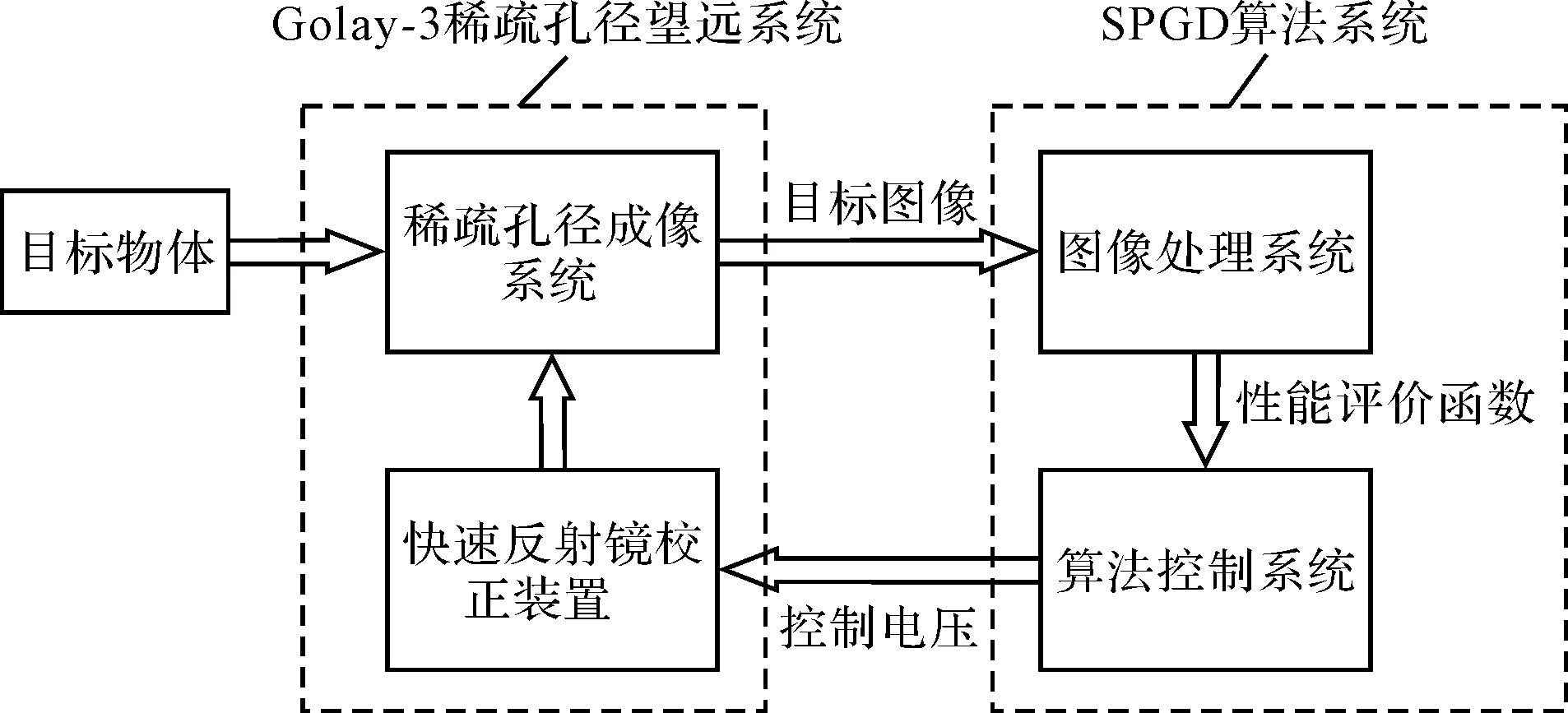
圖8 SPGD算法控制過程

筆者選取歸一化處理的成像面灰度值的平方和作為性能評價函數J,其表達式為:

(10)

式中:(x,y)為成像面坐標;I(xi,yi)為理想圖像灰度值;I(x,y)為實際圖像灰度值。

傳統SPGD算法采用了固定的增益系數與擾動幅值,從而導致其在實際應用中存在迭代速度慢、穩定性低、參數難以實時調節等問題。

針對稀疏孔徑成像系統,筆者在變增益的基礎上,提出了一種自適應增益動量SPGD算法。即通過自適應調節增益系數,并引入梯度的二階動量調控算法,提高了系統的收斂速度和精度;在迭代過程中不斷累積梯度的動量,降低了梯度下降的波動。

算法的迭代公式為:

(11)

mgk=αmg(k-1)+(1-α)gk

(12)

vgk=βmg(k-1)+(1-β)gk2

(13)

(14)

(15)

式中:mgk為梯度一階動量,其初值為0;vgk為梯度二階動量;gk=δuJ為第k次迭代時的梯度估計值;α,β為動量因子。

筆者設置初始增益系數γ0=0.3,隨機擾動δu=0.01 v,且服從伯努利分布[21],活塞誤差為0.5λ,迭代次數為200次,在單色光(λ=633 nm)點源成像條件下,分別應用自適應增益動量SPGD算法以及傳統SPGD算法、文獻[22]提出的變增益SPGD算法和文獻[23]提出的自適應梯度估計SPGD(adaptive gradient estimation stochastic parallel gradient descent,AGESPGD)算法,對Golay-3稀疏孔徑望遠系統單個子孔徑存在共相誤差進行校正。

4種算法的迭代次數k與性能評價函數J的關系如圖9所示。

圖9 不同算法結果

由圖9可知:在迭代200次之后,4種算法均能收斂于極大值,其中,自適應增益動量SPGD算法的收斂速度最快,迭代約90次收斂;AGESPGD算法的收斂速度次之,迭代約150次收斂;變增益SPGD算法迭代約170次收斂;傳統SPGD算法迭代約190次收斂。

5 實 驗

5.1 單個壓電陶瓷位移跟蹤實驗

實驗硬件包括控制模塊、執行模塊和檢測模塊3部分。

系統硬件組成框圖如圖10所示。

圖10 系統硬件組成框圖

S-316.10H壓電陶瓷、固定架、平面反射鏡和裝配后的實物圖,如圖11所示。

圖11 執行模塊硬件

S-316.10H壓電陶瓷內部集成了SGS傳感器作為位置傳感器檢測模塊。SGS傳感器根據壓電陶瓷系統位移量輸出電壓信號;數據采集卡將模擬量信號放大,轉換成數字量輸入運動控制卡進行處理。壓電陶瓷驅動器采用PI公司適配的E-727.3SDA型驅動器。E-727.3SDA是多通道的數字壓電驅動器,可支持3個軸的運動控制,采用D-sub37電壓連接,接口與壓電陶瓷適配。

筆者選用了美國Power UMAC可編程多軸運動控制器,該控制器提供了多種通訊接口,包括串口、網口和USB口,其可以接收來自控制器的模擬量電壓命令,對壓電陶瓷系統進行控制;同時,其可以通過該接口反饋模擬量電壓信號,監視實際到達位置。

控制模塊硬件如圖12所示。

圖12 控制模塊硬件

筆者采用前饋-PID反饋復合控制系統,對壓電陶瓷平臺進行了1 μm、5 μm、8 μm和10 μm位移跟蹤實驗,得到了各位移跟蹤響應曲線和誤差曲線,如圖13所示。

圖13 位移跟蹤響應實驗結果

從圖13中可以看出:系統不同位移的響應曲線都基本與期望位移曲線重合;不同位移的響應時間基本在0.08 s以內,控制誤差在±3 nm以內(只有在行程無限接近或者達到最大行程時,才有明顯的誤差)。

5.2 光程調控成像實驗

稀疏孔徑成像系統的光程調控結構由一個靠壓電陶瓷控制的45°傾斜平面反射鏡,和一個相對固定的45°角錐反射鏡組成,其結構圖如圖14所示。

圖14 光程控制結構圖

筆者將3個光程控制應用于1個三孔徑成像系統中。系統光程調控實驗平臺(光路結構和實驗物理系統)如圖15所示。

圖15 光程調控實驗平臺

3個子孔徑光束需要將Z向誤差控制在λ/10,即55 nm,XY傾斜誤差控制在0.25 μrad范圍內才能在像面干涉成像。在系統的共相誤差校正控制中,單個壓電陶瓷都采用復合控制,3個壓電陶瓷的聯合控制采用SPGD算法進行成像清晰度優化。

筆者利用USAF1951分辨率板作為探測目標,得到了聯合控制前后成像對比結果,如圖16所示。

圖16 光程調控成像實驗結果

筆者采用式(10)的方法,對共相誤差校正前后圖像進行了定量評價:校正前,評價值J1=0.54;校正后,評價值J2=0.78。

從實驗結果可以看出:采用聯合控制系統前,成像結果存在明顯的模糊現象;而采用聯合控制系統后,共相誤差得到了校正,實現了稀疏孔徑系統干涉成像目標。

6 結束語

目前,稀疏孔徑成像系統共相誤差校正存在效果不佳的問題,為此,筆者提出了一種用于光程控制的自適應控制算法。

筆者首先對基于遲滯逆模型的前饋控制進行了仿真,對普通PID進行了改進,并將其與前饋控制組成了前饋-PID反饋的復合控制系統;接著,針對稀疏孔徑成像系統中的多個壓電陶瓷,以成像清晰度作為優化目標,采用一種自適應增益動量SPGD算法進行了聯合控制;然后,對單個壓電陶瓷進行了1 μm、5 μm、8 μm和10 μm位移跟蹤實驗;最后,將SPGD聯合控制系統用于稀疏孔徑成像系統中,進行了分辨率板跟蹤實驗。

研究結果如下:

1)前饋控制仿真表明,遲滯逆模型能夠基本消除系統的非線性特性;但在時間達到40 s,且升程過程中期望位移為40 um時,系統誤差較大;

2)對復合控制系統進行了仿真實驗。當輸入信號為階躍信號時,復合控制系統能在0.06 s內達到穩態;當輸入信號為斜坡信號時,跟蹤誤差為4 nm;當輸入信號為帶干擾的階躍信號時,最大誤差為14 nm;

3)自適應增益動量SPGD算法仿真結果顯示,該算法迭代約90次后達到收斂,明顯比其他3個算法的收斂速度快;

4)單個位移跟蹤實驗結果表明,不同位移的響應曲線都基本與期望位移曲線重合,且響應時間能有效控制在0.08 s以內,跟蹤誤差能有效控制在±3 nm以內;

5)采用SPGD聯合控制系統進行了實驗,系統共相誤差得到了校正,實現了稀疏孔徑系統干涉成像目標。

筆者實現了室內三孔徑系統干涉成像目標,校正了系統內的共相誤差。由于受到系統MTF中頻下降因素的影響,成像清晰度有待提高。因此,后期筆者將針對圖像去噪聲和中頻改善開展進一步的研究。